Droites parallèles, perpendiculaires (d1) ⊥ (d2)

Mathématiques pour la classe de Sixième −Chapitre 5
Droites parallèles, perpendiculaires
Rémi CHEVAL −31 décembre 2014
www.podcast-science.com
Table des matières
1 Les droites remarquables 1
2 Deux constructions importantes 1
2.1 Construire (d′)la droite perpendiculaire à (d)passant par le point A........ 1
2.2 Construire (d′)la droite parallèle à (d)passant par le point A............ 1
3 Vers l’utilisation de trois propriétés 1
3.1 J’ai deux paires de droites perpendiculaires . . . . . . . . . . . . . . . . . . . . . . . . 2
3.2 J’ai deux paires de droites parallèles . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
3.3 J’ai une paire de parallèles et une paire de perpendiculaires . . . . . . . . . . . . . . 2
4 Propriété d’équidistance de la médiatrice 2
1 Les droites remarquables
LES DROITES
REMARQUABLES
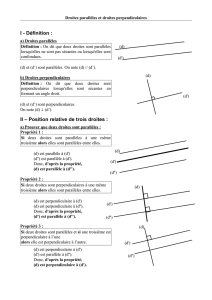
Droites sécantes :
(d1)
(d2)M
●(d1)et (d2)se coupent en M.
●Mest leur seul point d’intersection.
Droites perpendiculaires :
(d1)(d2)
A
(d1)⊥(d2)
●(d1)et (d2)sont perpendiculaires en A
●Elles forment des angles droits.
Droites parallèles :
(d1)(d2)(d1)// (d2)
●(d1)et (d2)sont parallèles.
●Elles ne se couperont jamais.
Médiatrice d’un segment :
(d)A
B
M
●(d)est la médiatrice de [AB]
●(d) est la droite qui coupe (AB) perpen-
diculairement en le milieu de [AB].
2 Deux constructions importantes
Pour les deux constructions qui vont suivre, nous allons utiliser une règle et une équerre.
Les deux côtés de l’équerre
2.1 Construire (d′)la droite perpendiculaire à (d)passant par le point A
A
×
1
2
(d)
(d′)
−Étape 1 : Je place l’un des deux côtés de
mon équerre contre la droite (d).
− Si je déplace mon équerre le long de la droite (d) ,
le deuxième côté de mon équerre me permet de
tracer les droites perpendiculaires à (d).
−Étape 2 : Je trace celle qui passe par A.
2.2 Construire (d′)la droite parallèle à (d)passant par le point A
A
1
2
3
(d)
(d′)
×
−Étape 1 : Je place l’un des deux côtés de
mon équerre contre la droite (d).
−Étape 2 : Je place ma règle contre le
deuxième côté de l’équerre.
− Si je déplace mon équerre le long de la règle, le pre-
mier côté de mon équerre me permet de tracer
les droites parallèles à (d).
−Étape 3 : Je trace celle qui passe par A.
Quelques conseils d’utilisation :
● Avant de vouloir tracer une parallèle (ou une perpendiculaire), il faut identifier deux choses :
●À quelle droite dois-je construire une parallèle (ou une perpendiculaire) ?
●Par quel point doit passer la droite que je souhaite construire ?
● À ce moment là, vous devriez normalement réussir à avoir une idée de l’emplacement de la
droite que vous souhaitez construire. Ne faites jamais une construction à l’aveugle. Ayez
toujours une idée du résultat avant de vous lancer dans la construction.
http://www.podcast-science.com Page 1/3 Sixième - Chapitre 5 - Droites parallèles, perpendiculaires.

3 Vers l’utilisation de trois propriétés
Dans cette nouvelle partie, nous allons découvrir comment utiliser des propriétés mathéma-
tiques pour, à partir de données d’un énoncé, produire une conclusion.
3.1 J’ai deux paires de droites perpendiculaires
−Commence par tracer une droite (d).
−Ensuite trace deux droites (d1)et (d2)per-
pendiculaires à (d).
−On constate que les droites (d1)et (d2)
semblent parallèles.
Situation 1 :
(d1) (d2)
(d)
Propriété 1.
Si deux droites
sont perpendicu-
laires à une même
droite,
Informations
à vérifier
alors ces deux
droites sont paral-
lèles.
Informations
produites
(d1)⊥(d)
(d2)⊥(d)
Données
(d1) // (d2)
Conclusion
3.2 J’ai deux paires de droites parallèles
−Commence par tracer une droite (d).
−Ensuite trace deux droites (d1)et (d2)paral-
lèles à (d).
−On constate que les droites (d1)et (d2)
semblent parallèles.
Situation 2 :
(d1)
(d2)
(d)
Propriété 2.
Si deux droites
sont parallèles à
une même droite,
Informations
à vérifier
alors ces deux
droites sont paral-
lèles.
Informations
produites
(d1) // (d)
(d2) // (d)
Données
(d1) // (d2)
Conclusion
3.3 J’ai une paire de parallèles et une paire de perpendiculaires
−Commence par tracer deux droites (d1)et
(d2)parallèles.
−Ensuite trace une droite (d)perpendiculaire
à(d1).
−On constate que les droites (d)et (d2)
semblent perpendiculaires.
Situation 3 :
(d1)
(d2)
(d)
Propriété 3.
Si deux droites sont pa-
rallèles et qu’une troi-
sième droite est perpen-
diculaire à l’une,
Informations
à vérifier
alors cette 3e
est aussi per-
pendiculaire à
l’autre.
Informations
produites
(d1) // (d2)
(d)⊥(d1)
Données
(d)⊥(d2)
Conclusion
Quelques conseils d’utilisation :
● La question principale est de savoir quelle propriété choisir en fonction de votre
situation. En réalité, et vous allez vous en rendre compte rapidement, le choix est simple.
● Si votre objectif est de démontrer que deux droites sont parallèles et bien, votre choix ne
peut se tourner que vers les propriétés 1 et 2 . À l’inverse, si vous souhaitez des droites
perpendiculaires, vous êtes obligés de vous tourner vers vers la propriété 3.
● Enfin pour choisir entre les propriétés 1et 2, regardez les données que vous proposent votre
énoncé. On parle de droites perpendiculaires Ð→ c’est la propriété 1 . On parle de
droites parallèles Ð→ c’est la propriété 2.
4 Propriété d’équidistance de la médiatrice
Nous allons discuter dans cette dernière section de la propriété d’équidistance de la mé-
diatrice. Voilà, le terme technique est dit et on va faire en sorte qu’il ne nous traumatise pas trop
longtemps.
Théorème (Médiatrice et équidistance).
La médiatrice d’un segment [AB]est
composée de tous les points qui sont
à la même distance de Aet de B.
AM =BM ;AN =BN
AO =BO ;AP =BP
A B
M
N
O
P
http://www.podcast-science.com Page 2/3 Sixième - Chapitre 5 - Droites parallèles, perpendiculaires.

Démonstration de cette propriété d’équidistance (hors-programme)
J’imagine que les plus curieux d’entre vous seront intéressés par des explications supplé-
mentaires concernant cette propriété un peu surprenante. En effet, on peut déjà se poser
la question du pourquoi les points qui sont à égale distance de Aet de Bforment une
droite. Et puis ensuite on se pose la question du pourquoi cette droite est la médiatrice.
Je vous annonce maintenant que nous partons à la recherche d’explications mathéma-
tiques de cette propriété. Comment expliquer que cette impression est bien réelle ?
Comment faire la différence entre une fausse impression et une vérité ?
Sommaire :
●Définir la notion de triangles superposables.
●Présenter deux conditions pour affirmer que deux triangles sont superposables.
●Démontrer que la médiatrice de [AB]est formée de points à égale distance de Aet de B.
●Démontrer que les points à égale distance de Aet de Bsont sur la médiatrice de [AB].
Définition ( Deux triangles superposables). On dit que deux triangles ABC et A′B′C′
sont superposables si on peut superposer leurs représentations géométriques (vous découpez les
deux triangles et vous essayez de les superposer).
A B
C
ab
c
A′B′
C′
a′b′
c′
Dans ce cas, nous avons les informations suivantes :
AB =A′B′;BC =B′C′;AC =A′C′
a=a′;b=b′;c=c′
Le cœur de la notion des triangles superposables se situe dans les conditions qu’il
suffit d’avoir pour affirmer que deux triangles sont superposables.
Condition 1 (Il suffit d’avoir trois égalités de longueurs).
●Si vous avez AB =A′B′, AC =A′C′et BC =B′C′
●Alors vos triangles ABC et A′B′C′sont superposables.
● Vous en avez surement pas conscience mais vous utilisez très
souvent cette condition. En effet quand on vous demande de
tracer un triangle dont vous connaissez les longueurs et
bien, toute le monde tracera des triangles superposables.
● Cette condition explique que les triangles ne sont pas défor-
mables à l’inverse d’un losange que l’on peut transformer en
carré sans toucher à la longueur des côtés.
A B
C
C
5cm
3cm
4cm
Condition 2 (Il suffit d’avoir une égalité d’angles et deux égalités de longueurs).
●Si vous avez AB =A′B′, AC =A′C′et  BAC = B′A′C′
●Alors vos triangles ABC et A′B′C′sont superposables.
● Dans un triangle, si vous connaissez la mesure d’angle et la
longueur des deux côtés adjacents à cet angle, et bien, il
ne vous reste plus beaucoup de liberté pour tracer votre triangle
(voir la figure à droite).
○
○
A B
C
C
5cm
3cm
3cm
1] Tous les points sur la médiatrice de [AB]sont à égale distance de Aet de B.
●Données : M A =MB ;MP =MP ; AMP = BM P = 90
○
●Or la Condition 2 est vérifiée puisque nous avons une égalité
d’angles et deux égalités de longueurs.
●Donc les triangles AMP et BMP sont superposables.
●Donc AP =BP
A B
P
M
2] Tous les points à égale distance de Aet de Bsont sur la médiatrice de [AB].
●Données : AP =BP ;M P =MP ; AMP = BM P =90○
●Or la Condition 2 est vérifiée puisque nous avons une égalité
d’angles et deux égalités de longueurs.
●Donc les triangles AMP et BMP sont superposables.
●Donc AM =BM et donc Pest sur la médiatrice de [AB]
A B
P
M
Extrait du programme officiel
Connaissances Capacités Commentaires
Notions de pa-
rallèle, de per-
pendiculaire
– Tracer, par un point donné, la
perpendiculaire ou la parallèle à
une droite donnée.
–Utiliser différentes méthodes.
– Il est seulement attendu des
élèves qu’ils sachent utiliser en
situation ces notions, notamment
pour la reconnaissance de deux
droites parallèles ou pour leur
tracé.
Médiatrice
d’un segment –
*Connaître et utiliser la défini-
tion de la médiatrice ainsi que la
caractérisation de ses points par
la propriété d’équidistance.
http://www.podcast-science.com Page 3/3 Sixième - Chapitre 5 - Droites parallèles, perpendiculaires.