Exercices Chap 11 P

Page 1 sur 3
Lycée J. CURIE
Terminale S
Année scolaire 2008-2009
Exercices Chap 11 P
mouvements dans le champ de pesanteur
Ex 1 : Pendant son entraînement, un golfeur cherche à envoyer directement la balle dans le trou se trouvant sur le
green. Pour cela, il doit faire passer la balle au dessus d'un petit plan d'eau se trouvant entre lui et le green (voir
figure 1). On néglige tout mouvement de rotation de la balle sur elle-même.
Il fait varier séparément des caractéristiques du vecteur vitesse initiale de la balle.
Dans cette étude la vitesse atteinte par la balle étant faible, on considère comme négligeables les frottements de l'air
dans tout l'exercice. A l'aide de la deuxième loi de Newton, dans le référentiel terrestre supposé galiléen, on peut
établir les équations horaires du mouvement de la balle ainsi que l'équation de sa trajectoire dans le repère (O, x, y).
On appelle portée du lancer la distance D atteinte par la balle lorsqu'elle retombe sur le sol (sur le même plan
horizontal que le point de départ) et flèche du lancer la hauteur maximale H atteinte par la balle pour une abscisse
égale à D/2 (voir figure 1).
On montre que leurs expressions respectives sont :
D =
2
0
2v .cosα.sinα
g
et H =
2
0
v .sin²α
2g
1. Exprimer les coordonnées vox et voy vecteur vitesse initiale
0
v
dans le repère (O ,x, y).
2. Exprimer la portée D et la flèche H en fonction de l'une ou des coordonnées du vecteur vitesse initiale
0
v
.
3. Le golfeur réussit son coup pour un vecteur vitesse initiale
0
v
. Il rejoue maladroitement le coup avec une vitesse
initiale égale à
1
v
(voir figure 2). Exprimer les nouvelles valeurs D1 et H1 de la portée et de la flèche en fonction de D
et H. Dessiner l'allure de la nouvelle trajectoire sur la figure 2.
4. Il rejoue le coup avec une vitesse initiale égale à
2
v
(voir figure 3).
Exprimer les nouvelles valeurs D2 et H2 de la portée et de la flèche en fonction de D et H.
Dessiner l'allure de la nouvelle trajectoire sur la figure 3.
5. Il envoie la balle en conservant le même angle de tir  mais en frappant plus fort. Prévoir qualitativement (sans
calcul) les conséquences sur la portée et la flèche de ce nouveau tir.

Page 2 sur 3
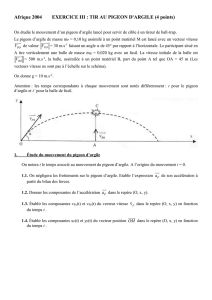
Ex 2 : On étudie le mouvement d’un pigeon
d’argile lancé pour servir de cible à un tireur
de ball-trap.
Le pigeon d’argile de masse mP = 0,10 kg
assimilé à un point matériel M est lancé
avec un vecteur vitesse
PO
V
de valeur
PO
V
= 30 m.s-1 faisant un angle  de 45° par
rapport à l’horizontale. Le participant situé en A tire verticalement une balle de masse mB = 0,020 kg avec un fusil. La
vitesse initiale de la balle est
BO
V
= 500 m.s-1, la balle, assimilée à un point matériel B, part du point A tel que OA = 45
m (Les vecteurs vitesses ne sont pas à l’échelle sur le schéma).
Attention : les temps correspondants à chaque mouvement sont notés différemment : t pour le pigeon d’argile et t’
pour la balle de fusil.
1. Étude du mouvement du pigeon d’argile
On notera t le temps associé au mouvement du pigeon d’argile. A l’origine du mouvement t = 0.
1.1. On négligera les frottements sur le pigeon d’argile. Etablir l’expression
P
a
de son accélération à partir du bilan
des forces.
1.2 Donner les composantes de l’accélération
P
a
dans le repère (O, x, y).
1.3. Établir les composantes vPx(t) et vPy(t) du vecteur vitesse
vP
dans le repère (O, x, y) en fonction du temps t .
1.4. Établir les composantes xP(t) et yP(t) du vecteur position
OM
dans le repère (O, x, y) en fonction du temps t .
1.5. Donner l’équation de la trajectoire du pigeon d’argile.
2. Tir réussi
2.1. Quelle est l’abscisse xC du point d’impact C du pigeon d’argile et de la balle ?
2.2. Vérifier, à partir de l’abscisse xC de l’impact, que le temps de « vol » du pigeon est t = 2,1 s.
2.3. On néglige toutes les forces s’exerçant sur la balle.
2.3.1. Que peut-on dire de son accélération aB ? Que peut-on dire de sa vitesse vB ? Déterminer alors la vitesse vB.
2.3.2. Calculer t’ le temps de « vol » de la balle jusqu’à l’impact connaissant l’ordonnée du point de l’impact yC =
22 m.
2.4. Comparer t et t’ et expliquer pourquoi le tireur peut viser directement le pigeon.
3. Discussion de l’effet du poids de la balle
Dans cette partie l’effet du poids de la balle n’est plus négligé mais on négligera toujours la force de
frottement de l’air.
3.1. Établir que la composante de la vitesse vBy(t’) dans le repère (O,x,y) vérifie l’équation : vBy(t’) = vB0 – g t’.
3.2. Calculer la vitesse vBy au bout d’un temps t’ = 0,044 s, justifier pourquoi on a négligé le poids dans la partie 2
Ex 3 : Un des grands défis de ce siècle (ou du suivant ...) sera d'envoyer une mission d'exploration humaine sur la
planète Mars. Le but de cet exercice est d'étudier quelques uns des nombreux problèmes à résoudre avant de pouvoir
effectuer une telle mission.
On peut imaginer une base relais (pour le matériel comme pour les communications avec la Terre) sur Phobos, un des
satellites de Mars, dont nous allons étudier le mouvement.
On supposera que tous les objets étudiés sont à répartition sphérique de masse.
Données :
Distance entre le centre de Mars et celui de Phobos : r = 9,38.103 km
Masse de Mars : mM = 6,42.1023 kg
La masse de Phobos sera notée mp
Période de rotation de Mars : TM = 24h 37 min
On supposera que Phobos a un mouvement circulaire uniforme autour de Mars de vitesse v et on supposera que l'on
travaille dans un référentiel galiléen centré sur Mars.
1. Donner la définition d'un mouvement circulaire uniforme.
2. Représenter le point d'application, la direction et le sens du vecteur accélération de Phobos sur un schéma.
3. Donner l'expression (sans justification) de la norme du vecteur accélération de Phobos en fonction de v et r.
4. Appliquer la deuxième loi de Newton à ce satellite.
5. En déduire que l'expression de sa vitesse de révolution autour de Mars est: v =
M
Gm
r
.
6. Déterminer l'expression reliant v, r et Tp (Tp étant la période de révolution de Phobos autour de Mars).

Page 3 sur 3
7. Montrer que
2
p
3
T
r
= 9,22.10 -13 s2.m -3
8. En déduire la valeur de Tp.
9. Dans quel plan faut-il placer un satellite pour qu'il soit immobile par rapport à la base relais sur Mars ? Justifier
votre réponse sans calcul.
10. Quelle est la période TS de révolution d'un tel satellite ?
Ex 4 :
On note dans l’exercice mS la masse du satellite S, h son altitude. La Terre possède une répartition de masse à
symétrie sphérique de centre O.
1. Le premier satellite artificiel.
Si la possibilité théorique de mettre un satellite sur orbite autour de la Terre fut signalée en 1687 par Isaac Newton, il
a fallu attendre le 4 octobre 1957 pour voir le lancement du premier satellite artificiel, Spoutnik 1, par les soviétiques.
1.1. Exprimer vectoriellement la force exercée par la Terre sur Spoutnik 1, supposé ponctuel, et la représenter sur un
schéma.
1.2. L'étude se fait dans un référentiel géocentrique considéré comme galiléen. En appliquant la deuxième loi de
Newton établir l'expression vectorielle de l'accélération du satellite.
2. Les satellites artificiels à orbites circulaires.
Le télescope spatial Hubble, qui a permis de nombreuses découvertes en astronomie depuis son lancement en 1990,
est en orbite circulaire à 600 km d'altitude et il effectue un tour complet de la Terre en 100 minutes.
2.1. Étude du mouvement du satellite Hubble dans un référentiel géocentrique
2.1.1 En reprenant les résultats de la partie 1, montrer sans calcul que le mouvement circulaire de Hubble est
uniforme.
2.1.2 Exprimer littéralement sa vitesse en fonction des grandeurs MT, RT, h et G .
2.1.3 Exprimer la période T de son mouvement en fonction des grandeurs précédentes puis retrouver la troisième loi
de Kepler appliquée à ce mouvement circulaire.
2.2. Cas d'un satellite géostationnaire
Les satellites météorologiques comme Météosat sont des appareils d'observation géostationnaires.
2.2.1 Qu'appelle-t-on satellite géostationnaire ?
2.2.2 On propose trois trajectoires hypothétiques de satellite en mouvement circulaire uniforme autour de la Terre.
a. Montrer que, seule, l'une de ces trajectoires est incompatible avec les lois de la mécanique.
b. Quelle est la seule trajectoire qui peut correspondre au satellite géostationnaire ? Justifier la réponse.
3. Les satellites artificiels à orbites elliptiques.
Les satellites peuvent être placés sur différentes orbites, en fonction de leur mission. Un incident lors de leur
satellisation peut modifier l'orbite initialement prévue. Hipparcos, un satellite d'astrométrie lancé par la fusée Ariane
le 8 août 1989, n ‘a jamais atteint son orbite prévue. Un moteur n'ayant pas fonctionné, il est resté sur une orbite
elliptique entre 36 000 km et 500 km d'altitude.
3.1. Les satellites artificiels obéissent aux lois de Kepler.
La deuxième loi de Kepler, dite « loi des aires », précise que « des aires balayées par le rayon, reliant le satellite à
l’astre attracteur, pendant des durées égales, sont égales ».
Énoncer les deux autres lois dans le cas général d'une orbite elliptique.
3.2. Sans souci exagéré d'échelle ni d'exactitude de la courbe mathématique, dessiner l'allure de l'orbite du satellite
Hipparcos. Placer sur ce schéma le centre d'inertie de la Terre et les points A et P correspondant respectivement aux
valeurs 36 000 km et 500 km données dans le texte.
3.3. En appliquant la loi des aires au schéma précédent montrer, sans calcul, que la vitesse d'Hipparcos sur son orbite
n'est pas constante.
3.4. Préciser en quels points de son orbite sa vitesse est maximale, minimale.