101) Une fusée, de masse totale mo =12 t au départ, est lancée

101) Une fusée, de masse totale m
o
=12 t au départ, est lancée verticalement. La propulsion est assurée par un
dispositif à réaction : éjection de gaz chauds produit par la combustion du propergol, à travers une tuyère, avec un
débit massique constant µ = 120 kg.s
-1
à la vitesse relative u
r
par rapport à la fusée (u = 2400 m.s
-1
). Le mélange
combustible a une masse totale m
c
= 0,8.m
o
au départ.
Le champ de pesanteur sera supposé uniforme : g = 10m.s
-2
.
1) En appliquant le principe fondamental de la dynamique :
a) Déterminer la force de poussée exercée par réaction des gaz sur la fusée en fonction de u et µ . A.N .
b) En déduire l'accélération de la fusée ; au départ, au bout de 1 min et de 2 min .
2) Déterminer :
a) L'expression de la vitesse en fonction du temps . Quelle est la vitesse maximale ?
b) Le chemin parcouru par la fusée en fonction du temps . On donne ∫ ln(x)dx=x(ln(x)-1) .
102) Une petite bille de masse m=200g est reliée à deux points A et A' d'un axe vertical ∆ par l'intermédiaire de
deux fils MA et MA' inextensibles et sans masse ; MA=MA'=L=30cm . L'axe ∆ tourne sur lui-même avec une
vitesse angulaire ω =3 π rad.s-
1
.
1) On étudie le phénomène dans le référentiel du laboratoire (O;x,y,z), supposé galiléen ( O milieu de
AA'=2L'=40cm et Oz confondu avec ∆ ) . Pendant l'expérience les deux fils sont tendus . L'accélération de la
pesanteur dans est g=9,81m.s-
2
.
a) Ecrire, dans , l'équation fondamentale de la dynamique appliquée à la bille .
b) Calculer les tensions
T
r
et
'
T
r
des fils MA et MA' .
2) On étudie maintenant le phénomène dans le référentiel (O;x',y',z') mobile par rapport à et dont l'axe Ox'
est confondu avec OM . Déterminer :
a) la force d'inertie d'entrainement,
b) la force d'inertie complémentaire ou de coriolis,
c) l'expression vectorielle de la relation fondamentale de la dynamique appliquée à M dans .
103)
Soit (T;x,y,z) le référentiel géocentrique, supposé galiléen,
et (O;x',y',z') le référentiel du laboratoire lié à la surface de
la terre avec Ox' dirigé vers le sud et Oy' vers l'est .
On étudie le mouvement d'un corps M, de masse 1kg, situé
en un point de latitude Nord λ , par rapport à dans lequel
l'accélération de la pesanteur est g=9,81m.s
-2
. La vitesse
angulaire de la rotation de la terre autour de son axe polaire
est ω
o=7,29.10-
5
rad.s-
1
et le rayon terrestre R=6,35.10
6
m .
1) Si on considère M immobile dans , calculer les forces
d'inerties qui s'exercent sur ce point . A.N : λ =49° .
2.a) Le corps M se déplace sur le plan horizontal Ox'y' avec
une vitesse constante
v
r
(M) =
o
v
r
. Quel est l'effet de la force
d'inertie de Coriolis.
b) On lache, sans vitesse initiale, le corps M d'un point Mo
situé sur Oz' à la distance OMo=h. On suppose que la
verticale est confondue avec l'axe Oz' et que la résistance de
l'air est négligeable. Montrer Que M est dévié vers l'est. Evaluer cette déviation (on négligera les termes en ω ²).
A.N : h=300m , λ =49° .

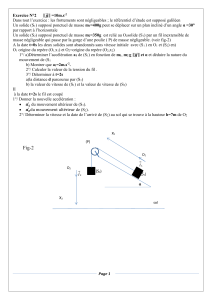
104) La barre AB a une masse m et une longueur 2L . A t = 0, elle
est horizontale, position à partir de laquelle elle est lâchée sans
vitesse initiale . Elle peut pivoter et glisser par rapport au support
horizontal [ O, e z ] . On négligera les dimensions transversales de la
barre et on posera OG(0) = a o .
A partir de quelle valeur α o de α se produit le glissement ? (
coefficient de frottement f en O ) .
105) Une tige mobile AC de résistance R, de masse m, reliée à un
ressort horizontal de raideur k, est posée sur deux rails horizontaux
conducteurs non résistifs . On ne prendra en compte que le frottement
fluide sur la tige v.f
r
r
λ−= . L’ensemble est plongé dans un champ
magnétique uniforme
B
r
vertical.
On donne e(t) =
(
)
tcosE
o
ω . Déterminer, en régime sinusoïdal forcé,
le mouvement de la tige .