Approche graphique Intuitivement, on reconnaît qu

Fonctions continues, théorème des valeurs intermédiaires. C-D 1&2
A Continuité .
Approche graphique
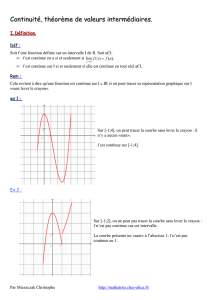
Intuitivement, on reconnaît qu'une fonction est continue sur un intervalle I lorsque sa courbe
représentative peut être tracée sans lever le crayon.
Des exemples :
Les trois premiers graphes présentent des fonctions continues, le dernier
représente une fonction discontinue en deux points, c'est la représentation de la
fonction dérivée de la troisième courbe.
1- Continuité et dérivabilité (admis)
Une fonction qui est dérivable sur I est continue sur I.
Remarque, la réciproque n'est pas vraie, la fonction valeur absolue est continue sur
ℝ
mais
elle n'est pas dérivable sur
ℝ
, elle n'est pas dérivable en 0.
Il existe des fonctions continues sur I mais non dérivable sur I.
2- Continuité des fonctions usuelles
Les fonctions affines, carrées, polynômes, sont dérivables sur
ℝ
donc sont continues sur
leur ensemble de définition.
Les fonctions inverse, rationnelles, racine carrée, valeur absolue sont continues sur tout
intervalle contenu dans leur ensemble de définition .
Les fonctions obtenues par opérations ou composition à partir de fonctions continues sont
continues sur leur ensemble de définition.
,
3- Un contre exemple
La fonction « partie entière » est la fonction définie
sur
ℝ
qui à tout réel x associe l'unique entier
relatif n tel que
nxn1
. On note cette
fonction E.
On a E(3,8) = 3; E(-2,5)=-3; ....
Représentation graphique
S. Baudet 1 sur 4 classe de tle S3

Fonctions continues, théorème des valeurs intermédiaires. C-D 1&2
B Théorème des valeurs intermédiaires
1- Cas général (admis)
Soit f une fonction continue sur un intervalle I.
Si a et b sont deux réels de I et si k est un réel compris entre f(a) et f(b), alors il existe au
moins un réel x compris entre a et b tel que f(x) = k.
(ce théorème est provisoirement admis)
2- Équation
f
(
x
)
=k
.
Soit à résoudre
f
(
x
)
=k
sur I. Si I contient a et b tels que leur images par f encadrent k alors le
TVI assure l'existence d'au moins une solution entre a et b.
Interprétation graphique
Soit C la courbe représentative de la fonction f continue
sur [a ; b] et soit k un réel compris entre f(a) et f(b).
Comme la fonction f est continue, la courbe C traverse la
droite D d'équation
y=k
en au moins un point.
L'équation f(x) = k a donc au moins une solution dans
l'intervalle [a ; b].
Attention : cette solution n'est pas forcément unique.
3- Cas des fonctions continues strictement monotones
Si f est une fonction continue et strictement monotone sur [a ; b], alors pour tout réel k
compris entre f(a) et f(b), l'équation f(x) = k admet une solution unique dans [a ; b].
Démonstration
D'après le théorème des valeurs intermédiaires il existe au
moins un réel x0 tel que
fx0=k
.
Soit x1 un autre réel de [a ; b]; celui-ci est strictement supérieur
ou inférieur à x0, et comme f est strictement monotone
fx1
est strictement supérieur ou inférieur à
fx0
, donc à k.
fx1
ne peut donc pas être égal à k, il n'y a donc pas d'autres
solutions de l'équation f (x) = k dans l'intervalle [a ; b].
Une application
Soit f une fonction continue et strictement monotone sur [a ; b]. Si f (a) et f (b) n'ont pas le même
signe, alors l'équation f (x) = 0 a une solution unique sur [a ; b].
S. Baudet 2 sur 4 classe de tle S3

Fonctions continues, théorème des valeurs intermédiaires. C-D 1&2
4- Convention.
Dans un tableau de variation une flèche indique tout à la fois :
–la stricte monotonie de f si la flèche est oblique
–la continuité de f.
Exemples :
1. f est une fonction définie sur
[
−2;1
]
admet le tableau de variation suivant :
x
-2 -1 0 1
8 3
f
2 -2
Discuter le nombre de solutions de l'équation
f
(
x
)
=4
sur
[
−2;1
]
.
Sur l'intervalle
[
−1;3
]
f admet 3 pour maximum, f n'atteint donc pas 4 sur cet intervalle.
Sur l'intervalle
[
−2;−1
]
f est continue et strictement décroissante
f
(
−1
)
=2
et
f
(
−2
)
=8
, 2 et 8
encadrent 4, alors je peux appliquer le corollaire du TVI et affirmer l'existence d'un unique nombre
compris entre -2 et 1 tel que
f
(
α
)
=4
.
L'équation
f
(
x
)
=4
admet une unique solution sur
[
−2;1
]
.
Remarque. Cette étude affirme le nombre de solution de l'équation mais ne les précise pas.
Ce tableau est celui de la fonction
f
(
x
)
=−2x³+3x²+3
Il convient alors de chercher à approcher la solution
de l'équation
f
(
x
)
=4
à l'aide de la
calculatrice.
Deux méthodes peuvent être observées : par balayage ou par dichotomie....
Par balayage. (voir TD du lundi 24/09)
2. Montrer que l'équation
x3x−3=0
a une solution unique
située entre 1 et 2.
Soit g la fonction définie sur
ℝ
par
gx=x3x−3
. Il s'agit d'une fonction continue. D'autre part,
on a
g'x=3x21
. Comme pour tout réel x on a g'(x)>0, la fonction g est strictement croissante
(donc monotone) sur
ℝ
.
Enfin
g
(
1
)
=−1
et
g
(
2
)
=7
.
Si
x1
, alors
gx−1
et x ne peut pas être solution de
g
(
x
)
=0
.
Si
x2
, alors
gx7
et x ne peut pas être solution de
g
(
x
)
=0
.
Par contre, comme g est continue et strictement croissante sur [1; 2], et comme g(1) et g(2) ont des
signes opposés, il existe un unique réel
situé entre 1 et 2 tel que g(x)=0.
Approche de
...
S. Baudet 3 sur 4 classe de tle S3

Fonctions continues, théorème des valeurs intermédiaires. C-D 1&2
C Compléments au tableau de fonctions dérivées.
1. Fonction
√
u
Soit u une fonction dérivable et strictement positive sur un intervalle I de
ℝ
.
La fonction
f=
√
u:x→
√
u
(
x
)
est dérivable sur I et
f '
(
x
)
=u'
(
x
)
2
√
u
(
x
)
.
Exemple.
f
(
x
)
=
√
4−x2
est définie sur
D=
[
−2;2
]
.
f est de la forme
f=
√
u
avec
u
(
x
)
=4−x2
.
u est dérivable sur
[
−2;2
]
mais
u>0
sur
]
−2;2
[
. Alors f est dérivable sur
I=
]
−2;2
[
et
sur cet intervalle :
f '
(
x
)
=−2x
2
√
4−x2
Important : pour savoir si f est dérivable sur D c'est à dire en -2 et 2 il faut étudier les
limites du taux d'accroissement de f en 2 et en -2.
Remarque : f est paire, sa courbe est symétrique par rapport à (oy) dans un repère
orthonormal, donc si elle est dérivable en 2 elle l'est aussi en -2.
2. Fonction
un
.
Soit Soit u une fonction dérivable et strictement positive sur un intervalle I de
ℝ
.
La fonction
f=un
est définie par
f
(
x
)
=
(
u
(
x
)
)
n
.
Par ailleurs pour tout n, f est dérivable sur I partout où elle est définie et :
f '
(
x
)
=nu'
(
x
)
u
(
x
)
n−1
.
remarque : Si
n<0
, f n'existe pas en les réels x de I tels
u
(
x
)
=0
.
Exemple :
f
(
x
)
=
(
4−x2
)
5
.
f=u⁵
où
u
(
x
)
=4−x²
u est dérivable sur
ℝ
alors f est aussi dérivable sur
ℝ
et :
f '
(
x
)
=5×u'
(
x
)
×
(
u
(
x
)
)
⁴=5×
(
−2x
)
×
(
4−x²
)
⁴=−10 x
(
4−x²
)
⁴
.
Une démonstration par récurrence a été traitée en activité.
3. Fonction
f
(
x
)
=u
(
ax+b
)
f est la fonction définie par
f
(
x
)
=u
(
ax+b
)
où
x→ax+b
est une fonction affine et où u
est une fonction dérivable sur I.
Alors f est dérivable en tout réel x tel que
ax+b∈I
et
f '
(
x
)
=a×u'
(
ax+b
)
.
Exemple
f:x→
√
3x−2
f est du type
f
(
x
)
=u
(
3x−2
)
où u est la fonction racine carrée
dérivable sur
]
0;+∞
[
Alors f est dérivable dès que
3x−2>0⇔x>3
2
et :
f '
(
x
)
=3×1
2
√
3x−2=3
2
√
3x−2
.
S. Baudet 4 sur 4 classe de tle S3
1
/
4
100%