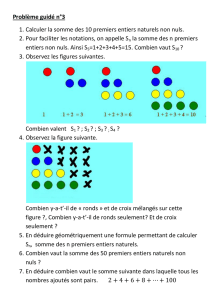
Énoncé Partie I. Partie II.

x(bnxc)n∈N∗
V(x)
M(x)
V(x) = {bnxc, n ∈N∗}, M(x) = {nx, n ∈N∗}
s r
1
s+1 r= 1
V(s)V(r)N∗
j k m j =bkrc=bmsc
j < k +m < j + 1 V(s)∩V(r) = ∅
j∈N∗j /∈V(r)k∈N
kr < j j + 1 ≤(k+ 1)r
j k m
kr < j j + 1 ≤(k+ 1)r ms < j j + 1 ≤(m+ 1)s
k+m < j < k +m+ 1
M(1
r)M(1 s)
j∈N∗
x∈M(1
r)x≤j r,x∈M(1 s)x≤j r
Q
]x∈M(1
r)∪M(1 s)x≤j r=bjsc
M(1
r)∪M(1 s)
(an)n∈N∗
(xn)n∈N∗(yn)n∈N∗
∀n∈N∗,
xn= max nak
k, k ∈J1, nKo
yn= min ak+ 1
k, k ∈J1, nK
(xn)n∈N∗(yn)n∈N∗
(an)n∈N∗
α > 0an=bnαcn∈N∗
xn< ynn∈N∗
xn< ynn∈N∗
(xn)n∈N∗(yn)n∈N∗
α
α an=bnαcn∈N∗
ak= 2k−1k∈N∗

j k m j =bkrc=bmsc
r
s r s
(j < kr < j + 1
j < ms < j + 1 ⇒
j
r< k < j+ 1 r
j
s<m<j+ 1 s
⇒j < k +m < j + 1
1
r+1 s= 1
Nk
mNbkrc=bmscV(r)V(s)
j /∈V(r)
0j
k∈N
bkrc< j < b(k+ 1)rc
bkrckr
j≤ bkrcj kr < j
j
j < b(k+ 1)rc ⇒ j+ 1 ≤ b(k+ 1)rc ≤ (k+ 1)r
j k m
r s r s
k < j
r
m < j
s
⇒k+m<j 
j+ 1
r< k + 1
j+ 1
s< m + 1
⇒j+ 1 < k +m+ 2
k+m < j < k +m+ 1
j∈N∗V(r)V(s)k m
N
N=V(r)∪V(s)
M(1
r)M(1 s)p q
p
r=q s
r
s
1
r+1 s= 1 ⇒1 + r s=r
r
1
r
j
r
kk
r≤j r
j
1
s
j
r
kk
s≤j r⇔k≤sj r
bsj
rc
j+bsj
rc=j+b(j(s−1)cr s
=j+b(js −j)c=j+bjsc − j=bjsc
bx+nc=bxc+n n ∈Z
M(1
r)M(1 s)
W=M(1
r)∪M(1 s) 1 ϕ
N∗W
nNn W ϕ(n)ϕ(n)
j
rn=bjscn=bjrc
ϕ(n)j
sn
bjrc bjscV(s)V(r)N∗
Xn=nak
k, k ∈J1, nKo, Yn=ak+ 1 k, k ∈J1, nK
Xn⊂Xn+1 Yn⊂Yn+1 xn≤xn+1 yn+1 ≤yn

α > 0an=bnαcn∈N∗
∀k∈N∗, ak< kα < ak+ 1 ⇒ak
k< α < ak+ 1 k
Xn
Yn
xn< α < yn
(xn)n∈N∗(yn)n∈N∗
y1
x1x y
n∈N∗
an
n≤xn< yn≤an+ 1 n⇒0< yn−xn<1 n
y=x α
an
n≤xn< yn≤an+ 1 n
xn≤α≤yn
⇒an
n≤α≤an+ 1 n⇒an≤nα ≤an+ 1
α an=bnαc
ak= 2k−1ak
k= 2 −1 k
xn= 2 −1
nnak+1 k= 2
yn= 2 n xn< ynn an