POUR LE JEUDI 13 NOVEMBRE 2008 DEVOIR À LA MAISON N°3

CLASSE DE PREMIÈRE S
POUR LE JEUDI 13 NOVEMBRE 2008
DEVOIR À LA MAISON N°3
I ] CHIMIE. Solutions de chlorure de calcium
Dans cet exercice, les résultats numériques seront donnés avec 3,00 chiffres significatifs.
On dissout : m = 1,665 g de chlorure de calcium, CaCl2, dans de l'eau distillée. Le volume de solution S obtenu est
égal à : V = 250 mL.
1. Écrire l'équation de dissolution.
2. Calculer la concentration massique Cm en soluté apporté dans la solution S.
3. Calculer la concentration molaire volumique C en soluté apporté dans la solution S.
4. Calculer les concentrations molaires volumiques des ions présents dans S.
5. On prélève : V' = 20,0 mL de la solution S, que l'on dilue pour obtenir un volume V1 = 500 mL de solution. Calculer
les concentrations molaires volumiques des ions présents dans la nouvelle solution S1.
6. Comment obtenir, à partir de la solution S, un volume : V2 = 100 mL d'une solution S2 de chlorure de calcium de
concentration molaire en soluté apporté : C2 = 5,99.10-3 mol.L-1 ?
7. Calculer le pourcentage massique de chlorure de calcium dans les solutions S et S1.
On considérera que la densité de toutes les solutions étudiées est égale à 1,00.
On donne : MCa = 40,1 et : MCl = 35,5 g.mol-1.
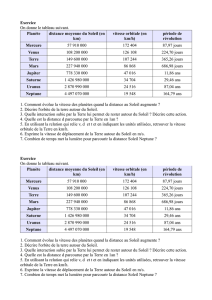
II ] PHYSIQUE. La planète MARS
Voici quelques données concernant la quatrième planète de notre système solaire, Mars.
Le rayon moyen de la planète est de 3 397,2 km ; distance moyenne du Soleil : 1,5237 u.a.
Période orbitale : 686,96 jours ; période de révolution propre : 1,025 957 jours.
Vitesse orbitale moyenne : 24,077 km.s-1 ; 1 jour = 24,0 h.
1. Donner une définition et une valeur numérique pour l'unité astronomique, notée u.a.
2. Exprimer en kilomètres la distance moyenne Soleil-Mars.
3. Quelle est la durée en heures d'un jour martien ?
4. 4.1. Quel mouvement décrit le centre d'inertie de Mars dans le référentiel héliocentrique ?
4.2. Ce mouvement est-il le même dans le référentiel géocentrique ? Justifier.
5. Quelle est la distance parcourue par le centre d'inertie de Mars au cours d'une révolution autour du Soleil ?
6. Retrouver la valeur de la période orbitale à partir de la valeur de la vitesse orbitale moyenne.
7. 7.1. À partir de la valeur de la période de révolution propre, calculer la vitesse angulaire de la planète par rapport à
son axe de rotation.
7.2. En déduire la vitesse (en km.h-1) d'un point situé à la surface de Mars, sur son équateur géographique.
7.3. Comparer cette vitesse à celle, par rapport au référentiel géocentrique, d’un point de l’équateur terrestre,
sachant que le rayon moyen de la Terre est : RT = 6 380 km.
III ] PHYSIQUE. Exercice N° 14 page 63
On notera qu’un système en équilibre sous l’action de trois forces est tel que
les trois forces qu’il subit sont concourantes.