1 Vidange d`un réservoir - PCSI

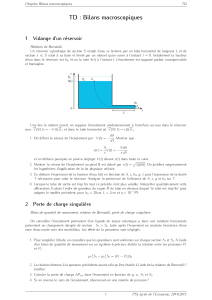
1 Vidange d’un réservoir
1. L’écoulementétantincompressibleethomogène,ledébitvolumiqueseconserveentrelasectiond’entrée
desurfaceSetlasectiondesortiesdutube,d’où:V(t)S=v(t)s.Deplus,lavitessedelasurfacelibre
repéréeparz=h(t)−→ uzestdonnéepardh
dt =−V(t),etdonc:
v(t)=S
sV(t)=−S sdh dt
etcommesS,V(t)v(t)etonpourranégligerV(t)devantv(t)danstoutelasuite.
2. L’écoulementestincompressible,homogèneetparfaitmaisn’estpasstationnaire.Cependantd’aprèsle
résultatdelaquestionprécédentelavitessedevariationdelahauteurd’eaudansleréservoiresttrès
faibledevantlavitessed’éjectiondufluide.Onpeutdoncconsidérerlerégimecommequasi-stationnaire.
OnpeutalorsappliquerlarelationdeBernoullientrelespointsAetB,lelongd’unelignedecourant:
PB
µ+gzB+v2
B
2=PA µ+gzA+v2
A
2
OrPA=PB=P0,za−zB=h,vA=VetvB=v,d’où:
v2−V2=2gh soit v=p2gh puisqueVv
3. Lelienentre dh
dt etv(t)permetd’établirl’équationdifférentiellevérifiéeparh(t):
dh
dt =−V=−s Sv(t)=−s Sp2gh
Séparonslesvariablespourpouvoirfairel’intégrationdecetteéquation:
dh
2√h=−s
Ssg 2dt soit √h−ph0=−s Ssg 2t
LetempsdevidangeTestobtenulorsqueh(T)=0,soitlorsque:
T=S
ss2h0 g
Nouspouvonsvérifierlapertinencedurésultat:Tcroîtsigdiminue(lapesanteurestlemoteurdela
vidange),siSaugmente(ilyadavantaged’eauàévacuer)etsisdiminue(lafinessedutuyaudesortie
limitelavidange).
Lerôledeh0estplussubtilcarh0faitcroîtrelinéairementlevolumed’eauàévacuer,maisfaitcroître
en√h0lavitessed’éjectionv;l’expressiondeTmontrequec’estlepremiereffetquil’emporte,maisle
secondeffetexpliquequeTnesoitpasproportionnelàh0.
4. Silasectionsesttropfaible,lemodèledel’écoulementparfaitn’estpascorrectcarlaviscositéjoueun
rôleimportantdansletubedesortie:nil’équationd’Euler,nilethéorèmedeBernoullinesontvalables
danscecas.
Pour évaluer le rayon Rcritique en dessous duquel la viscosité joue un rôle important, il suffit de
comparerlesforcesvolumiquesdeviscositéintégréessurlalongueurdutubeoùellesinterviennentaux
forcesvolumiquesdepesanteurintégréessurlahauteurh0duréservoir(oncomparealorsdesénergies):
||η∆−→ v||L
||µ−→ g||h0'ηL(v/R2)
µgh0'ηLp2gh0 µgh0R2'ηL√2
µpgh0R2
Lecritèrepourpouvoirnégligerlaviscositéestobtenulorsquelerapportprécédentesttrèspetitdevant
1,soitpour:
RRc=v
u
u
tηL√2
µpgh0'0.12mm
1

2 Perte de charge singulière
1. Systèmeouvert:fluidecomprisentreS1etS2(voirschéma).
Systèmefermé:Σ∗(t)=Σ(t)∪Σ2etΣ∗(t+dt)=Σ(t+dt)∪Σ1.
Bilandequantitédemouvementenrégimestationnaireprojetésurl’axehorizontal:
dp∗
x
dt =δm dt v1−δm dt v2
dp∗
x
dt =µv1S1v1−µv2S2v2
Loidelaquantitédemouvementappliquéeausystèmeferméprojetéesurl’axehorizontal:
dp∗
x
dt =P1S1−P2S2
µS1v2
1−µS2v2 2=P1S1−P2S2
2. Laprésencedezonesd’eauxmortesvientducaractèreréeldel’écoulement.Celuinepeutêtreconsidéré
commeparfaitetdonclarelationdeBernoullinepeutpass’appliquerlelongd’unelignedecourant.
3. Pertedecharge:
∆Ptot =P1+1
2µv2
1−P2+1
2µv2
2
=v2
1µ
2g1−S1 S22
4. Onobserveraitunechutedepressionetnonunemontéedepression,l’originedelapertedechargeétant
unedissipationd’énergiemécanique,c’estuneactionnonconservativequiagitsurlesystème.Pourun
coulementensensinverse,leszonesd’eauxmortesseraientégalementdifférentes.
3 Fusée
1. Lamassedusystèmeconstituédelafuséeetsoncontenuconstituentunsystèmeouvert(So)puisquesa
massem(t)diminueaucoursdutemps.
2. Al’instantt,lesystèmefermé(Sf)correspondàlafuséeetàsoncontenuàl’instantt
Al’instantt+δt,lesystème(Sf)correspondàlafuséeetàsoncontenuàl’instantt+δt etàlamasse
sortiedelafuséeentretett+δt.
3. Lamasseéjectéeentrelesinstanttett+δt vautDmδt donc
m(t)=m0−Dmt
2

4. Al’instantt,laquantitédemouvementdusystèmefermé(Sf)vaut:
−→
pf(t)=m(t)−→ v(t)
Al’instantt+δt,lamasseδm =Dmδt degazéjecté aunevitesse−→ v(t)+−→ u(onremarqueraque
−→
v(t)=v−→ uzet−→ u=−u−→ uz)etdoncunequantitédemouvementDmdt −→ v(t)+−→ u.Lafuséeetson
contenuontunequantitédemouvement−→ p(t+δt)=m(t+δt)−→ v(t+δt)carlecarburant,àl’étatsolide,
possèdelamêmevitessequelafusée.Lesystèmefermé(Sf)adoncpourquantitédemouvementàl’instant
t+δt :−→
pf(t+δt)=m(t+δt)−→ v(t+δt)+Dmdt −→ v(t)+−→ u
Lavariationdelaquantitédemouvemententretett+δt s’écritpourlesystèmefermé(Sf):
D−→ pf=−→ pf(t+δt)−−→ pf(t)=m(t+δt)−→ v(t+δt)+Dmdt −→ v(t)+−→ u−m(t)−→ v(t)
Enlimitantlescalculsàl’ordre1:
D−→ pf=[m(t)−Dmδt]−→ v(t)+d−→ v+Dmdt −→ v(t)+−→ u−m(t)−→ v(t)=m(t)d−→ v+Dm−→ uδt
Endivisantparδt etenpassantàlalimite,nousobtenonsladérivéeparticulairede−→ pf:
D−→ pf
Dt =m(t)d−→
v
dt +Dm−→
u
Lesystèmefermé(Sf)estsoumisàsonpoidsm(t)−→ g.Commel’énoncésupposequelapressionP0est
uniformesurlasurfacedusystème(Sf),larésultantedesforcesdepressionestnulle.Lethéorèmedela
résultantecinétiqueappliquéausystème(Sf)dansleréférentielterrestresupposégaliléens’écrit:
D−→ pf
Dt =m(t)−→
g
Onendéduitfinalement,onutilisantlesdeuxexpressionsde D−→
pf
Dt :
m(t)d−→
v
dt +Dm−→
u=m(t)−→ g
Toutsepassedonccommesilemouvementducentredegravitédelafuséeétaitdécritparl’équation
habituellem−→ a=−→ Fext,àconditiond’ajouterauxforcesréellesuneforcefictive−→ Π =−Dm−→ uappelée
poussée.
5. Enremplaçantl’expressiondem(t)etenséparantlesvariables,onobtient:
d−→ v=−→ gdt −Dm
m0−Dmt−→
udt
quis’intègreen: −→
v(t)=−→ gt +ln(m0−Dmt)−→ u+−−→ cste
Sachantque’àt=0,m(t=0)=m0etv(t=0)=0,onobtient:
−→
v(t)=−→ gt +ln 1−Dmt
m0!−→
u
Cettevitesseestbiendirigéeverslehaut,car−→ uestdirigéverslebas,maisletermelogarithmiqueest
négatif.Onnoteraquecetteformulen’estvalablequ’autoutdébutdumouvement.Eneffet,cellen’esttout
d’abordvérifiéequejusqu’àcequetoutlecarburantsoitépuisé.Danscecas,Dmtepuisement =mcarburant <
m0.Deplus,lorsquelafusées’élève,lagravitéchange,etlapesanteur−→ gn’estplusconstante.
3

4 Jet d’eau de Genève
1. Ledébitvolumiquevaut:DV=πa2
0v0,donc:
v0=DV
πa2
0'56m.s−1
Lahauteurmaximaledujets’obtientenappliquantlethéorèmedel’énergiecinétiqueàunegoutted’eau
(onauraitpuégalementutiliserleprincipefondamentaldeladynamique,maislaméthodechoisieestplus
rapide).Enl’absencedefrottement,toutel’énergiecinétiqueinitialeestconvertieenénergiepotentielle
depesanteur,soit: 1
2mgouttev2
0=mgouttegh.Onendéduitdonc:
h=v2
0
2g'160m
C’estunegrandehauteurpourunjetd’eau,maisvulaphoto,cetordredegrandeurparaîtraisonnable.
2. Ledébitvolumiqueseconservecarl’eauestunfluidequ’onpeutconsidérericicommeincompressible.
Onpeutdoncendéduirelavitessedel’eaudanslagrandecanalisationennégligeantl’influencedela
viscositédel’eausurlaparoi,desortequeleprofildevitessedanslacanalisationestconsidérécomme
uniforme: DV=πa2
0v0=πa2 1v1
Onendéduit:v1=DV
πa2
1'0.6m.s−1.Lavitesseestbeaucoupplusfaiblequ’ensortie,puisquelediamètre
delacanalisationestbeaucoupplusimportant.
Noussommesicidanslesconditionsd’applicationdelaformuledeBernoullipuisquel’écoulementestpar-
fait,incompressible,etpermanent.Lelongd’unelignedecourantentreledébutdelagrandecanalisation
etl’orificedesortie,onpeutdoncécrire:
P0+v2
0
2+gz0=P1+v2
1
2+gz1
orlesdeuxpointsconsidéréssontpresqueàlamêmealtitude,doncz0'z1,etl’eauestàlapression
atmosphériqueP0auniveaudelasortiedujet.Finalement:
P1=P0+µ
2v2
0−v2 1'17.105Pa =17bar
Lapompedoitdoncêtretrèspuissanteafinderéalisercettepression.
3. Effectuonsunbiland’énergiemécaniquepourlesystèmeferméconstitué
– àt:del’eaudanslacanalisationetdel’eauquivarentrerenamontdelapompeentretett+dt,à
lavitesseve≈0,altitudez1;
– àt+dt :del’eaudanslacanalisationetdel’eauquiestsortieparl’orificeentretett+dt,àla
vitessevo,altitudezo≈z1.
L’énergiemécaniquedusystèmeàl’instanttvaut:
E∗
m(t)=Em(t)+DVµdtv2
e
2+megz1≈Em(t)+megz1
L’énergiemécaniquedusystèmeàl’instantt+dt vaut:
E∗
m(t+dt)=Em(t+dt)+DVµdtv2
0
2+mogzo≈Em(t+dt)+DVµdtv2
0
2+megz1
.Enrégimestationaireilyaconservationdudébitmassiqued’oùme≈mo,onfaitdeplusl’approximation
z1≈zo.
Onpeutendéduirelavariationd’énergiecinétiqueentretett+dt ensuivantlesystèmeferméenrégime
stationnaire: dE∗
m=DVµdtv2
0
2
.Appliquonsmaintenantlethéorèmedel’énergiemécaniqueappliquéausystèmefermé:
dE∗
m
dt =Pnc
4

Lesforcesnonconservativessontlesforcesdepression,derésultantenullecarlapressionestsupposée
uniformesurtouteslesfrontièresdusystèmefermé,etl’actiondelapompe.Onendéduitdonc:
dE∗
m
dt =P0
P0=DVµv2
0
2
Applicationnumérique: P0=7,8.105W
.C’estunepuissanceimportante,maislerésultatparaîtraisonnablecar,àtitredecomparaison,unmoteur
depetitevoiturefaitenviron70ch et1ch =736W,soitenviron50kW.Lapuissancerequiseestdonc
celled’unedizainedemoteursdevoiture.
4. Onvérifietoutd’abordbienqueP∞>P0.Ilyadoncunsurplusd’énergiequiaétédissipé.
Appliquonsmaintenantlepremierprincipedelathermodynamiquegénéraliséausystèmeferméprécédent,
afindefaireintervenirdesgrandeursmécaniquesetthermodynamiques.Ilconduitdirectementà:
P1− P0=DVµc∆T
Onendéduitdonc: ∆T=P1− P0
DVµc '0.1˚C
Ladifférencedetempératureestdoncnégligeable.Lefonctionnementdujetd’eaunerisquedoncpasde
réchaufferl’eaudulacetdemettreendangerlaviedespoissons...
5