TD : Bilans macroscopiques - PCSI

Chapitre Bilans macroscopiques TD
TD : Bilans macroscopiques
1 Vidange d’un réservoir
Relation de Bernoulli
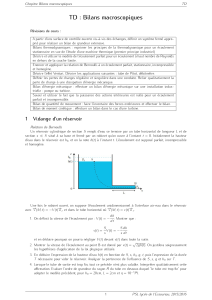
Un réservoir cylindrique de section Srempli d’eau se termine par un tube horizontal de longueur Let de
section sSsitué à sa base et fermé par un robinet qu’on ouvre à l’instant t= 0. Initialement la hauteur
d’eau dans le réservoir est h0, et on la note h(t)à l’instant t. L’écoulement est supposé parfait, incompressible
et homogène.
Une fois le robinet ouvert, on suppose l’écoulement unidimensionnel à l’interface air-eau dans le réservoir
avec −→ v(M, t) = −V(t)−→ uzet dans le tube horizontal où −→ v(M, t) = v(t)−→ ux.
1. On définit la vitesse de l’écoulement par : V(t) = −dh
dt . Montrer que :
v(t) = S
sV(t) = −S s
dh
dt
et en déduire pourquoi on pourra négliger V(t)devant v(t)dans toute la suite.
2. Montrer la vitesse de l’écoulement au point B est donné par v(t) = p2gh(t). On justifera soigneusement
les hypothèses d’application de la loi physique utilisée.
3. En déduire l’expression de la hauteur d’eau h(t)en fonction de S,s,h0,g,t, puis l’expression de la durée
Tnécessaire pour vider le réservoir. Analyser la pertinence de l’influence de S,s,get h0sur T.
4. Lorsque le tube de sortie est trop fin, tout ce précède n’est plus valable. Interpréter qualitativement cette
affirmation. Evaluer l’ordre de grandeur du rayon Rdu tube en dessous duquel "le tube est trop fin" pour
adopter le modèle précédent, pour h0= 20cm,L= 2cm et η= 10−3Pl.
2 Perte de charge singulière
Bilan de quantité de mouvement, relation de Bernoulli, perte de charge singulière.
On considère l’écoulement permanent d’un liquide de masse volumique µdans une conduite horizontale
présentant un changement abrupte de section : S1> S2. Juste après l’évasement on constate l’existence d’une
zone d’eau morte avec des tourbillons. Les effets de la pesanteur sont négligés.
1. Pour simplifier l’étude, on considère que les grandeurs sont uniformes sur chaque section S1et S2. A l’aide
d’un bilan de quantité de mouvement sur un système à préciser, établir la relation entre les pressions P1
et P2:
µv2
1S1−µv2 2S2= (P1−P2)S2
2. La relation obtenue à la question précédente aurait-elle pu être établir à l’aide de la relation de Bernoulli?
Justifier.
3. Calculer la perte de charge ∆Ptot dans l’évasement en fonction de g, v1,S1et S2.
4. Si on inverse le sens de l’écoulement, observerait-on une montée de pression?
1PSI, lycée de l’Essouriau, 2014/2015

Chapitre Bilans macroscopiques TD
3 Fusée
Bilan de quantité de mouvement, cas d’un écoulement non stationnaire
Une fusée en mouvement sur la verticale ascendante dans le réfé-
rentiel terrestre supposé galiléen est soumise au champ de pesanteur
terrestre supposé uniforme.
Elle éjecte des gaz avec un débit massique Dmconstant et une
vitesse relative −→ uconstante par rapport à la fusée et dirigée vers
le bas. On appèlera m(t)la masse de la fusée et de son contenu à
l’instant t. On note −→ vle vecteur-vitesse de la fusée et on suppose
que le carburant y est à l’état solide, et que la fusée est immobile à
t= 0.
1. Justifier pourquoi la fusée et son contenu constituent un système ouvert (So).
2. Faire un schéma d’un système fermé (Sf)que l’on précisera à l’instant tet à l’instant t+δt.
3. Exprimer m(t)en fonction de m0=m(t= 0) (masse de l’ensemble fusée/carburant initialement), Dmet t.
4. En supposant le champ de pression uniforme autour de la fusée, montrer que le mouvement de la fusée
est régi par l’équation :
m(t)d−→
v
dt +Dm−→
u=m(t)−→ g
5. En déduire l’expression de −→ v(t).
4 Jet d’eau de Genève
Bilan d’énergie mécanique, relation de Bernouilli
Le jet d’eau de Genève est alimenté par une grande canalisation de diamètre 2a1= 1m. Le diamètre de
l’orifice de sortie vaut 2a0= 10.7cm et le débit volumique du jet est égal à DV= 500L.s−1.
1. Calculer la vitesse à laquelle l’eau sort de l’orifice. Si l’on néglige tous les frottements, calculer la hauteur
hatteinte par le jet d’eau. Réponses : v= 55,6m.s−1,h= 158m.
2PSI, lycée de l’Essouriau, 2014/2015

Chapitre Bilans macroscopiques TD
2. Calculer la pression P1en aval de la pompe dans la grande canalisation. On considèrera que la sortie
de la pompe et l’orifice de sortie sont à la même altitude. Réponse : P1= 17bar.
3. Avec l’hypothèse que toute la puissance fournie par la pompe est transformée en énergie mécanique,
calculer la puissance P0de la pompe alimentant le jet d’eau. On supposera que la pression au niveau de
la pompe est approximativement celle de l’atmosphère. Réponse :P0≈7,8.105W.
4. La puissance de cette pompe fait en fait P1= 1MW . En admettant que la différence de puissance, due
à des phénomènes dissipatifs, est fournie à l’eau qui circule dans la pompe, calculer la différence de
température ∆Tde l’eau entre la sortie et l’entrée de la pompe. Réponse : ∆T= 0,1˚C.
Donnée :ceau = 4.48.103J.kg−1.K −1
5 Résolution de problème : efforts sur un tuyau coudé
On considère une canalisation coudée de diamètre d et de section constante dans laquelle s’écoule de
l’eau. La canalisation est disposée comme sur le schéma ci-dessous. L’écoulement est stationnaire et considéré
incompressible, homogène et pafait. On néglige tout phénomène de pesanteur. La pression dans la canalisation
en amont de l’écoulement est P1. Le débit volumique dans la canalisation est Dv. La canalisation est en contact
avec l’air extérieur de pression Po.
Données : P1= 6bars,d= 0,20m,Po= 1,0.105Pa.
Il y a rupture de la canalisation si la force qu’elle subit ramenée à sa section est égale à F/S = 16bars.
Calculer le débit volumique maximale dans la canalisation pour que celle-ci ne cède pas.
3PSI, lycée de l’Essouriau, 2014/2015