La réponse à la sélection

Génétique quantitative 2015 – La sélection
La réponse à la sélection
But :
En sélection artificielle : améliorer la valeur d’une population dans une direction désirée
- en choisissant les parents de la prochaine génération
- en contrôlant la manière dont les parents sont recroisés (e.g., en autofécondation,
en allofécondation)
Dans l’étude de population naturelles, comprendre comment la sélection modifie le trait dans
une population, en moyenne et en variance, et découvrir quelles sont les trajectoires
évolutives des populations et comprendre sur quels traits la sélection agit le plus
Prédiction de la valeur des descendants sélectionnés
En utilisant le cadre développé dans les séances précédentes, il faut prédire le changement de
moyenne des descendants à partir de la moyenne des individus sélectionnés.
On appelle R la réponse à la sélection. C’est le changement de moyenne phénotypique
entre la génération parentale et les descendants issus des individus sélectionnés. Lorsque,
par convention, on a centré le phénotype sur zéro dans la génération parentale (phénotype
centré P = Y-µ où µ est la moyenne parentale ; par la suite cette transformation est appliquée
par défaut) , R égale la moyenne phénotypique centrée des descendants (en gardant comme
référentiel la moyenne parentale pour le centrage).
Faire une sélection, quest-ce que c’est ?
Exercer une sélection, c’est faire en sorte que tous les individus de la génération
parentale ne se reproduisent pas de la même façon, en privilégiant la reproduction de ceux qui
ont un certain phénotype (désiré par le sélectionneur). Si l’on veut par exemple augmenter P,
on fera reproduire en priorité les parents ayant une forte valeur de P ; un descendant de cet
épisode de reproduction aura des parents qui en moyenne ont une valeur phénotypique
supérieure que la moyenne de la population de parents (zéro, si on utilise un phénotype
centré). On peut traduire ceci par
Σ Pi wi / Σ wi > 0
Pi est le phenotype de l’individu i, wi est le nombre de descendants qu’il laisse,
contrôlé par le sélectionneur.
ou encore “la moyenne des phenotypes parentaux pondérés par la contribution de
chaque parent à la génération suivante est supérieure à zéro » (la moyenne arithmétique
non pondérée vaut zéro du fait du centrage). Cette moyenne pondérée est appelée différentiel
de sélection, et notée S.
Le moyen le plus couramment utilisé pour sélectionner est d’éliminer une partie des
parents (ceux dont le phénotype est inférieur à une certaine valeur-seuil) avant la
reproduction : seuls se reproduisent ceux qui sont au-dessus du seuil (individus sélectionnés) ;
il s’agit d’une sélection par troncation. Dans ce cas S est simplement la moyenne
phénotypique des parents sélectionnés. On peut la noter aussi
p
PD
, changement de moyenne
phénotypique des parents dû à la sélection.

Génétique quantitative 2015 – La sélection
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••••
•
•••••
•
•••
••
•
•••••
•
•••
••
•
•••
••
•
•••••
•
•••
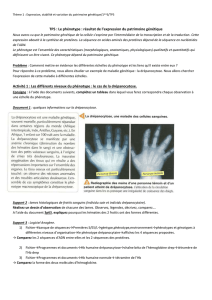
Phénotype du
parent moyen
Phénotype de la descendance
2
hb PO =
Point de
troncation
Différentiel de sélection
S
Réponse espérée
R
Parents sélectionnés
Moyenne des
parents
sélectionnés
Moyenne de la population de parents possibles
S = Σ Pi wi / Σ wi =
p
PD
Que vaut la réponse à la sélection ?
Nous avons vu que la valeur génotypique des enfants Po peut être prédite à partir du
phénotype des parents Pp (midparent value) par la régression suivante
Po= b Pp + e ( Eq. 1)
où la pente de la régression vaut b = cov(Po,Pp)/V(Pp)= h²= V(A)/V(P) dans le cas d’une
reproduction sexuée, d’une espèce diploïde panmictique
Rappelons que dans le cas de lignées ou de clones (sans reproduction sexuée), alors
b= cov(Po,Pp)/V(Pp)= H²= V(G)/V(P). Dans ce cas, les « enfants » sont soit des boutures issues des
parents soit des graines produites par des lignées fixées. Il en va de même pour des organismes
haploïdes.
L’espérance de e est nulle par suite du centrage des variables :
e =Po - b Pp
E(e) = E(Po)- b E(Pp) = 0
De même, la covariance cov(e, Pp) peut s’écrire
= cov(Po - b Pp, Pp) = cov(Po,Pp) – cov(b Pp,Pp) =
= cov(Po,Pp) - b cov(Pp,Pp) = cov(Po,Pp) – cov(Po,Pp) V(Pp)/ V(Pp)
= cov(Po,Pp) - cov(Po,Pp)
=0

Génétique quantitative 2015 – La sélection
Donc e est indépendante de Pp et d’espérance nulle, quelle que soit la distribution
sous-jacente de Pp.
Que vaut la moyenne des descendants issus des parents sélectionnés ?
Les parents sélectionnés ont comme moyenne S=
p
PD
. Leur descendants ont comme moyenne
R (par définition).
En utilisant l’équation 1 :
R = E(Po / parents sélectionnés)
=E(b Pp + e / Parents sel)
= b E( Pp/sélection) + E(e/Parents sel)
= b S + E(e/Parents sel)
La valeur de E(e/Parents sel) représente la moyenne de e chez le sous-ensemble de parents qui
ont été sélectionnés. Cette moyenne est nulle sous certaine conditions : nous avons remarqué
que cov(e, Pp)=0 ; c'est-à-dire que e et Pp sont indépendants. Intuitivement on imagine bien
que en touchant à la moyenne de Pp on ne change pas celle de e (la condition cov( e, Pp)=0
est en fait nécessaire mais pas suffisante, voir remarque ci-après), donc
E(e/Parents sel)=E(e)=0
et
R= b S.
En remplaçant b par sa valeur (en population sexuée panmictique, h²) on obtient
L’« équation du sélectionneur » : R = h² S.
En population asexuée h² doit être remplacée par H².
Remarque : La condition cov(e, Pp)=0 est nécessaire mais pas tout-à-fait suffisante pour que
E(e/Parents sel) = 0. En effet il se pourrait que la relation Pp - Po soit non linéaire; dans ce cas
même si la valeur de b a été choisie pour que cov(e, Pp) =0 (ce qui en fait la meilleure valeur
possible pour une régression linéaire), la moyenne conditionnelle de e sur un certain intervalle
de Pp, en particulier E(e/Parents sel) peut être différente de zéro comme le montre la figure ci-
dessous.

Génétique quantitative 2015 – La sélection
Figure : à gauche, la régression est linéaire, la distribution de e est symétrique avec autant de
positifs (bleu) que de négatifs (jaune), et ce même en restreignant les parents à ceux qui sont-
au dessus du point de troncation T. A droite, la relation est non-linéaire ; sur l’ensemble, il y a
autant de positifs que de négatifs mais au-dessus du point de troncation T il reste une majorité
de positifs donc E(e/Parents sel) >0.
Sous quelles conditions la régression est-elle linéaire ? On ne le sait pas trop, mais on espère
qu’elle l’est à peu près et que sinon l’erreur faite est faible. Si nous supposons que les
phénotypes parentaux et des descendants résultent de l’addition de nombreux effets
génétiques et environnementaux très petits, un théorème mathématique prédit que ces
phénotypes auront une distribution normale bivariée, ce qui garantit la linéarité de la
régression. Mais cela revient en fait à supposer qu’une infinité de gènes porteurs d’allèles à
effet infiniment petit déterminent ce caractère (modèle infinitésimal).
Que se passe t il si la sélection n’est pas faite de manière identique entre les deux sexes ?
(
)
fmfmfm SSSSSSR +=+=+= 2
1
22
2
1
2
2
1hhhbb fm
Traduction de S en intensité absolue de sélection
Cette démarche est nécessaire pour savoir si on applique une plus forte sélection sur l’un ou
l’autre caractère. Comparer S directement n’est pas possible (unités différentes entre les deux
caractères, par ex des mètres et des grammes). Nous devons le standardiser pour obtenir des
échelles comparables d’intensité de sélection i. Cette intensité est définie par :
S = i sp
qui représente le différentiel de sélection « en unités d’écart-type phénotypique ».
Derivation de l’intensité de la sélection
dans une loi normale
0
p
i
z
x
i = z/p
s= 1

Génétique quantitative 2015 – La sélection
. Si x est le point de troncation, alors p est la proportion d’individus sélectionnés et i est
l’intensité de la sélection.
Et le progrès génétique devient :
AP
P
A
PihiihR
ss
s
s
s === 2
2
2
Les valeurs de i sont tabulées.
Relation entre le taux de sélection (p dans le graphe précédent), x point de troncature en unité
d’écart type et i intensité de la sélection
p (%) x i
0.01 3.79 3.96
0.1 3.09 3.36
1 2.43 2.76
2.5 1.96 2.35
10 1.28 1.75
50 0 0.80
Dans une population grande, l’intensité de la sélection varie. Pour des populations inférieures
à 50 individus il faut effectuer une correction.
De même quand la sélection porte indépendamment sur les deux sexes :
(
)
Pfm σhiiR 2
+= 2
1
CPAB3
0
0.5
1
1.5
2
2.5
3
0 20 40 60 80 100
% selected
Selection intensity
Relation entre I et la proportion
d’individus sélectionnés
Grande population