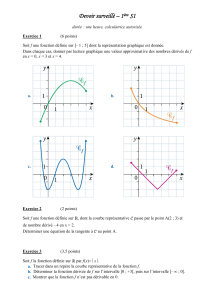
Fonctions strictement croissantes à dérivées qui s

Daniel Saada www.daniel-saada.eu le 3 juin 2009
_______________________________________________________________________________________________
1
09 - FONCTIONS STRICTEMENT CROISSANTES À DÉRIVÉES QUI S’ANNULENT
A) Introduction
Toutes les fonctions de cet article sont à valeurs dans et, sauf au paragraphe E), définies sur . Pour une telle
fonction
f
, on note ()
Z
f l’ensemble 1(0)f−des zéros de
f
; si
f
est dérivable, (')
Z
f est donc l’ensemble des
zéros de '
f
. Quand
f
est de classe 1 C, (')
Z
f est un fermé de , sinon (')
Z
f est un G
δ
1(une intersection
dénombrable d’ouverts) car toute fonction dérivée est limite simple d’une suite de fonctions continues , à savoir
(1/) ()
1/
f
xnfx
n
+− .
Soit
f
dérivable sur . On sait que '0f>implique que
f
croît strictement, mais cette condition n’est pas
nécessaire : la fonction 3
x
x→est strictement croissante sur  et pourtant sa dérivée s’annule en 0x=. Il en de
même si les zéros de '
f
sont isolés : les primitives de |sin( )|
x
sont strictement croissantes sur .
Soit
f
croissante et dérivable sur . Si
f
n’est pas strictement croissante, il existe ab< tels que () ()
f
afb=,
et donc '
f
vaut 0 sur ],[ab : il en résulte que (')
Z
f a la puissance du continu et est d’intérieur non vide. On en
déduit par exemple :
1) La fonction 2
sin (1 / )
x
x→, prolongée par 1/2 en 0x=, ayant une primitive
f
sur (démonstration sur
http://www.daniel-saada.eu/fichiers/10-primitives.pdf),
f
est strictement croissante car sa dérivée ne s’annule
qu’un nombre dénombrable de fois ( bien que 0 soit un point d’accumulation de (')
Z
f).
2) Si F est un fermé d’intérieur vide de , toute primitive
f
de la fonction continue (, )
x
dxF→est strictement
croissante sur  puisque (')
Z
f est exactement F. Un fermé d’intérieur vide s’obtient en prenant le
complémentaire d’un ouvert dense, par exemple ](), ()[
qqrqqrq ∈−+
∪, les réels ()rq étant 0>.
Le but de cette note est de construire une fonction hdérivable et strictement croissante sur 
telle que (')
Z
h soit à la fois dense et de mesure non nulle, donc ni fermé ni dénombrable.
Il en résultera que, h n’étant pas à dérivée continue, (')
Z
hest en outre un G
δ
.
B) Il existe des fonctions
f
dérivables et strictement croissantes telles que (')
Z
f soit de mesure non nulle
mais non dense
Rassemblons les rationnels de en une suite ()
nn
q∈ : l’ouvert ]1/2, 1/2[
nn
nn
qq−+
∪est dense et de mesure
finie, son complémentaire dans est un fermé F d’intérieur vide et de mesure infinie. Si
f
est une primitive de la
fonction (, )
x
dxF→,
f
sera strictement croissante sur ( bien que sa dérivée s’annule un nombre non
dénombrable de fois, Fne pouvant être dénombrable). (')
Z
fF= étant fermé et différent de  ne peut être
dense.
On remarquera que ces fonctions
f
étant 1
Csur , le théorème de Sard assure que ()
f
Fest de mesure nulle
bien que Fne soit pas négligeable, tandis que 1
f
−, continue mais non dérivable, transforme le négligeable
()
f
F en Fde mesure non nulle.
1 On pourra consulter http://books.google.fr/books?id=kq69nXaoV-AC&printsec=frontcover#v=onepage&q&f=false p. 178.

Daniel Saada www.daniel-saada.eu le 3 juin 2009
_______________________________________________________________________________________________
2
C) Il existe une fonction Gdérivable et strictement croissante telle que (')
Z
G soit dense mais de mesure nulle
A la différence des fonctions
f
précédentes, une telle fonction G ne peut être 1 Csur . Nous construirons Gau
moyen de la fonction qui sera sa dérivée, à savoir :
{
}
1/ *
() inf (, ) :
k
k
gx dxE k=∈, où k E est l’ensemble fermé discret
{
}
/2 :
k
pp∈.
Les k
E forment une suite croissante pour la réunion et pour tout
x
, il existe un entier p tel que 1
[, [
22
kk
p
p
x+
∈, d’où
1
(, ) 1/2
k
k
dxE + ≤ . On en déduit d’une part que 01/2g≤≤ , d’autre part que la suite (, )
k
kdxE→ tend vers 0
en décroissant. En élevant (, )
k
dxE à la puissance 1/k, on empêche, comme on le verra, 1/ (, )k
k
dxE de tendre
vers 0 pour tout
x
; nous désignerons par k gla fonction continue 1/
(, )k
k
xdxE→.
La fonction g s’annule évidemment sur 1k
EE
∞
=∪ mais n’est pas identiquement nulle. En effet, soit D
l’ensemble
{
}
/3 : et
n
mm n∈∈ : pour tout /3
n
xm= non entier de D, |/2|32
knk
xp −− −≥ car l’entier
(.2 .3)
kn
mp−ne peut pas être nul (théorème de Gauss) et alors () 1/(2.3) 0
n
gx≥>(n est fixe). Comme E est
dense ( (, ) 0dxE =pour tout
x
), il en résulte que gest discontinue en tout point où elle ne s’annule pas. Ces
discontinuités sont toutes «de deuxième espèce», car il n’y a, par le même argument de densité, ni limite à droite
ni limite à gauche en chaque point de non nullité de g.
Points de continuité de g. Pour t réel, définissons
{
}
{
}
:()gt xgx t≥= ≥ et
{
}
{
}
:()gt xgx t<= <. Chaque
{
}
gt≥étant l’intersection sur l’indice kdes ensembles
{
}
k
gt≥, il en résulte que
{
}
gt≥est fermé pour tout t,
et que
{
}
gt<est donc ouvert, ce qu’on peut vérifier directement puisque
{}
{
}
*
,].2 , .2 [: ,
kk kk
pk
gt p tp t p k
−−
<= − + ∈ ∈
∪.
En particulier, pour tout 0
ε >, il existe donc un réel 0h>tel que
{
}
00 0
], [ ()xhxh ggx ε −+⊂< +. Si 0 ()0gx =,
on a ()gx
ε < sur 00 ], [
x
hx h−+, et comme g est positive, g est continue en 0
x
.
L’ensemble des points de continuité de g est donc ()
Z
g.
()
Z
g est un G
δ
de mesure nulle. La fonction g étant la limite de la suite des fonctions continues 1 min( ,..., )
n
gg,
on en déduit que ()
Z
gest un G
δ
. D’après le théorème de Baire, un G
δ
de ne peut pas se confondre avec la
partie dénombrable dense E qui est un F
σ
(une réunion dénombrable de fermés) : g s’annule donc
nécessairement en dehors de E. Par exemple, si
!
1
1
2
n
n
x
≥
⎛⎞
=⎜⎟
⎝⎠
∑,
()! (1)!
!
1
11
(, ) 2
22
nk n
n
k
dxE
++
∞
=
⎛⎞ ⎛⎞
≤≤
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
∑grâce
à()!(1)!!nk n k+≥++ quand 2k≥ ; on a donc () 0gx = sans que
x
appartienne à E, ce point est facile à vérifier.
Pour établir la négligeabilité de ()
Z
g, il suffit de montrer que pour tout N, () [ , ]
X
Zg NN=∩− est négligeable.
Or
X
est l’intersection des
{
}
[,]:()1/
n
X
xNNgx n=∈− < pour 3n≥. Pour chaque
x
dans n
X
, il existe k tel
que (, ) 1/ k
k
dxE n≤ et donc existe udans k E tel que ||1/
k
x
un−≤ . Ces réels u sont nécessairement dans
[ 1/2 , 1/2 ]
kk
NN−− + et leur nombre est (2 2 / 2 ).2 1 3 2 .2
kk k
NN++=+.Chaque n
X
est donc contenu dans
une réunion double de « boules », d’intervalles en fait, 1(,1/ )
k
ku
B
un
≥
∪∪ ; la mesure de (,1/ )
k
u
B
un
∪est
inférieure ou égale à (3 2 .2 ).2 / 6 / 4 .(2 / )
kk k k
NnnNn+=+. La mesure de n
X
est donc inférieure ou égale à
11
68
6(1/)4.(2/) 12
kk
kk
N
nN n
nn
∞∞
==
+=+
−−
∑∑ : il en résulte que chaque
X
, et par contrecoup ()
Z
g, sont de
mesure nulle.

Daniel Saada www.daniel-saada.eu le 3 juin 2009
_______________________________________________________________________________________________
3
Construction de la fonction G. La fonction gétant mesurable et bornée, elle est intégrable sur tout segment de ,
aussi 0 () x Gx g=∫ est-elle définie pour tout réel
x
(comme la suite des fonctions 1 min( ,..., )
n
gg tend vers gen
décroissant, on a même 1
0
( ) lim min( ,..., )
x
n
n
Gx g g=∫ pour tout
x
, mais cette limite ne sera pas exploitée). Nous
allons prouver que Gest dérivable sur et que sa dérivée est g.
Gest dérivable en tout 0
x
en lequel gs’annule et 00 '( ) ( ) 0Gx gx==. On a vu que pour tout 0 ε >existait un réel
10h>tel que
{
}
11
], [ ()xhxh g gx ε −+⊂< +. Si 1 0hh<< , alors
()()1 1 0()(())()
xh xh
xx
Gx h Gx gxdx gx dx gx
hh h
εε
++
+−
≤=≤+=+
∫∫ .
Quand
x
est un zéro 0
x
de g,0 ()0gx =, il vient immédiatement 0 '( ) 0Gx = à droite ; le lecteur prouvera de
même que 0
'( ) 0Gx = à gauche, ou il invoquera le théorème selon lequel une intégrale est dérivable en tout point
où la fonction qu’on intègre est continue.
Gest dérivable en tout 0
x
en lequel 0
()0gx > et 00
'( ) ( )Gx gx=(bien que g ne soit pas continue en 0
x
).
La démonstration qui suit est due au professeur Jean Saint-Raymond, de l’Université Paris VI.
On se bornera, comme précédemment, à la dérivée à droite.
Fixons
ε
dans 0 ]0, ( )[gx et posons 0 ()tgx ε =− ; les inégalités 0 0 ()1/2tgx<< ≤ induisent 02 1t<< et
1/2 ε <. De plus, pour tout 1k≥,
()
00
(, ) () ( )
kkk
k
dx E gx t t ε ≥=+> et donc, pour tout u de k E, 0 ||
k
x
ut−>.
Pour 0h>, on découpe l’intervalle d’intégration 00
[, ]
x
xh+en la réunion disjointe
{
}
{
}
00 00
[, ] [, ]
x
xh gt xxh gt+∩ ≥+ +∩ <
de sorte que
{}
{}
00
00 00
[, ] [, ]
()()1 1
() ()
xx h gt xx h gt
Gx h Gx g x dx g x dx
hh h
+∩≥ +∩<
+− =+
∫∫
et que
{
}
()
{
}
()
00 00
[, ] [, ]mxx h g t mxx h g t h+∩ ≥ + +∩ < =,
()mA étant la mesure de Lebesgue d’un borélien A de .
Étape 1 : la limite de
{
}
()
00
[, ]mxx h g t
h
+∩ ≥ , quand h positif tend vers 0, est 1.
On va plutôt prouver que
{
}
()
00
0
lim [ , ] / 0
hmxx h g t h
+
→+∩ < =, en utilisant la décomposition
{} { }
00 00
1
[, ] [, ] k
k
x
xh gt xxh g t
∞
=
+∩ <= +∩ <
∪
qui permet de majorer
{
}
()
00
[, ]mxx h g t+∩ < par
{}
()
00
1[, ] k kmxx h g t
∞
=+∩ <
∑
.
L’intersection
{
}
00
[, ] k
x
xh g t+∩ <est l’ensemble des réels x de 00 [, ]
x
xh+pour lesquels existe une graduation u
de k
E telle que ||
k
x
ut−< ; soit k U l’ensemble de ces u. Aucun u de k Un’est 0
x
≤car sinon 0
k
x
uxut−≤−< ,
aussi k
Uest inclus dans 00
], [
k
k
x
xht E++ ∩ et son cardinal majoré par12( )
kk
ht++. Si uest un élément de k U,
l’inégalité 00
||ux ux xx−≤−+− entraîne ()
kk
tth ε +<+, donc
{
}
00
[, ] k
x
xh g t+∩ <
sera vide pour les indices k
tels que ()
kk
ht t ε >+ −. La suite ()
kk
kt t ε →+ −étant décroissante, si ()
qq
ht t ε ≤+ −pour un entier q(ce qui
arrivera nécessairement puisque
()
lim ( ) 0
qq
qtt
ε
+
→+∞ +−=
), alors kq>. Pour un tel h et puisque 01/2t<< :

Daniel Saada www.daniel-saada.eu le 3 juin 2009
_______________________________________________________________________________________________
4
{}
()
{}
()
00 00
1[, ] [, ] 2.(12 2 )
kkkk
kk
kkqkq
mxxh gt mxxh gt t h t
∞
=> >
+∩ < ≤ +∩ < ≤ + +
∑∑∑
, d’où
{}
()
2
00
[, ] 2 2 (2) 2 (2) 4 2 (2)
kkkkk
kq kq kq kq kq
mxx h g t t h t t t h t
>> > >>
+∩ < ≤ + + ≤ +
∑∑∑ ∑∑
, et
{}
()
11
00
42 22
[, ] (2) (2)
112 112
qqqq
hh
mxx h g t t t t t
tt tt
++
+∩ < ≤ + ≤ +
−− −−
.
Soit r assez grand pour que (2 ) (1 2 )
r
tt ε <−et que 1
2
r
t
t
ε
ε
⎛⎞
<<
⎜⎟
+
⎝⎠ et soit 2()/2
r
ht ε =+ .
Si 2
0hh<< , on a, en posant
{
}
max : ( ) / 2
j
qjht ε =∈<+ : qr≥, 1 ()/2
q
ht ε
+
≥+ ,
donc 2
()
qq
tt h
t
ε
εε ε
≤+≤
+, ()
qq
ht t ε ≤+ −, donc
{}
()
00
22
[, ] (2)
112
qq
h
mxx h g t t t
tt
+∩ < ≤ +
−− .
Comme qr≥ et 0
()tgx< :
{}
()
00
22 22 2
[ , ] (2) (1 2)
112 1 12
qr
hh
mxx h g t t t h t
tt tt t
εε
ε
+∩ < ≤ + ≤ + −
−− −+− ,
et enfin
{
}
()
00
00
[, ] 44
22
(1 )( ) ( )(1 ( )
mxx h g t
httgxgx
ε
εε
ε
+∩ < ⎛⎞
≤+ ≤ +
⎜⎟
−+ −
⎝⎠
.
Comme
{
}
()
00
[, ] / 0mxx h g t h+∩ < ≥, on a bien
{
}
()
00
0
lim [ , ] / 0
hmxx h g t h
+
→+∩ < =. On montrerait de même
que
{
}
()
00
0
lim [ , ] / 0
hmx hx g t h
+
→−∩< =(on aurait aussi pu montrer
{
}
()
00
0
lim [ , ] / 2 0
hmx hx h g t h
+
→−+∩< =).
Étape 2 : la limite de 00
()()Gx h Gx
h
+− , quand h positif tend vers 0, est 0
()gx .
Comme get h sont positifs,
{}
{}
00
00
00
[, ]
()()1 () ([ , ] )
xx h gt
Gx h Gx t
gxdx m x x h g t
hh h
+∩≥
+− ≥≥+∩≥
∫
On peut donc affirmer que sur 2
]0, [h,
00
000
()()
( ..) (( ) )(1 .) ( ) (1 .( ))
Gx h Gx t h h gx gx gx
hh
εθ ε εθ ε θ
+− ≥− = +−= −+
et en définitive, 00
0
()()
()10
Gx h Gx gx
h
ε
+− ≥−
car 0 0 ()1/2gx<≤.
Comme il avait été établi que, sur un 1
]0, [h, 00
0
()()
()
Gx h Gx gx
h
ε
+− ≤+
,
12
0min(,)hhh<< implique 00
00
()()
()10 ()
Gx h Gx
gx gx
h
εε
+−
−≤ ≤ +
.
On a bien démontré que la dérivée à droite de Gen 0
x
est 0 ()gx pour tout 0
x
de . Il en est de même de la
dérivée à gauche. La fonction G est donc une primitive de g sur .
En conclusion, Gest croissante sur  car sa dérivée g est positive, strictement croissante car 0g> sur la partie
dense ()D−, tandis que (') ()
Z
GZg=est dense et négligeable.
D) Il existe une fonction hdérivable et strictement croissante telle que (')
Z
h soit dense et de mesure non nulle
L’idée (que m’a communiquée encore Jean Saint-Raymond) est de trouver une fonction dérivable h dont la dérivée
'h est le produit de la fonction g définie en C) par une fonction Fà dérivée continue que nous allons définir :
'.hFg=et donc (') ( ) ()
Z
hZFZg=∪
.

Daniel Saada www.daniel-saada.eu le 3 juin 2009
_______________________________________________________________________________________________
5
En C), nous avons introduit
{
}
/3 : et
n
Dm m n=∈∈ : D est une partie dénombrable, dense du fait de
l'écriture en base trois de tout réel, gne s’annulant pas sur ()D−. Montrons maintenant que dans le
complémentaire de Dexiste un compact K de mesure positive : on entoure chaque point de Dpar un intervalle
ouvert de longueur 1/2n ; la réunion de ces intervalles ouvert est un ouvert dense de mesure finie ; le
complémentaire de cet ouvert est un fermé
X
d'intérieur vide et de mesure infinie. Comme
X
est la réunion
croissante des [,]
X
nn∩− , il existe un entier n tel que le compact [,]KX nn=∩− soit de mesure > 0.
Montrons ensuite qu’il existe une fonction F positive et 1
C sur  telle que ()
Z
FK=. Le complémentaire de K
dans  est un ouvert U, lequel est donc réunion au plus dénombrable d’intervalles ouverts disjoints. L’un de ces
intervalles ouverts est ],[m−∞ où m est le minimum de K, un autre est ], [M+∞ où M est le maximum de K, de
sorte que 1
],[],[ ],[
nn
UmM ab
∞
=−∞ + +∞+
∑, avec ],[], [
nn
ab mM⊂, et que 1 [, ] ] , [
nn
KmM ab
∞
=−
∑. On
définit F sur  en posant
2
2
22
sur
sur ] , [
sur ] , [
sur chaque ] , [.
0 K
()
() ()
()()
nn nn
m
M
ab
xm
Fx xM
xa xb
−∞
+∞
⎧
⎪−
⎪
=⎨−
⎪
⎪−−
⎩
F est évidemment de classe 1
C sur U, positive ou nulle sur , et ()
Z
FK=.
1) F est dérivable sur 
Montrons d’abord qu’il existe une constante C telle que 2
() .(, )Fx CdxK≤ sur . Sur K, les deux membres de
l’inégalité sont nuls ; si
x
m<ou
x
M>, 2 () (, )Fx dxK=. Si nn axb<< ,
{
}
222
(, ) min( ),( )
nn
dxK x a x b=−−
et alors
2
22 2
()
() ( )( ) (, )
4
nn
nn
ba
Fx x a x b dxK
−
=− − ≤ . Comme ],[], [
nn
ab mM⊂, on a 2 () .(, )Fx CdxK≤ pour
tout x si
2
()
max(1, )
4
Mm
C− =. On en déduit que F est dérivable en tout 0
x
de K car 0 |() ()| ()Fx Fx Fx−=
et 22
0
() .(, ) .( )Fx CdxK C x x≤≤− impliquent 0
0
0
() ( ) || Fx Fx Cx x
xx
−≤−
−, F dérivable en 0
x
et 0 '( ) 0Fx =.
F, qui était dérivable sur U, est donc dérivable sur .
2) F est 1
C sur 
Montrons d’abord qu’il existe une constante 'C telle que '( ) '. ( , )Fx CdxK≤sur . Sur K, les deux membres
sont nuls en vertu de a), si
x
m<ou
x
M>, '( ) 2 ( , )Fx dxK=, si nn axb<< , (, ) ( )
n
dxK x a=− ou ()
n
bx−
et 22 2
'( ) 2( )( ) 2( ) ( ) 4( ) . ( , )
nn n n nn
Fx x a x b x a x b b a dxK=− − +− −≤ − : on peut donc prendre
2
'max(2,4( ))CMm=−. Il en résulte que 'Fest continue en tout 0
x
de Kcar quand 0
x
x→, (, )dxKtend vers
0
(,) 0dx K =et 0 | '( ) '( ) | '( ) '. ( , )Fx Fx Fx CdxK−=≤ .
F, qui était de classe 1
C sur U, est donc de classe 1 C sur .
Construction de la fonction h. Puisque .'GF est continue, donc dérivée d’une de ses primitives L, on a
()' ' 'FG F G Fg L Fg=+=+
ce qui montre que Fg est la dérivée de hFGL=−. En conclusion :
3) '.hFg=est positive sur  et ne s’annule identiquement sur aucun intervalle non réduit à un point car g et F
sont 0> sur la partie dense ()D− ;