Notes sur le temps en physique (classique)

1
Notes sur le temps en physique (classique)
Jean-Philippe Uzan
Institut d’Astrophysique de Paris
Titre :
Le sujet imposé par Annick était le temps en cosmologie. Ce qu’un physicien peut
faire, c’est parler du temps dans un cadre théorique donné, c’est-à-dire expliciter la
représentation du temps dans ce cadre, et non chercher à élucider sa nature. Cette tâche
incombe au philosophe.
Le cadre cosmologique devient alors très intéressant. Mais, pour y arriver, je dois
d’abord rappeler la représentation du temps dans le cadre de la physique newtonienne, en
relativité restreinte puis en relativité générale. Nous finirons par le contexte des modèles
cosmologiques développés dans le cadre de la théorie de la relativité générale. Mon exposé se
restreint au contexte classique et ne tiendra pas compte de ce que nous dit la mécanique
quantique….simplement par manque de temps !
Ces notes qui reprennent les grandes lignes de mon exposé ne doivent surtout pas être
considérées comme un texte rédigé.
Remarques préliminaires :
Avant de commencer, je dois faire quelques remarques d’ordre général.
1- En feuilletant dictionnaires et encyclopédies, il semble que nous n’ayons
pas de définition non tautologique du temps. Par exemple, celle de Giono,
le temps est ce qui passe quand rien ne se passe est circulaire. D’une
certaine façon, Saint-Augustin avait déjà résumé la situation dans laquelle
nous nous trouvons, Le mot temps ne nous dit rien de la chose qu’il
désigne.
2- Dans le langage courant, ce mot a de nombreux sens :
succession/simultanéité/durée/changement/époque/devenir/attente/…
Ceci risque de compliquer la discussion scientifique car nous allons devoir
distinguer ces différents concepts.
3- En physique, il y a deux débats distincts autour du temps. Le premier
concerne le cours du temps, c.-à-d. la façon d’ordonner les événements
causalement reliés. Le second concerne la flèche du temps. Ce problème
semble surtout être une propriété des phénomènes temporels et non du
temps lui-même. En effet, les lois de la physique microscopique sont
invariantes sous un échange du sens de l’écoulement du temps mais la
nature nous offre de nombreux phénomènes irréversibles. La flèche du
temps est une propriété de ces phénomènes.
4- En science en général, il semble y avoir une confusion entre le temps lui-
même et les phénomènes temporels (on parle du temps géologique, du
temps biologique etc. pour désigner le temps ou plutôt l’échelle de temps

2
des phénomènes géologiques ou biologiques). En particulier, la
représentation (et la mesure du temps) se fait à travers une spatialisation.
5- Le lien entre le temps et le mouvement devra être clarifié. En particulier, le
temps est souvent spatialisé en physique.
Le temps et sa mesure dans la physique classique :
On peut presque dater l’apparition du temps dans la formulation des lois de la
physique (mais je prends plein de bémols car je ne suis pas historien). Elle se fait avec l’étude
du mouvement. La science grecque classique s’était principalement intéressée à la statique et
la compréhension des lois du mouvement était assez limitée. Commençons par rappeler
comment la mesure du temps a évolué.
Les principaux outils dont on disposait étaient des clepsydres, des sabliers, des bougies
graduées et des cadrans solaires. Ces derniers permettaient de mesurer le temps sur de longues
durées mais en un endroit fixe et avec une faible précision (au mieux 5 à 10 minutes). Les
clepsydres et les sabliers pouvaient être précis mais étaient souvent restreints à la mesure de
petits temps et devenaient peu précis sur de longues périodes (il faut retourner le sablier, etc.
ce qui entraîne une dérive non régulière). Les bougies étaient peu précises et ne permettaient
pas de mesures reproductibles (chaque bougie étant différente). Les horloges apparaissent dès
le XIVème siècle mais n’indiquent alors que les heures.
En 1583, Galilée réalise que les pendules permettent de mesurer le temps avec une
bonne précision. Il dessina un projet d’horloge à pendule mais elle ne fut jamais construite et
c’est Christiaan Huygens et Salomon Coster qui réalisèrent la première horloge de ce type en
1657. Les premières horloges « précises » et stables apparaissent au XVIIIème siècle,
principalement sous l’élan de John Harrisson (1734).
Une horloge doit permettre de définir des intervalles de temps réguliers. Un problème
semble cependant apparaître car comment savoir que les intervalles de temps donnés par
l’horloge sont réguliers si on ne possède pas déjà une horloge ? Expliquons comment
construire une horloge même si on ne possède pas un phénomène physique régulier.
Supposons que nous disposions de deux objets (des clepsydres par exemple) qui peuvent ne
pas être identiques et que nous voulions les graduer pour en faire des horloges. La seule
hypothèse importante est que les phénomènes étudiés soient reproductibles (c'est-à-dire que,
pour chaque clepsydre, si la situation initiale est identique alors l’écoulement est identique).
Pour obtenir la première graduation, on fait débuter l’écoulement des deux clepsydres en
même temps et on les arrête, arbitrairement, en même temps. On obtient ainsi une première
graduation, notre unité de temps, qui est arbitraire. Pour obtenir la seconde graduation, on
remplit une des deux clepsydres et on fait repartir l’écoulement des deux clepsydres en même
temps jusqu’à ce que le niveau de la première atteigne la première graduation. On arrête alors
l’écoulement dans les deux clepsydres. On marque alors une deuxième graduation sur la
seconde clepsydre. On peut continuer ainsi pour obtenir une clepsydre graduée régulièrement
même si l’écoulement de l’eau n’est pas régulier.
On voit ainsi que l’on peut fabriquer des horloges régulières à partir de phénomènes
non réguliers pour peu que ces phénomènes soient reproductibles, c.-à-d. que le phénomène
ne dépende pas de l’instant dans le temps où il est initié. Il s’agit là d’une hypothèse forte de
la physique : les lois physiques recherchées sont universelles, et ne dépendent pas du lieu où
de l’époque. Dans la construction précédente, le temps est assimilé à la notion de durée.

3
Revenons au concept de temps en physique. On peut dater son introduction à 1604
(date reconstruite par divers historiens). C’est à cette époque que Galilée formule la loi de la
chute des corps qui fait intervenir pour la première fois explicitement le paramètre temps (les
vitesses de chute sont proportionnelles aux temps de chute).
La formalisation du temps sera ensuite effectuée par Newton dès l’ouverture des
Principia (1687) :
« Absolute, true, and mathematical time, of itself and of its own nature, flows equably
without relate onto anything external, and by an other name is called duration »
Cette définition nous renvoie à l’image de la rivière d’Héraclite. Le temps coule de façon
inexorable. Il peut être décrit par une variable continue à une dimension. Ces hypothèses ne
laissent que deux possibilités car les espaces à une dimension sont de deux types : les boucles
et les lignes infinies.
La physique invoque un autre principe, qui en soit est une lapalissade si on essaie de
comprendre les lois de la nature. Il s’agit du principe de causalité, qui stipule que « les causes
précèdent les effets ». On peut le reformuler en « les effets ne peuvent pas rétroagir sur leurs
causes ». Dans le cadre newtonien, cela implique que le temps ne peut pas être cyclique si
bien qu’il doit être linéaire. On en déduit donc que dans ce cadre, les voyages dans le temps
sont strictement interdits. Remarquons tout de même ici que nous ne devons pas être
impressionnés par les mots : comment distinguer une cause d’un effet ? Pour cette raison, le
principe de causalité est un concept qu’il faudra élucider et non une hypothèse à utiliser telle
qu’elle.
Dans le cadre Newtonien, le temps est donc linéaire et il « coule » inexorablement de
façon régulière, « en solitaire ». On peut donc représenter l’espace et le temps de la physique
classique comme un cristal à trois dimensions comportant une horloge en chaque point.
Toutes les horloges étant synchronisées, par construction. Le temps est aussi indépendant du
mouvement des observateurs si bien que la montre d’un tel observateur synchronisée avec une
des horloges le sera avec toutes les autres et pour toujours. Le temps mesuré par deux
voyageurs entre deux rencontres ne dépend pas de leurs chemins respectifs. Soulignons aussi
que dans ce cadre, le temps est découplé du concept de mouvement ; ce n’est pas parce que
rien ne bouge que le temps n’existe plus.
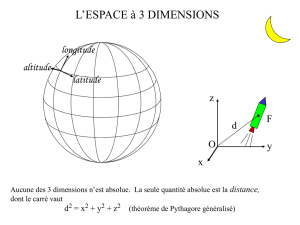
Une autre façon de représenter cette structure est de considérer un « film d’espaces »,
c.-à-d. une succession d’espaces à divers temps (voir la figure 1). L’espace-temps est alors
une entité à 4 dimensions car il faut 4 nombres pour repérer tout événement, sa position
spatiale et le temps où cet événement a lieu.
Pour tout événement P, il existe une notion intuitive de simultanéité. Si l’on considère
un second événement Q, alors il y a trois cas de figures : (1) on peut aller de P à Q, Q
appartient alors au futur de P, (2) on peut aller de Q à P, alors Q appartient au passé de P, (3)
il est impossible de voyager entre P et Q, les deux événements sont alors simultanés. Cette
structure repose donc sur la possibilité, en principe, de voyager à n’importe quelle vitesse
finie.

4
Fig. 1 : la représentation du temps en physique classique. L’espace-temps possède quatre
dimensions et peut être visualisé comme un cristal d’horloges synchronisées (gauche) ou
comme un feuilletage d’espace (droite).
La dynamique classique a été établie par Galilée et Newton avec l’introduction des
notions de vitesse et d’accélération. L’idée révolutionnaire consistait à réaliser qu’une force
modifie l’accélération et non pas la vitesse. Un corps libre se déplace donc à vitesse constante
(contrairement à la physique d’Aristote). Une conséquence de ce principe d’inertie est qu’il
est impossible de distinguer un mouvement à vitesse constante par rapport à l’espace absolu
d’une situation de repos, c’est ce que l’on appelle le principe de relativité galiléenne. Ces
référentiels sont appelés référentiels inertiels et forme une classe privilégiée de référentiel. En
particulier, la cinématique galiléenne est caractérisée par la propriété d’addition des vitesses :
un observateur se déplaçant à la vitesse U par rapport à un référentiel fixe observera la vitesse
V d’un mobile par rapport à ce même référentiel comme V-U.
Dans ce cadre, l’état de tout système dont les positions et vitesses sont connus à un
instant initial, peut être caractérisé à un instant final. La loi de la dynamique reliant
l’accélération à la force est cependant invariante si l’on remplace t par –t si bien que le sens
d’écoulement du temps est arbitraire et n’affecte pas la dynamique. En particulier, n’importe
quel système peut retrouver dans son futur un état physique qu’il a connu dans le passé (c’est
ce que l’on appelle le Théorème de récurrence de Poincaré). Ceci n’implique cependant pas
que l’on est revenu dans le passé. Les phénomènes physiques irréversibles ne satisfont pas
cette propriété.
Une dernière remarque concerne la notion d’énergie. Pour un système mécanique en
mouvement, il existe des fonctions des grandeurs cinématiques (vitesses, positions) qui
conservent une valeur constante pendant le mouvement. Ces constantes du mouvement, aussi
appelées intégrales premières du mouvement, sont reliées aux constantes arbitraires qui
apparaissent dans la résolution des équations du mouvement. Pour un système de N particules,
on a N positions et N vitesses si bien qu’il apparaît 2N constantes arbitraires dans la solution.
Une de ces constantes peut être supprimée car l’origine des temps est arbitraire.
Certaines des intégrales premières du mouvement ont une origine très profonde, liée
aux propriétés de l’espace et du temps. On peut montrer que l’uniformité du temps, c.-à-d. la
propriété que les lois de la physique sont les mêmes à tout temps (ce qui implique entre autre
que le temps n’apparaît pas explicitement dans ces lois), implique que l’énergie est conservée.

5
Le temps de la relativité restreinte :
La cinématique a été remise en cause à la fin du XIXème siècle principalement parce qu’elle
était en contradiction avec les lois de l’électromagnétisme développées par James Clerck
Maxwell. Le point central autour duquel s’est construite la relativité restreinte est la
propagation de la lumière
Pour concilier la cinématique classique, la théorie de Maxwell et les résultats de
l’expérience de Michelson-Morley, trois solutions s’offraient :
1- admettre que les postulats de la théorie de Maxwell n’étaient pas corrects,
2- rendre compatible les postulats des deux théories,
3- admettre que les postulats de la cinématique classique n’étaient pas corrects.
La première solution se révéla rapidement inacceptable. La deuxième solution conduit à
l’introduction du concept d’éther déterminant un référentiel privilégié servant de support à la
propagation des ondes électromagnétiques. Cependant toutes les expériences tentant de mettre
ce milieu en évidence ont échoué. La troisième solution se trouva être la bonne voie et mena,
avec différentes étapes que nous ne détaillerons pas ici, à la formulation de la relativité
restreinte, qui supplanta la cinématique galiléenne. Cette théorie est basée sur deux postulats :
Premier postulat : tous les référentiels d’inertie sont équivalents.
Second postulat : la vitesse de la lumière dans le vide est indépendante de l’état de
mouvement de la source.
Le premier postulat renforce le principe de relativité galiléenne et implique que les lois
physiques prennent la même forme dans tous les référentiels d’inertie. Le second est en
contradiction flagrante avec le principe d’additivité des vitesses de la cinématique galiléenne,
en particulier parce que l’on peut l’écrire de façon symbolique « c+v=v » quelle que soit la
vitesse v de l’observateur, c étant la vitesse de la lumière.
Ces postulats, dont la formulation est extrêmement simples ont des conséquences
importantes pour la représentation du temps.
Une petite expérience permet de prendre l’ampleur des conséquences du second postulat.
Considérons une horloge battant « la mesure » en faisant osciller des photons entre deux
miroirs espacés d’une distance d (voir Fig. 2). Un observateur 1 au repos par rapport aux
miroirs observent que le faisceau lumineux est perpendiculaire aux miroirs si bien que le
temps aller-retour de la lumière (c.-à-d. la période de l’horloge) est T = 2d/c où c est la vitesse
de la lumière dans le vide.
Supposons maintenant que l’horloge se déplace à une vitesse V par rapport au sol. Un
observateur 2 immobile par rapport au sol observera que la lumière a un trajet oblique. La
lumière se propageant toujours à la même vitesse (d’après le second postulat) et le trajet à
parcourir plus long, nous en déduisons que l’observateur 2 voit l’horloge battre plus
lentement. La longueur du trajet de la lumière pour l’observateur 2 est D=2√(d2+(V T’/2)2),
T’ étant la période de l’horloge mesurée par l’observateur 2. Comme D=cT’, on en déduit que
T’=T/√(1-v2/c2).
Le second postulat implique donc que la période d’une horloge dépend de son état de
mouvement : un observateur au repos par rapport à l’horloge la voit battre plus rapidement
qu’un observateur en mouvement par rapport à elle. Il s’agit là d’un phénomène relativiste,
appelé dilatation du temps, et absent de la description classique de l’espace et du temps. La
période mesurée par l’observateur au repos par rapport à l’horloge sera appelée période
propre. Tout observateur aura ainsi un temps propre qui est celui qu’il mesure avec une
horloge qui se déplace avec lui. On peut synchroniser des horloges qui sont au repos les unes
par rapport aux autres mais nous ne pouvons plus parler de temps absolu.