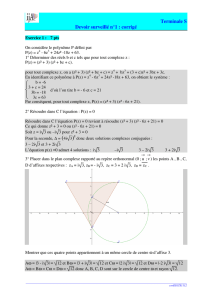
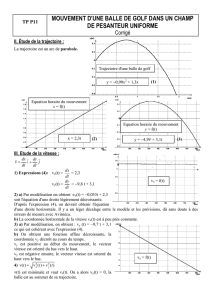
Le disque remontant un plan incliné 2.Étude théorique de la

I.N.R.P. – B. Richoux, C. Salvetat, Lycée J.-B. Corot, Savigny s/orge 18/10/02 1/1
Le disque remontant un plan incliné
2.Étude théorique de la première phase
2.1.Théorèmes généraux
L’application de la relation fondamentale au disque
permet d’écrire, dans un référentiel terrestre considéré
galiléen :
 avec le théorème de la résultante cinétique,
 avec le théorème du moment cinétique en G
2.2.Projection sur les axes (O,x,y)
Le mouvement de G est un mouvement rectiligne
selon Oy.
Le mouvement relatif est un mouvement de rotation
autour d'un axe passant par G et donc :
Ces équations deviennent avec J = ½ mR² :
Si N est toujours positif, il reste à discuter le signe de
T.
2.3.Équation différentielle
La définition de la vitesse de glissement permet
d'écrire, sachant que le plan est fixe :
Au départ la vitesse de glissement n'est pas nulle (car
v0 est imposée) et donc il existe obligatoirement un
glissement et la réaction tangentielle est un vecteur
opposé à la vitesse de glissement donc T < 0 :
 On déduit de (1) que l'accélération sur Ox est
constante :
 On déduit de (3) que l'accélération angulaire
est constante :
En intégrant ces deux équations on constate que :
 l'accélération constante mais négative implique
un mouvement de translation uniformément
retardée, puisque la vitesse est toujours
positive dans cette phase,
 l'accélération angulaire constante mais
négative implique un mouvement de rotation
autour de G uniformément accéléré puisque la
vitesse angulaire est toujours négative dans
cette phase.
am=++ PNT
iTjR ∧−=∧= TGI
dt
dG
σ
Tmgxm +−=αsin
&&
0cos =+−= Nmgym α
&&
kRTkJ =ϕ
&&
m
T
gx +−=αsin
&& (1)
αcosmgN = (2)
mR
T
2
=ϕ
&& (3)
ℜ∈ℜ∈ −= // planIdisqueIg vvv
ℜ∈
=/disqueIg vv
GIk
dt
d
vv Gg ∧+= ℜ
ϕ
/
iRixvgϕ
&& +=
α
cosfmgNfT −=−=
Æαα cossin fggx −−=
&&
Æ
R
fg α
ϕcos2−
=
&&
Æ0
)cos(sin vtfgx +−−=αα
&
Æt
R
fg α
ϕcos2 −=
&