Calcul de champ électrique : exemple simple

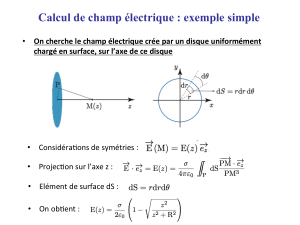
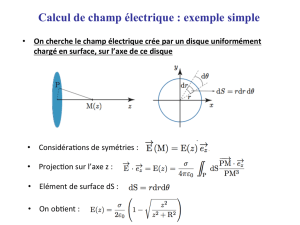
Calcul de champ électrique : exemple simple
• !"#$%&'$%&#(&#$%)*+#,(&$-'./0&#$',&#+)'#0"#1.2/0&#0".34'*,*&"-#
$%)'5,#&"#20'3)$&6#20'#(7)8&#1&#$&#1.2/0&!
• "#$%&'()*+#$%!',!%-.(/)&,%!0!!
• 1)#2,3+#$!%4)!56*7,!8!0!!
• 9$!#:+,$/!0!!
• ;5(.,$/!',!%4)<*3,!'=!0!!

Calcul de champ électrique : le théorème de Gauss
• >*$%!',%!3*%!?(#.(/)&@4,.,$/!A!%&.B5,%!C!DB)(%,$/*$/!',%!%-..(/)&,%!
,/!&$E*)&*$3,%FG!&5!,%/!%#4E,$/!B54%!%&.B5,!'64+5&%,)!5,!/H(#)I.,!',!J*4%%!
@4,!',!3*5345,)!',%!&$/(?)*5,%!.45+B5,%K!
#
• 9&#-%,4':*&#27&8+'.*&#;#
<&#=(08#10#$%)*+#,(&$-'./0&#>#-')?&'2#-40-&#20'3)$&#3&'*,&#&2-#,5)(#>#()#
$%)'5&#$4"-&"0&#1)"2#(&#?4(0*&#1,(.*.-,#+)'#()#20'3)$&#3&'*,&6#1.?.2,&#+)'#
()#+&'*.@?.-,#10#?.1&A!

Notion de flux et d’angle solide
9$!&$/)#'4&/!(7)"5(&#24(.1&#;!
B'4+'.,-,2#;!56!*$?5,!%#5&',!'64$,!%4)<*3,!
<,).(,!E4,!',B4&%!56&$/()&,4)!',!3,55,L3&!
E*4/!MNK!O4,!',B4&%!56,7/()&,4)!',!3,55,L3&!
E*4/!8()#K!

Démonstration du théorème de Gauss
P,!Q47!'4!3H*.B!3)(,!B*)!4$,!3H*)?,!@!R!/)*E,)%!4$,!%4)<*3,!E4,!%#4%!4$!*$?5,!
%#5&',!S!E*4/!
P,!Q47!R!/)*E,)%!4$,!%4)<*3,!'64$!,$%,.:5,!',!3H*)?,%!@&!E*4/!'#$3!!
=&!56#$!3#$%&'I),!4$,!%4)<*3,!<,).(,G!S&!E*4/!8()#!%&!5*!3H*)?,!@&!,%/!,7/()&,4),!
*4!E#54.,!'(5&.&/(!B*)!5*!%4)<*3,G!,/!MN!%&!,55,!,%/!R!56&$/()&,4),K!9$!#:+,$/!
'#$3!5,!)(%45/*/!%#4H*&/(!