6 angles cours II 5

ANGLES
1) Définition.
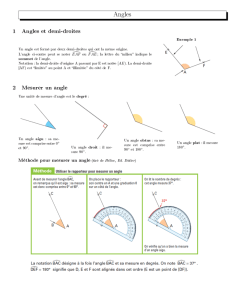
Définition :L’angle
AOB
ou
BOA
est la portion du plan délimité par les
deux demi-droites [OA) et [Ob) de même origine O.
Le point O est le sommet de l’angle (lettre O toujours placé au
milieu dans
AOB
). Les demi-droites [OA) et [OB) sont les cotés de
l’angle.
Remarque deux droites sécantes
définissent QUATRE angles.
AON
,
BOM
sont supperposables , on
les code avec la m^eme marque. Idem pour
NOB
et
M O A
Remarque 1 : les angles NÔM et AÔN ont même mesure , on peut les
superposer , on les code avec la même marque.
Remarque 2 : Une figure complexe
peut définir un grand nombre
d’angles (ici 21 angles !).
Remarque 3 : Un sommet seul ne
suffit pas à déterminer un angle :
ACB
,
ACJ
et
JCB
sont bien des angles différents de même sommet C.
Pour s’entraîner : ex 5 , ex. 11
angles ADJACENTS
Définition : Les angles
AJC
et
JCB
sont dit ADJACENTS quand ils ont
le sommet en commun et quand ils sont situés de part et d’autre d’un coté
commun.
Marque de l’angle pour le coder
Sommet de l’angle
[OA) et [OB)
: côtés
de l’angle
O
A
B

Non Adjacents
Pas de sommet
commun
Non Adjacents
Pas de côté
commun
Adjacents Non Adjacents
Ils ne sont pas DE PART ET
D’AUTRE du côté commun
Reporter un angle avec un compas
Reporter l’angle SRT , a partir de
l’origine P
On trace un cercle de centre R, il coupe
les côté [RS) et [RT) en A et B.
En gardant le même écartement on
trace un cercle de centre P , On
place un point A’ sur celui-ci
On reporte la longueur AB , a l’aide d’un compas, a
partir de A’ telle que A’B’=AB et B’ est sur le cercle
de centre P
On obtient un Angle A’PB’ de même mesure que
SRT
Pour s’entraîner : ex 4B , ex. 15
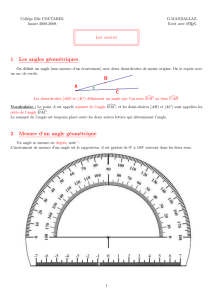
2) Mesure d’un angle
Comme une règle graduée mesure un segment le rapporteur permet de
mesurer un angle : exemple xOy= 44° et
uOv
=50°
Tracer un angle aigu
BOA
=74° dans les quatre situations
u
v

L’unité de mesure d’un angle est le degrés noté °
(Sur les calculatrices on voit DEG ou D)
Exemple
ABC
=45° , à ne pas confondre avec l’unité detempérature le
degrés Celsius noté : °C .
On rencontre aussi des angles en Radian , rad, (calculatrice : RAD ou R) :
π est un angle en Radians !.
ABC
= π rad ≈ 3,14159 rad = 180°
xOy=57,1
2
≈
π
radians = 90° (angle droit)
autres unités (non utilisée en sixième ) : Le grade Gr (sur les claculatrices :
GRA ou G) , 200 GRA=180° , 90°=100Gr, il apparaît parfois sur les
rapporteurs ! ne pas l’utiliser.
….et aussi en millièmes (mils) utilisé dans l’armée…
Pour s’entraîner : ex 3 , ex. 4 , ex. 12, ex. 13, ex. 14 , ex. 14B, ex. 16

3) Classification des angles en fonction de leur mesure .
ANGLES AIGUS ANGLES OBTUS
Mesure entre 0° et 90° inclus Mesure entre 90° et 180° inclus
AOB est un angle aigu AOB est un
angle
obtus
Angle nul
Mesure : 0°
Angle droit
Mesure : 90°
Angles plat
Mesure : 180°
Pour s’entraîner : ex. 6
4 Bissectrice d’un angle
définition : La bissectrice d’un angle est la demi-droite , d’origine le
sommet de l(angle , qui partage l’angle en deux angles adjacents de même
mesure .
Pour la tracer on peut utiliser le rapporteur en divisant la mesure de l’angle
AOB
par deux.
O
A
B
C
[OC) est la bissectrice de l’angle
AOB
A O B
= 30°

Autre Méthode de construction d’une bissectrice avec le compas
la demi-droite [AP) est la bissectrice de l’angle
BAC
.
AMPN est un losange, les diagonales d’un losange sont les bissectrices
des angles au sommet .
Pour s’entraîner : ex 2 , ex. 1 , ex. 7, ex. 14C