Rochambeau 2015. Enseignement spécifique

Rochambeau 2015. Enseignement spécifique
EXERCICE 2 (5 points) (candidats n’ayant pas suivi l’enseignement de spécialité)
On se place dans un repère orthonormé et, pour tout entier naturel n,ondéfinitlespoints(An)par leurs coordonnées
(xn,y
n)de la façon suivante :
!x0=−3
y0=4 et pour tout entier naturel n:!xn+1 =0,8xn−0,6yn
yn+1 =0,6xn+0,8yn
1) a) Déterminer les coordonnées des points A0,A1et A2.
b) Pour construire les points Anainsi obtenus, on écrit l’algorithme suivant :
Variables :
i, x, y, t :nombresréels
Initialisation :
xprend la valeur −3
yprend la valeur 4
Traitement :
Pour iallant de 0 à 20
Construire le point de coordonnées (x, y)
tprend la valeur x
xprend la valeur . . . .
yprend la valeur . . . .
Fin Pour
Recopier et compléter cet algorithme pour qu’il construise les points A0àA20.
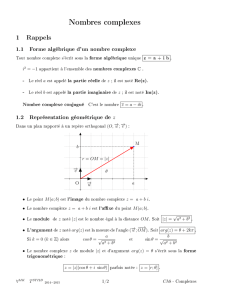
c) Al’aided’untableur,onaobtenulenuagedepointssuivant:
1
2
3
4
5
−1
−2
−3
−4
−5
−6
1234567−1−2−3−4−5−6−7
Identifier les points A0,A1et A2.Onlesnommerasurlafigurejointeenannexe 2, (à rendre avec la copie).
Quel semble être l’ensemble auquel appartiennent les pointsAnpour tout nentier naturel ?
2) Le but de cette question est de construire géométriquement les points Anpour tout nentier naturel.
Dans le plan complexe, on nomme, pour tout entier naturel n,zn=xn+iynl’affixe du point An.
a) Soit un=|zn|.Montrerque,pourtoutentiernatureln,un=5.
Quelle interprétation géométrique peut-on faire de ce résultat ?
b) On admet qu’il existe un réel θtel que cos(θ)=0,8et sin(θ)=0,6.
http ://www.maths-france.fr 1 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.

Montrer que, pour tout entier naturel n,eiθzn=zn+1.
c) Démontrer que, pour tout entier naturel n,zn=einθz0.
d) Montrer que θ+π
2est un argument du nombre complexe z0.
e) Pour tout entier naturel n,déterminer,enfonctiondenet θ,unargumentdunombrecomplexezn.
Représenter θsur la figure jointe en annexe 2, (à rendre avec la copie).
Expliquer, pour tout entier naturel n,commentconstruirelepointAn+1 àpartirdupointAn.
http ://www.maths-france.fr 2 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.

Annexe 2
1
2
3
4
5
−1
−2
−3
−4
−5
−6
1234567−1−2−3−4−5−6−7
http ://www.maths-france.fr 3 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.

Rochambeau 2015. Enseignement spécifique
EXERCICE 2 : corrigé
1) a)
•x0=−3et y0=4.Donc,A0(−3; 4).
•x1=0,8x0−0,6y0=0,8(−3)−0,6(4) = −4,8et y1=0,6x0+0,8y0=0,6(−3)+0,8(4) = 1,4.DoncA1(−4,8; 1,4).
•x2=0,8x1−0,6y1=0,8(−4,8) −0,6(1,4) = −4,68 et y2=0,6x1+0,8y1=0,6(−4,8) + 0,8(1,4) =.Donc
A2(−4,68; −1,76).
b) Algorithme complété.
Variables :
i, x, y, t :nombresréels
Initialisation :
xprend la valeur −3
yprend la valeur 4
Traitement :
Pour iallant de 0 à 20
Construire le point de coordonnées (x, y)
tprend la valeur x
xprend la valeur 0,8×t−0,6×y.
yprend la valeur 0,6×t+0,8×y.
Fin Pour
Remarque. L’algorithme calcule les coordonnées des points A0, ..., A21.
c) Graphique.
1
2
3
4
5
−1
−2
−3
−4
−5
−6
1234567−1−2−3−4−5−6−7
A0
A1
A2
Il semble que tous les points Ansoient sur le cercle de centre Oet de rayon 5.
2) a) Montrons par récurrence que pour tout entier naturel n,|zn|=5.
•z0=−3+4iet donc |z0|=!(−3)2+4
2=√9+16=√25 = 5.L’égalitéàdémontrerestdoncvraiequandn=0.
•Soit n!0.Supposonsque∥zn|=5.
http ://www.maths-france.fr 1 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.

|zn+1|="x2
n+1 +y2 n+1 ="(0,8xn−0,6yn)2+(0,6xn+0,8yn)2
=!0,64x2
n−2×0,8×0,6xn+0,36y2 n+0,36x2 n+2×0,8×0,6xn+0,64y2 n
=!x2
n+y2 n=|zn|
=5(par hypothèse de récurrence.)
On a montré par récurrence que pour tout entier naturel n,|zn|=5et donc que tous les points Ansoient sur le cercle
de centre Oet de rayon 5.
b) Soit nun entier naturel.
eiθzn=(cosθ+isin θ)(xn+iyn)=(0,8+0,6i)(xn+iyn)
=0,8xn+0,8iyn+0,6ixn−0,6yn=(0,8xn−0,6yn)+i(0,6xn+0,8yn)
=xn+1 +iyn+1 =zn+1.
c) La suite (zn)n∈Nest donc une suite géométrique de raison q=eiθ.Onsaitquepourtoutentiernatureln,
zn=z0×qn=z0#eiθ$n=z0einθ.
d) Soit αun argument du nombre complexe z0=−3+4i.Ona|z0|=5puis
z0=5%−3
5+4 5i&=5(−0,6+0,8i)=5(−sin(θ)+icos(θ)) = 5 'cos 'θ+π 2(+isin 'θ+π 2((.
Ceci montre qu’un argument de z0est θ+π
2.
e) D’après les questions c) et d), pour tout entier naturel n,
zn=z0einθ=5ei(θ+π
2)einθ=5ei(nθ+θ+π 2)=5ei((n+1)θ+π 2).
Pour tout entier naturel n,unargumentdeznest (n+1)θ+π
2(et le module de znest 5).
5cos(θ)=5×0,8=4et 5 sin θ=5×0,6=3.Donc,θest un argument de 4+3i.
1
2
3
4
5
−1
−2
−3
−4
−5
−6
1234567−1−2−3−4−5−6−7
A0
A1
A2
θ
Pour tout entier naturel n,An+1 est obtenu en faisant tourner Anautour de Od’un angle de mesure θdans le sens
direct.
http ://www.maths-france.fr 2 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.