4 cosinus cours II 2

A
B
C
0) Rappels : Triangle rectangle.
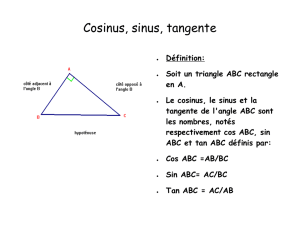
On dit qu’un triangle est rectangle quand l’un de ses 3 angles est droit.
Exemple :
ABC est un triangle rectangle en A.
BACest l’angle droit.
ABC
et
ACB
^ sont les deux angles aigus complémentaires (leur somme fit 90°).
Les Côtés [AB] et [BC] sont adjacents à l’angle ABC.
Le côté opposé à l’angle droit est toujours l’hypoténuse ( toujours plus grand que les deux autres côtés)
Exercice calculer la mesure de l’angle ABC sachant que ACB=70°
Pour s’entraîner : ex. 1
1) Cosinus d’un angle aigu.
Dans un triangle rectangle, le rapport du côté adjacent et de l’hypoténuse ne dépend que de l’angle aigu
qu’ils forment. On appelle ce rapport le cosinus de l’angle aigu.
ALORS cos
ABC
^ = ''
"
"BC BA
BC
BA
BC
BA ==
On écrit souvent :
cos
ABC
^ = hypoténuse Bàadjacentcôté ^CA
Moyen mnémotechnique : COS= Hypoténuse
adjacentCôté
⋅
Remarques :Dans le triangle ABC rectangle en A il y a deux angles aigus :
ABC
et
ACB

cos
ABC
^ = BC
BA cos
ACB
^ =
BC
AB
Remarques :
• Cette formule n’est valable que dans un triangle rectangle !
• Le cosinus de n’importe quel angle aigu est TOUJOURS compris entre 0 et 1
• Le cosinus d’un angle d’unité ! cos(
ABC
)= 923.0
13
12 ≈
cm
cm
• Conseil : calculer toujours un cosinus au moins au milième.
2) Utilisation de la calculatrice
Vous devez savoir changer les modes degres (DEG, D), radian (RAD, R),
grade (GRA, G) Sachant qu’au collège on veut toujours travailler en DEGRE
Savoir changer le « mode des angles » :
Fx 82 , Fx 92 : mode mode
Deg Rad Gra
1 2 3
Fx 92 collège 2D SHIFT SET UP 3 Deg 4 Rad 5 Gra
collège 2D+ SECONDE CONFIG 3 Deg 4 Rad 5 Gra
TI 30XIIB DGR DEG RAD GRA
TI 40 collègeII DR DEG RAD
TI / TI collège MODE ►… ► DGR DEG RAD GRA
LEXIBOOK DRG
exemple : déterminer cos(36°).
On utilise la fonctionnalité cos ou TRIG COS
Tape sur les touches 3 6 cos (ou sur cos 3 6 = ; ça dépend de ta calculatrice).
Tu peux alors lire le résultat : 0.8090169 .
La réponse est donc : cos(36°) ≈ 0,81 à 0,01 près,
ou : cos(36°) ≈ 0,809 à 0,001 près, . . .
Prendre au millième par défaut.
Hypoténuse [CB]
[AB] est le côté adjacent à
ABC
[AB] est le côté opposé à
ACB
[AC] est le côté adjacent à
ACB
[AC] est le côté opposé à
ABC
A
B
C

déterminer une valeur de
DEF
sachant que cos (
DEF
) = 0,2.
On utilise la fonction cos-1 , Acos , Acs , Arccos de la calculatrice
Qui s’obtient avec la séquence
2nd cos , inv cos , TRIG cos-1 , SHIFT cos
le résultat de la calculatrice : 78.46304097 .
La réponse est donc :
DEF
≈ 78° à 1° près,
ou :
DEF
≈ 78,5° à 0,1° près, ou :
DEF
≈ 78,46° à 0,01° près, . . .
( ne pas copier Tape sur les touches 0 , 2 inv cos ou 0 , 2 2nd cos
ou 2nd cos 0 , 2 =
ou cos-1 0 , 2 =
ou 2nd TRIG => => cos-1 0 , 2 =
ou seconde cos 0 , 2 =
ou SHIFT cos 0 , 2 = . ne pas copier )
le résultat de la calculatrice : 78.46304097 .
La réponse est donc :
DEF
≈ 78° à 1° près,
ou :
DEF
≈ 78,5° à 0,1° près,
ou :
DEF
≈ 78,46° à 0,01° près, . . .
Attention : Piège !: calculer
ABC
sachant que cos (
ABC
) = 72,0 ,
il faut taper sur les touches
2nd cos ( 0.2
÷
7 ) = . 88.36
et non 2nd cos 0.2
÷
7 = . 11.20
Pour s’entraîner : ex. 2
3 Exemple d’application :
Application 1 calcul d’un angle aigu lorsque l’on connaît l’hypoténuse et le côté adjacent.
Exemple : ABC est un triangle rectangle en A tel que AB = 4 cm et
BC = 8 cm. Calculer la mesure de
ABC
.
Rédaction : METHODE :
Faire ou compléter un dessin avec les données de l’énoncé
1 ABC est un triangle
rectangle en A donc 1. On écrit la formule du cosinus avec les bonnes hypothèsese.
4cm
8cm

cos
ABC
= BA
BC
2. cos
ABC
= 4
8 2. On remplace les noms des côtés connus par leur valeur.
3. cos
ABC
= 0,5 3. On effectue les calculs.
4.
ABC
= 60°
4. Avec l’aide de la touche cos-1 ou Asc de la machine (en
mode « degrés »), on retrouve la mesure de l’angle en degré.
( aux unités ! précision).
Pour s’entraîner : ex. 3 , ex. 4 , ex. 5
Application 2 Calcul d’un côté adjacent , connaissant l’hypoténuse et
un angle aigu.
Exemple : ABC est un triangle rectangle en A tel que BC = 9 cm et
ABC
= 30°. Calculer la longueur de [BA] au milimétre prés.
Rédaction METHODE :
Faire ou compléter un dessin avec les donnée de l’énoncé
Dans le triangle rectangle en ,
A, ABC on a
cos
ABC
= BA
BC
1. On écrit la formule du cosinus avec les bonnes hypothèsese.
cos 30 = BA
9 2. On remplace les côtés et angles connus par leur valeur.
0,866 ≈ BA
9 3. On effectue les calculs à l’aide de la touche cos de la machine (
en mode « degrés » et au millième pour le cosinus!).
BA ≈ 0,866 × 9 ≈ 7,7942 4. On isole le côté inconnu en « le multipliant de l’autre côté du = ».
AB≈7,8 cm 5. On conclu ( attention aux unités précision)
Remarque BA ≈ 0,8 × 9 ≈ 7.2 ,
Pour s’entraîner : ex. 6 , ex. 7 , ex. 8
Application 3 Calcul de la longueur de l’hypoténuse , connaissant un angle et son
coté adjacent.
Exemple :ABC est un triangle rectangle en A tel que AB = 7 cm et
ABC
= 40°. Calculer la
longueur de [BC]. Au millimetre près
METHODE :
Faire ou compléter un dessin avec les
données de l’énoncé
Dans le triangle rectangle en , A, ABC on a
cos
ABC
= BA
BC
1. On écrit la formule du cosinus avec les
bonnes hypothèsese

cos 40 = 7
BC ,
cos40×BC=7
BC= 40cos
7
2. On remplace les noms des côtés et
angles connus par leur valeur.
on isole BC : produit en croix , puis isoler
BC
BC≈766.0 7≈9,1378
3. On effectue les calculs à l’aide de la
fonction cos de la machine ( mode
« degrés » et au millième !) .
BC ≈ 7
0,766 ≈ 9,1 BC ≈ 9,1 cm 4. on conclu ( à la précision aux
unités)
Remarque si je prend cos40°≈0.7 (0.1 prés) je trouve BC≈10
7.0
7≈
cos40°≈0.76 (0.01 prés) BC≈2.9
76.0
7≈
cos40°≈0.766 (0.001 prés) BC≈1.9
766.0
7≈
cos40°≈0.7660 (0.001 prés) BC≈1.9
7660.0
7≈
conclusion On prend généralement toujours au millième ou au dix millième pour la VA d’un cosinus.
Pour s’entraîner : ex. 9 , ex. 10
4) quart de cercle trigonométrique
c est un quart de cercle de rayon 1 cm.
De centre O et O I J est un repère orthogonal
M
∈
c. [MH]┴[OI]
Cos
MOI
= OH
Démonstration
cos
MOI
=OM
OH or OM=1 donc Cos
MOI
= OH
Pour s’entraîner : ex. 9 , ex. 10
5 ) Résoudre des exercices sur les angles et cosinus de niveau Brevet : ex. 11 , ex. 12 , ex. 13 , ex. 14, ex. 15