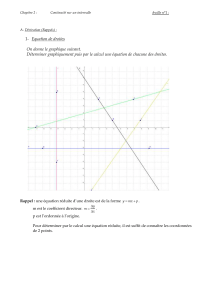
Poisson-Laplace et Chaleur - moodle@insa

Equations aux Dérivées Partielles (EDP):
équations de Poisson-Laplace et équation de la chaleur
1. Introduction et plan
De nombreux phénomènes physiques (au sens large) peuvent être représentés, modélisés, par une Equation
aux Dérivées Partielles (EDP). Une EDP est une équation reliant une fonction de plusieurs variables et ses
dérivées partielles.
La résolution d’une EDP est à priori plus difficille que celle d’une Equation Différentielle Ordinaire (EDO)
du fait qu’une EDO relie une fonction et sa - ses dérivées qui ne portent que sur une seule variable.
L’ordre d’une EDP est défini, comme dans le cas des EDO: c’est l’ordre maximal des dérivées partielles
figurant dans l’équation.
Une EDP est linéaire s’il s’agit d’une combinaison linéaire de la fonction et de ses dérivées partielles.
Typiquement, une EDP linéaire d’ordre 2 s’écrit comme suit:
n
ÿ
i,j=1
aij
ˆ2u
ˆxiˆxj
(x1,..,x
n)+
n
ÿ
i=1
bi
ˆu
ˆxi
(x1,..,x
n)+cu(x1,..,x n)=f(x1,..,x n)
Où la variable d’espace est x=(x1...xn),nest la dimension de l’espace; l’inconnue est la fonction u(x).
Les coefficients {aij }i,j ,{bi}iet csont donnés ainsi que le second membre f(x).fest également appelé
terme source; cette fonction représente les forces ou apports extérieurs.
Le plan de cette session est le suivant:
•Premières EDP classiques.
•Equation elliptique linéaire type: l’équation de Poisson - Laplace.
•Equation parabolique linéaire type: l’équation de la chaleur.
Il existe de très nombreux ouvrages sur les EDP et leurs résolutions numériques. Nous renvoyons le lecteur tout
particulièrement vers celle-ci:
B. Mohammadi, J.-H. Saïac, “Pratique de la simulation numérique”. Dunod (Industries et Technologies),
2003.
2. Premières EDP classiques
Parmi les EDP que l’on retrouve dans de nombreux domaines de l’ingénierie, commençons par mentionner
les suivantes.
2.1. Les équations de Poisson et de Laplace. L’équation de Poisson s’écrit en dimension 1,≠u”(x)=
f(x), et en dimension ncomme suit:
≠u(x)=f(x)
Rappelons que: u=(
ˆ2u
ˆx2
1
+... +ˆ2u
ˆx2
n)=div(Òu).
Le terme source fest donné.
L´ ’équation de Poisson est une équation linéaire d’ordre 2.
Elle est linéaire en son inconnue u(x)tout simplement parce que l’opérateur Laplacien est un opérateur
différentiel linéaire.
Cette équation modélise les phénomènes de diffusion stationnaires (stationnaire signifie que les inconnues ne
dépendent pas du temps, elles ne dépendent que de la variable d’espace x); ou encore de nombreux systèmes à
l’état d’équilibre.
Lorsque f=0, on parle de l’équation de Laplace, et ses solutions usont appelées fonctions harmoniques.
2.2. Classification des EDP. Les EDP sont classées selon trois types : elliptiques, paraboliques ou hyper-
boliques, selon la même classification que les coniques. Cette classification basée sur un critère purement math-
ématique (non détaillé ici), correspond à des comportements qualitatifs de solutions radicalement différents.
1

Figure 2.1. Solution de l’équation de Poisson en mécanique des structures: membrane élas-
tique chargée avec la force f(x)=1’x; la membrane est fixée sur ses bords (u=0aux
bords).
L’équation de Poisson ≠u=fest l’équation elliptique linéaire d’ordre 2 type.
2.3. Conditions aux Limites. Un modèle mathématique basé sur une EDP doit être fermé en imposant des
conditions aux bords du domaine,également appelées conditions aux limites.
Autrement dit, une EDP d’inconnue uposée dans un domaine ,xla variable d’espace, xœ, doit être
accompagnée de conditions sur usur le bord du domaine (ou potentiellement à l’infini si est non borné).
La nature et le nombre de ces conditions aux limites dépendent du problème physique posé mais aussi du
type de l’EDP i.e. elliptique, parabolique ou hyperbolique.
Pour chaque équation étudiée, le type de CL envisageable sera précisé.
Figure 2.2. A 2d domain and its boundary ˆ.is an open set, bounded.
2.4. L’équation de la chaleur. L’équation de la chaleur s’écrit en dimension 1,ˆu
ˆt(x, t)≠⁄ˆ2u ˆx2(x, t)=
f(x, t), et en dimension ncomme suit:
ˆu
ˆt(x, t)≠div(⁄Òu)(x, t)=f(x, t)
L’inconnue u(x, t)dépend de la variable d’espace xet de la variable temporelle t.
L’équation de la chaleur est linéaire d’ordre 2 en espace et d’ordre 1 en temps. C’est l’équation parabolique
linéaire d’ordre 2 type.
Ce modèle doit étré fermé avec des conditions aux bords, du même type que celles de l’équation de Poisson-
Laplace, mais aussi d’une condition initiale u|t=0 =u0donné.
Notons que dans le cas stationnaire (une dépend plus du temps t), cette équation se simplifie en équation
de Poisson.
L’équation de la chaleur, introduite par J.-B. Fourier au début du XIXème siècle, modélise des phénomènes
de diffusion-dissipation; typiquement la diffusion thermique au sein du milieu (⁄est alors de coefficient de
diffusivité thermique), mais aussi la diffusion de particules atomiques (phonons, électrons), certains aspects
probabilistes du mouvement brownien, ou encore en mathématiques financières la dynamique prix d’une action
(équation de Black-Scholes).
2.5. Autres EDP classiques.
Parmi les EDP classiques, mentionnons également l’équation biharmonique qui s’écrit:
≠2u(x)=f(x)
2

Figure 2.3. Solution de l’équation de la chaleur 2d sans terme source (f=0).
(G) La CI u(x, 0) = u0(x)donnée (M) La solution à un temps t1>0:u(x, t1)(D) La solution
àuntempst2>t
1:u(x, t2). La température udiffuse au cours du temps. Image Wikipédia.
où: 2u(x)=qn
i=1
ˆ4u
ˆx4
i
(x)+2qn
i,j=1;i<j
ˆ4u
ˆx2
iˆx2 j
(x).
C’est une équation linéaire d’ordre 4 qui modélise par exemple la forme d’équilibre d’une
plaque en flexion; u(x)représente alors le déplacement de la plaque au point x, voir la figure
ci-dessous.
Cette équation est de type elliptique.
Figure 2.4. Solution de l’équation biharmonique: déplacement d’une plaque compressée sur
deux de ses bords (uimposé sur ces bords-ci) et libre sur les deux autres bords.
Nous étudierons durant une prochaine session bien d’autres EDP linéaires classiques, notamment l’équation
de transport:
ˆu
ˆt(x, t)+˛v·Òu(x, t)=0
où ˛vest un champ de vitesse donné qui transporte la quantité scalaire u(x, t)dans le milieu considéré.
Exemple en mécanique des fluides: ureprésente la concentration d’une substance chimique dans un écoule-
ment de fluide (ex 1d, une rivière). Il s’agit d’une équation linéaire d’ordre 1.
Figure 2.5. Equation de transport 1d: solution ureprésentée dans le repère (x, t)
Nous verrons également l’équation des ondes:
ˆ2u
ˆt2(x, t)≠c2u(x, t)=0
où cest la vitesse de propagation de l’onde udans le milieu considéré.
En acoustique, ureprésente par exemple l’amplitude d’une onde sonore qui se propage dans l’air.
Il s’agit d’une équation linéaire d’ordre 2 en espace et en temps.
Ces deux dernières équations (transport et ondes) représentent les deux équations hyperboliques types.
3

Figure 2.6. (G) Deux ondes planes se croisent, se superposent et poursuivent leur propagation.
L’une est progressive, l’autre est régressive (terminologie liée au sens de la propagation).
(D) Propagation d’une onde dans le plan (x, t)(l’une est progressive, l’autre est régressive).
On y observe la C.I. u(x, 0) (=le pic unique) et ˆxu(x, 0) = 0 (vitesse initiale nulle). Image:
3. Equation elliptique linéaire: l’équation de Poisson-Laplace
L’équation elliptique linéaire type (et aussi la plus simple) est l’équation de Poisson ≠u(x)=f, ou encore
plus généralement l’équation suivante:
≠div(⁄Òu(x)) = f(x)dans 
est la géometrie du domaine, ⁄est donné, potentiellement dépendant de x. Rappelons que:
div(Òu)=u.
3.1. Exemples d’application.
Cette équation d’équilibre est omniprésente en modélisation, citons les exemples suivants.
(1) En thermique, cette équation modélise la diffusion du champ de température u(x)au sein d’un milieu
ou matériau de géométrie .
Le coefficient ⁄est alors la diffusivité thermique du matériau et fun éventuel terme source extérieur.
Le modèle doit être fermé en imposant des conditions aux limites.
Pour cette équation, les conditions imposées sur le bord du domaine ˆ, devront être une des conditions
suivantes.
(a) La température est donnée: u=ud. Il s’agit des conditions de Dirichlet.
(b) Le flux de température est donné: ≠⁄Òu·n=Ï. Il s’agit des conditions de Neumann.
Le vecteur ndésignera toujours la normale sortante au bord.
Dans le cas d’une paroi isolée, on aura: Ï=0, conditions de Neumann homogène.
Cette condition de flux nul au bord peut également représenter une symétrie de la solution, ou
encore une condition de sortie libre dans le cas d’une frontière ouverte.
(c) Une combinaision linéaire des deux conditions précédentes: ≠⁄Òu·n=–u+Ï.
Il s’agit des conditions de Robin, aussi dites de Fourier.
Ces conditions de Fourier représentent, modélisent, un flux dépendant linéairement de la valeur de
u.
En thermique, cela traduit un échange convectif sur une paroi.
En propagation d’ondes, cela traduirait les effets d’un matériau absorbant.
(d) Les conditions aux limites sont dites mixtes lorsque l’on considère plusieurs types de C.L.; par
exemple une condition de Dirichlet est imposée sur det une condition de Neumann est imposée
sur n. Attention on ne peut imposer qu’une seule CL par morceau du bord, c’est à dire que dans
notre exemple on aurait nécessairement: dfin=ˆ.
Pour une équation elliptique une condition est requise sur l’intégralité du bord ˆ.
4

(2) En mécanique des structures, cette équation modélise le déplacement d’une membrane plane élas-
tique fixée sur son bord ˆ.ureprésente alors le déplacement de la membrane, déplacement perpen-
diculaire au plan défini par , voir la figure précédente Fig. 2.1.
(3) En électrostatique, ureprésente le potentiel électrique associé à la distribution de charges f, voir la
figure ci-dessous.
Sur ces deux exemples, vous noterez notamment l’aspect régulier de la solution.
Figure 3.1. Solution de l’équation de Poisson: potentiel électrique udans un anneau avec
u=0sur le bord intérieur et u=Rsin(5◊)sur le bord extérieur de rayon R. Source Wikipédia.
3.2. Propriétés fondamentales de la solution.
3.2.1. Principe du maximum. Considérons le problème dit de Dirichlet suivant:
u(x)=0dans avec u(x)=g(x)sur ˆ
Toute fonction solution u(x)est par définition une fonction harmonique (son laplacien est nul).
On peut alors montrer que uatteint ses extrema (minima et maxima) sur le bord de ˆ, et non à l’intérieur de
.
Cette propriété s’appelle le principe du maximum.
Notons bien que le terme source fest nul.
Par ailleurs, il est facile de démontrer que cette propriété du maximum implique l’unicité de la solution u.
3.2.2. Propriété de la moyenne. La propriété de la moyenne s’énonce ainsi: la valeur de u, fonction harmonique,
est en tout point égale à la moyenne de ses valeurs alentours.
Autrement formulé, on a:
u(x)= 1
|B1,n|rnˆBn(x,r)
u(x)dx
où |B1,n|est la mesure de la boule unité de Rn.
Dans les exemples donnés précédemment, cette propriété se traduirait ainsi:
la valeur à l’équilibre de la quantité modélisée (température, déplacement, potentiel´electrique) est égale à la
moyenne de ses valeurs environnantes.
(Rappelons que cela reste vrai en l’absence de terme source extérieur f).
Notons enfin que les schémas aux différences finies que nous allons construire par la suite vérifierons également
cette propríe´ te de la moyenne.
5