Théorie du producteur

Xavier Timbeau
[email protected]po.fr
ECO1 Introduction à l’économie
Amphi 3
Théorie(s) du producteur

Théorie(s) du producteur
La fonction de production
Cardinale, inputs, outputs
Rendements croissants, constants, décroissants
Coût fixe, coût variable
Taux marginal de substitution
Minimiser le coût: le choix du plan de production optimal
Programme du producteur
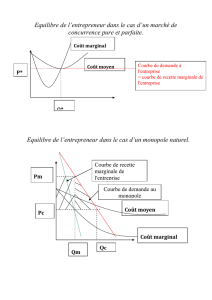
Représentation graphique
Cout marginal et coût moyen
Court terme et long terme, facteurs fixes
Maximiser le profit: fonction d’offre
Profit et programme du producteur
Concurrence parfaite, fonction d’offre, fonction d’offre agrégée
Monopole
Il n’y a pas de fonction d’offre!

La fonction de production
Représentation de la technologie de production
  où les sont les outputs, les sont les inputs
Un seul output : croissante en les inputs,   
  un seul output deux inputs
  fonction de production Cobb-Douglas
Notion de plan de production:
Un vecteur et on note les inputs négatifs et les outputs positifs (ou nuls)
Notation utile puisque les inputs sont produits par quelqu’un (chaîne de valeur)
Isoquantes de production et TMS
Production de croissante

Rendements
On appelle rendement
De combien est multipliée la production lorsqu’on double les inputs
Si 2 rendements constants, supérieur à 2 croissants, inférieur à 2 décroissants
Coût fixe et coût variable
Le coût fixe est la quantité d’inputs qu’il faut pour produire une quantité strictement positive
Pas nécessairement de chaque input
Coût variable (to be continued)
Dérivée de en fonction des différents inputs
Exemple: cas d’un seul input
    si   ;   si   
 est un coût perdu (sunk cost)
Si la fonction est concave, alors il
est possible d’avoir   pour 
assez grand

Optimiser la production: minimiser le coût
Minimiser le coût, indépendamment de la structure de marché
Un vecteur de prix d’input (donnés, pas de pouvoir de marché du producteur) 
Minimiser le coût, pour une production donnée (ou )
  sous contrainte    
Le programme dual : maximiser   sous contrainte de 
Le lagrangien s’écrit (un seul output)
Les conditions de premier ordre (CPO)