Angles inscrits, angles au centre

14
Angles inscrits,
angles au centre
CHAPITRE
est un quadrilatère inscrit dans un cercle
de centre .
Quelle est la mesure en degrés de l’angle ?
La figure est volontairement fausse.
Énigme du chapitre.
—Connaître etutiliser la relation entre un
angle inscrit et l’angle au centre qui in-
tercepte le même arc.
Objectifs du chapitre.

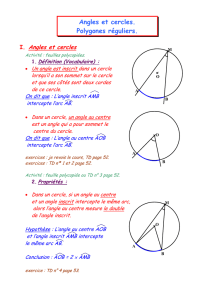
I/ Angles inscrits et angles au centre
Activité A. Angle inscrit et angle au centre
1. Reproduire une figure du même type que celle-ci pour laquelle le point est le centre du
cercle passant par les points , et .
2. Un angle inscrit dans un cercle est un angle dont le sommet est un point de ce cercle et
dont les côtés coupent ce cercle.
(a) Justifier que l’angle est un angle inscrit dans le cercle .
(b) Tracer en rouge l’arc de cercle le plus court reliant les points et . On dit que l’angle
inscrit intercepte l’arc de cercle .
3. Un angle au centre d’un cercle est un angle dont le sommet est le centre de ce cercle.
Par exemple, l’angle est un angle au centre du cercle . On dit qu’il intercepte
l’arc de cercle .
Citer deux autres angles au centre du cercle en précisant l’arc de cercle intercepté.

1) Angle inscrit dans un cercle
Définition
Un angle inscrit dans un cercle est un angle dont le sommet est un point de ce cercle et dont les
côtés coupent ce cercle.
Exemple
L’angle est un angle inscrit dans le
cercle ; il intercepte l’arc d.
2) Angle au centre dans un cercle
Définition
On appelle angle au centre d’un cercle un angle dont le sommet est le centre de ce cercle.
Exemple
Dans le cercle de centre , l’angle au
centre intercepte l’arc .
Faire les exercices 1 2 3

II/ De nouvelles propriétés
1) Avec un angle au centre et un angle inscrit
Activité B. Comparer un angle au centre et un angle inscrit
Partie A : Conjecture avec GeoGebra
1. (a) Placer un point sur la fenêtre Graphique.
(b) Créer un cercle de centre .
(c) Créer trois points , et sur ce cercle tels que l’angle soit aigu.
(d) Afficher l’angle inscrit qui intercepte l’angle et vérifier s’il est aigu.
(e) Créer les demi-droites et .
(f) Afficher la mesure de l’angle au centre qui intercepte le même arc .
(g) Que remarque-t-on ?
2. (a) Déplacer le point sur le cercle. Que constate-t-on ?
(b) Déplacer les points et sur le cercle. Que constate-t-on ?
Partie B : Démonstration
, et sont trois points du cercle de centre de telle sorte que les angles et
interceptent l’arc de cercle . On montre que .
1. Premier cas : est un diamètre du cercle. On désigne par la mesure en degrés de
l’angle .
(a) Quelle est la nature du triangle ? Justifier la réponse.
(b) Exprimer les mesures des angles du triangle en fonction de .
(c) En déduire la mesure de l’angle .

2. Deuxième cas : Le point appartient au
secteur angulaire . On appelle le
point du cercle de sorte que soit un
diamètre.
(a) Que dire des angles et ?
(b) Que dire des angles et ?
(c) Montrer alors que, dans ce cas, la pro-
priété est vérifiée.
3. Troisième cas : Le point n’appartient pas
au secteur angulaire .
En considérant le diamètre , montrer
comme au deuxième cas que
.
Propriété
Dans un cercle, si un angle inscrit et un angle au centre interceptent le même arc, alors l’angle
au centre mesure le double de l’angle inscrit.
Exemple
La figure ci-contre représente un cercle
de centre . L’angle dmesure ˚.
Dans le cercle, l’angle inscrit det l’angle
au centre interceptent le même arc .
Donc l’angle au centre mesure le
double de l’angle inscrit d.
d˚ ˚