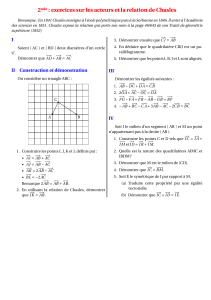
1 Transformations géométriques

A A
IdAA A x A x
f E
F g F E
g o f =IdEf o g =IdFf
f−1=g
P
−→
P
OΩ (∆) P
~u −→ P
T~u ~u
SO
(∆)
Ωk6= 0

A A
A f A A f o f =IdA
f f
f−1
P
C
f f(x) = x+ 2
x−1
I J
f−1
f−1
f
I
f I J =f < I >
f−1J
f I f0I
f−1J∀y∈J(f−1)0(y) = 1
f0(f−1(y))
f−1J f I
Cf−1Cf
D:y=x
f sinus I = [−π
2;π 2]
f I J
Arcsin f
f Arcsin
g cosinus K = [0; π]
g K L
Arccos g
g Arccos
h tangente M =] −π
2;π 2[

h M N
Arctan h
h Arctan
3
Arcsin Arccos Arctan
Arcsin(sin(x))
Arccos(cos(x))
Arctan(tan(x))
sin(Arcsin(x))
cos(Arccos(x))
tan(Arctan(x))
sin(Arccos(x))
cos(Arcsin(x))
∀y∈[−1; 1] Arcsin(y) + Arcos(y) = π
2
3Arcsin Arccos Arctan
(Arcsin)0(y) (Arccos)0(y) (Arctan)0(y)
y
c s R3
P1:∀x∈R(c(x))2−(s(x))2= 1
P2:∀x∈Rc(x) = s0(x)
P3:c(0) = 1
∀x∈Rc(x)6= 0
s(0)
P1∀x∈Rs(x) = c0(x)
u=c+s v =c−s
u(0) v(0)
u0=u v0=−v
u v
c(x)s(x)

2
f g Rf(x) = 1
2exg(x) = 1 2e−x
R1= (0,−→ u , −→ v) 2
2Cf
Cgf g 2
2 0 1
sh
sh Rsh(x) = ex−e−x
2
sh
sh sh
Csh sh
+∞Cf
Csh Cf
Csh sh
−∞ Ckk
Csh Ck
R1= (0,−→ u , −→ v)
Csh Ck0Csh
ch
ch Rch(x) = ex+e−x
2
ch
ch ch
Cch ch
+∞Cf
Cch Cf
Cch ch
−∞
Cch
−∞
R1= (0,−→ u , −→ v)
Cch 0Cch
+∞ch(x)∼1
2exsh(x)∼1 2ex
−∞ ch(x)∼1
2e−xsh(x)∼ −1 2e−x
a
ch2(a)−sh2(a) = 1

th
th Rth(x) = sh(x)
ch(x)
th
0
ch R+
R+J
argch
ch R+
R2
ch R+argch
1argch
y∈J argch(y) = ln(y+py2−1)
argch (argch)0(y)
sh R
K
argsh sh
R3
sh argsh
y∈K argsh(y) = ln(y+py2+ 1)
argsh (argsh)0(y)
th R
L
argth th
R4
th argth
y∈L argth(y) = 1
2ln(1 + y 1−y)
argth (argth)0(y)
a b
ch(a+b) = ch(a)ch(b) + sh(a)sh(b)
sh(a+b) = sh(a)ch(b) + sh(b)ch(a)
th(a+b) = th(a) + th(b)
1 + th(a)th(b)
ch(2a)sh(2a)
th(2a)
ch(x) = 1 + t2
1−t2sh(x) = 2t 1−t2th(x)2t 1 + t2
t=th(x
2)