PROBABILITÉS

1
PROBABILITÉS
en 3ème

2
Introduction
Pourquoi l’aléatoire au collège ?
Textes officiels
Expériences aléatoires
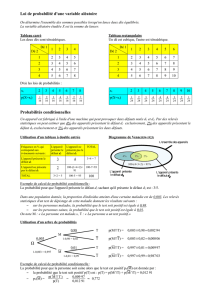
Notions élémentaires de probabilité
Un exemple d’activité
Conclusion

3
Introduction
Des représentations du hasard chez des élèves de CM2 :
– « Choses imprévisibles qui viennent de l’extérieur »
–« On produit du hasard en répondant au pif »
–« Choses relatives aux coïncidences »
–« Chose où on peut avoir de la chance ou de la malchance»
– « Le hasard n’existe pas »

4
Etymologie :
– Hasard vient de l’arabe « az-zahr » qui signifie jet de dé
–Aléa vient du latin alea qui signifie coup de dé
–Chance vient du latin cadere qui signifie choir, tomber

5
Pourquoi l’aléatoire au collège ?
« Pour permettre au citoyen d’aborder l’incertitude et le
hasard dans une perspective rationnelle »
Familiariser plus tôt les élèves avec cette branche des
mathématiques qui diffère fondamentalement des autres.
Une clé essentielle pour l’analyse et la compréhension des
phénomènes incertains.