Le diaporama de la leçon

ANGLES INSCRITS –POLYGONES REGULIERS
1. ANGLES INSCRITS –ANGLES AU CENTRE
a. Vocabulaire
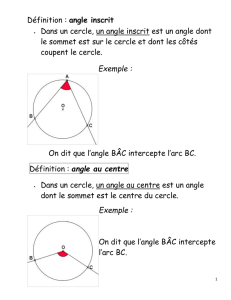
Soit (C) un cercle.A, Met B sont trois points distincts du cercle.
A
B
M
On dit que l’angle
BMA ˆ
est un angle inscrit
dans le cercle.
Les points de l’arc de
cercle AB appartiennent à
cet angle.
On dit que l’angle inscrit
BMA ˆ
intercepte l’arc AB.
Remarque : il y a une infinité d’angles
inscrits dans ce cercle qui interceptent
l’arc AB (ex : ).
BNA ˆ
N
Fabienne BUSSAC

Un angle au centre du cercle (C) est un angle dont le sommet est le
centre du cercle.
E
F
O
O est le centre du cercle, E et F sont deux points du cercle.
est un angle au centre du cercle (C).
FOE 
FOE 
Cet angle intercepte l’arc EF.
Remarque : il n’y aqu’un seul
angle au centre de ce cercle
qui intercepte l’arc EF.
Fabienne BUSSAC

b. Propriétés
Si dans un cercle, un angle inscrit et un angle au centre interceptent
le même arc, alors l’angle inscrit mesure la moitié de l’angle au
centre.
A
B
O
M
(C) est un cercle de centre O.
L’angle
BMA ˆ
est inscrit dans le cercle.
L’angle
BOA ˆ
est un angle au centre
du cercle.
Ces deux angles interceptent le
même arc AB.
Donc :
BMABOAou
BOA
BMA ˆ 2
ˆ
2
ˆ
ˆ
Fabienne BUSSAC

Conséquence : Si, dans un cercle, deux angles inscrits interceptent le
même arc, alors ils ont la même mesure.
A
B
O
MN
(C) est un cercle de centre O.
Les angles
BMA ˆ
sont inscrits dans le cercle, etet
BNA ˆ
interceptent le même arc AB.
Ils mesurent tous les deux la
moitié de l’angle au centre
BOA ˆ
qui intercepte l’arc AB
donc ils ont la même mesure.
BMA ˆ
=
BNA ˆ
Fabienne BUSSAC

2. POLYGONES REGULIERS
Un polygone régulier est un polygone qui a tous ses côtés de
même longueur et tous ses angles de même mesure.
Tous les sommets d’un polygone régulier appartiennent à un
même cercle : on dit qu’il est inscrit dans le cercle. Le centre du
cercle est appelé centre du polygone.
Exemples : Le triangle équilatéral, le carré… mais pas le losange.
Dans un polygone, de centre O, àncôtés, si Aet B sont deux
sommets consécutifs alors l’angle
BOA ˆ
est appelé angle au
centre du polygone et sa mesure est égale à
n
360
Fabienne BUSSAC