Aucun titre de diapositive

Filtrage - Modulation 49
MODULATION
III - Modulation de fréquences
Généralités
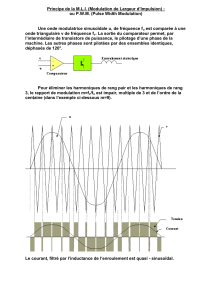
Les modulations de fréquence ou de phase sont appelées des modulations
d’angle. La modulation due au signal s(t) agit de manière linéaire sur
l’argument de la fonction harmonique formant le signal porteur.
Les composantes spectrales de l’onde modulée dépendent aussi bien de
la fréquence que de l’amplitude du signal modulant (s(t)).
Cette définition nous conduit aux deux types de modulations suivantes :
)(2cos)(2cos)( 000 tsktfttftsm
t
FmF dsktfttfts
)(22cos)(2cos)( 00
Modulation de phase :
Modulation de fréquence :

Filtrage - Modulation 50
MODULATION
Calculons la fréquence instantanée du signal modulé :
dttds
k
f
dt
tsktfd
tfts im )(
22
)(2
)()( 0
00
)(
2
)(22
)()( 0
0tskf
dt
dsktfd
tfts F
t
F
imF 
Modulé le terme porteur par ds/dt à l’aide de la modulation de phase ou le
moduler par s(t) à l’aide d’une modulation de fréquence revient au même.
Cette propriété est due au fait que :
dt
d
tfi
2
1
)( 
Remarquons que les constantes kFet kF, appelées pente de modulation
s’expérimentent avec des unité différentes : kF~rd/V et kF~Hz/V

Filtrage - Modulation 51
MODULATION
Remarque :
Intégrateur
s(t) Signal modulé
en fréquence
Modulateur de phase
Dérivateur
s(t) Signal modulé
en phase
Modulateur de fréquence
dt
d
tskftf Fi
2
1
)()( 0
dsktft t
F
 )(22)( 0
t
FmF dsktftts
)(22cos)(cos)( 0
Déterminons le taux de modulation dans le cas d’un signal borné :
|s(t)| M

Filtrage - Modulation 52
MODULATION
|s(t)| M : f0-kFM fi(t) f0+kFM
Taux de modulation (Profondeur) : Df/f0(relatif à f0), l’indice de modulation
est le rapport de kFM à la fréquence la plus haute de S(f), supposé à bande
limitée [-fM, fM] :
M
F
fMk
:modulationdeIndice
|s(t)| M: |s’(t)| 2MfM: f0-kFfMM fi(t) f0+kFfMM
dt
d
dttds
k
ftfi
2
1)(
2
)( 0
)(2)( 0tsktft
Mk :modulationdeIndice
Remarque : s(t)=Acos(2Ft) (M=A et fM=F)
•MF : sMF(t) = cos(2f0t+mFsin(2Ft))
•MF: sMF(t) = cos(2f0t+mFcos(2Ft))

Filtrage - Modulation 53
MODULATION
)2cos()(: 0FtAkftfMF Fi
Akf F D
Remarque : s(t)=Acos(2Ft) (M=A et fM=F)
)2sin(2)( 0Ft
F
Ak
tft F
F
M
Fm
ff F
Ak  D
)2sin(2cos)( 0Ftmtfts FMF
)2sin()(: 2
2
0FtftfM FAk i
AFkf D
)2cos(2)( 0FtAktft
m
ff
Ak
M
D
)2cos(2cos)( 0FtmtftsM
On remarque que dans le cas de la modulation de fréquence, la déviation fi
autour de f0est bornée par une valeur kF qui ne dépend que de la valeur
maximale de s(t) (soit s(t) M) et ne dépend pas de la fréquence F de s(t)!