Application des lois de Newton et Lois de Kepler v

Chapitre 11
Application des lois de Newton et Lois de Kepler
1
1. Mouvement dans un champ de pesanteur uniforme
1.1. Champ de pesanteur
La pesanteur se faisant ressentir dans tout l’espace autour de la Terre, on dit qu’il existe un champ de pesanteur.
Ce champ est vectoriel puisqu’en chaque point, il a une valeur, une direction et un sens.
Définition : Au voisinage de la Terre, le vecteur champ de pesanteur  en un point où se trouve une masse m (en kg)
est défini par :
 avec  le poids (en N) de la masse m
Caractéristiques de  :
• Direction : ……………………………………………………………….
• Sens : ……………………………………………………………………….
• Valeur ou intensité de la pesanteur : g = 9,8 N/kg à la surface de la Terre
Propriétés :
Localement (si les dimensions n’excèdent pas quelques km), le champ de pesanteur est considéré comme ……………..
Le vecteur  y a alors le ………………………….. en direction, sens et intensité en tout point.
1.2. Chute sans frottement : chute libre
1.2.1. Définition :
Définition : …………………………………………………………………………………………………………………………………………………………….
1.2.2. Analyse physique
• Le système étudié est un objet de masse m et de centre d’inertie G.
• Il est lancé au voisinage de la Terre avec une vitesse initiale
0
v
.
• Le référentiel d’étude est le ……………………………………………..
supposé galiléen.
• Dans le domaine du lancer, le champ de pesanteur est
considéré comme ……………………………………
• Forces extérieures appliquées au système : ……………………………
On néglige la force de frottement fluide et la poussée
d’Archimède.
On se retrouve dans le cas ………………………………………………
D’après la deuxième loi de Newton :
Constante k
a t + b
a t
2
+ b t + c
sa dérivée donne :
une primitive donne :
i
r
k
O
z
x
0
v
α
G
0
x
0
z
0
⊗
j
S
portée
P

Chapitre 11
Application des lois de Newton et Lois de Kepler
2
1.2.3. Equation horaires du vecteur accélération :
Dans le repère d’espace orthonormé (O,
k,j,i
), la projection de la relation vectorielle
G
a
=
g
donne :
=
=
=
)t(a
)t(a
)t(a
z
y
x
1.2.4. Conditions initiales
Dans le repère d’espace orthonormé (O,
k,j,i
)
Conditions initiales : Supposons qu’à l’instant t = 0, le point matériel G est lancé de G
0
avec une vitesse initiale 
faisant un angle α avec l’axe Ox.
x(0) =
Le vecteur position initiale s’écrit alors  y(0) =
z(0) =
v
0x
=
Le vecteur vitesse initiale a pour coordonnées :  v
0y
=
v
0z
=
1.2.5. Equations horaires du vecteur vitesse
)t(a
G
=
dt
)t(dv
G
donc
=
=
=
dt
)t(dvdt
)t(dvdt
)t(dv
z
y
x
et par intégration des équations horaires du vecteur accélération, on obtient :
=
=
=
)t(v
)t(v
)t(v
z
y
x
On détermine les constantes à l’aide des conditions initiales :
Equations horaires du vecteur vitesse :
Lors d’une chute libre avec une vitesse initiale située dans le plan (x0z) et formant un angle α avec l’axe (Ox), les
coordonnées du vecteur vitesse du centre d’inertie du solide sont :
=
=
=
)t(v
)t(v
)t(v
z
y
x
Le mouvement est ……………………………. selon l’axe Ox et ………………………………………………………………. selon l’axe Oz.
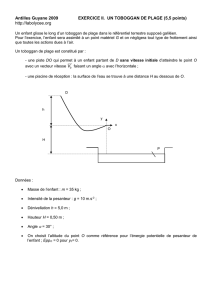
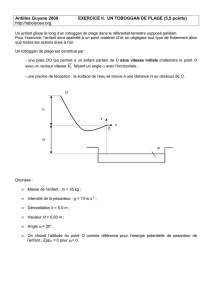
Fig 2 : Vecteur vitesse

Chapitre 11
Application des lois de Newton et Lois de Kepler
3
1.2.6. Equations horaires du vecteur position :
dt
)t(OGd
)t(v
G
= donc
=
=
=
dt
)t(dzdt
)t(dy
dt
)t(dx
et par intégration des équations horaires du vecteur vitesse, on obtient : x(t)=
y(t)=
z(t)=
On détermine les constantes à l’aide des conditions initiales :
Equations horaires du vecteur position :
Lors d’une chute libre avec une vitesse initiale située dans le plan (x0z) et formant un angle α avec l’axe (Ox), les
coordonnées du vecteur position du centre d’inertie du solide sont :
=
=
=
)t(z )t(y )t(x
Remarque : Comme y(t) = 0, le mouvement s’effectue dans le plan
……………………..
1.2.7. Equation de la trajectoire
L’équation z = f(x) est celle de la trajectoire du centre d’inertie G du système. Elle
s’obtient en éliminant t entre x(t) et z(t).
(1) devient t =
)cos(v
)t(x
0α
, que l’on reporte dans l’expression de z(t). On
obtient ainsi l’équation de la trajectoire.
z(x) =
L’équation de la trajectoire z(x) =
est celle d’une parabole dont la concavité est tournée vers le bas.
Remarque : Déterminer la flèche c'est calculer l'altitude maximale atteinte
par le projectile.
Fig 3 : a) Influence de la vitesse
b) Influence de l’angle

Chapitre 11
Application des lois de Newton et Lois de Kepler
4
2. Mouvement d’une particule chargée dans un champ électrostatique uniforme
2.1. Champ électrostatique E et force électrique (Voir cours de 1ère S)
• Un champ électrostatique  s’obtient entre deux armatures métalliques planes P et N
séparées d’une distance d, entre lesquelles une tension U
PN
est appliquée.
Remarque : Un champ électrostatique  uniforme a même valeur, même direction,
même sens en tout point de l’espace
• Une particule chargée de charge électrique q dans un champ électrostatique 
subit une force  telle que :
F en N ; E en V.m
-1
et q en C (Coulomb)
2.2. Analyse physique
• Une particule chargée de masse m et de charge électrique q pénètre avec une
vitesse initiale  dans une région où règne dans un champ électrostatique uniforme  .
• Système étudié : ……………………………………………………………
• Référentiel : …………………………………………………………………………………………………
• Forces extérieures appliquées au système :
- ……………………………………………………………………….
- …………………………………………………………………………
Exercice : 20 p 176
D’après la deuxième loi de Newton :
Σ  = m . 
= m . 
q  = m .  d’où  =
2.3. Equations horaires du vecteur accélération
Dans le repère d’espace orthonormé (O, k,j,i ), la projection de la relation vectorielle
G
a
= donne :
a
x
(t) =
a
y
(t) =
a
z
(t) =
Caractéristiques du champ électrique :
- Direction : ……………………………………………………………………………………………………
- Sens : ………………………………………………………………………………………………………
………………………………………
- Norme : E en V.m
-1
; U
PN
en V ; d en m

Chapitre 11
Application des lois de Newton et Lois de Kepler
5
2.4. Conditions initiales
Dans le repère d’espace orthonormé (O, k,j,i )
Conditions initiales : Supposons qu’à l’instant t = 0, la particule chargée est lancé de O avec une vitesse initiale 
faisant un angle α avec l’axe Ox.
x(0) = 0
Le vecteur position initiale s’écrit alors  y(0) = 0
z(0) = 0
v
0x
= v
0
cos α
Le vecteur vitesse initiale a pour coordonnées :  v
0y
= 0
v
0z
= v
0
sin α
2.5. Equations horaires du vecteur vitesse
)t(a
G
=
dt
)t(dv
G
donc
=
=
=
dt
)t(dvdt
)t(dvdt
)t(dv
z
y
x
et par intégration des équations horaires du vecteur accélération, on obtient :
=
=
=
)t(v
)t(v
)t(v
z
y
x
On détermine les constantes à l’aide des conditions initiales :
Equations horaires du vecteur vitesse : avec une vitesse initiale située dans le plan (x0z) et formant un angle α avec
l’axe (Ox), les coordonnées du vecteur vitesse du centre d’inertie de la particule chargée placée dans un champ
électrostatique sont :
=
=
=
)t(v
)t(v
)t(v
z
y
x
Le mouvement est uniforme selon l’axe Ox et uniformément varié selon l’axe Oz.
2.6. Equations horaires du mouvement
dt
)t(OGd
)t(v
G
= donc
=
=
=
dt
)t(dzdt
)t(dy
dt
)t(dx