pcetoileexosphysrevispcsi ( PDF - 548.5 ko)

PC* Révisions Physique de première année 1 Enoncés
PC * Physique
Bienvenu en PC* du Lycée Cézanne !
Le programme de Physique de la filière PC-PC* est moderne et très riche, en phase avec les
développements technologiques actuels dans les secteurs de pointe. Voici son déroulé :
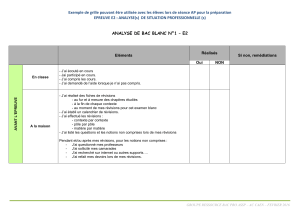
Cours Travaux pratiques
Compléments de mécanique du point et du solide 3 semaines
Mécanique des fluides et thermodynamique 7 semaines
Ondes mécaniques, acoustique 4 semaines
Electronique et traitement du signal
Optique ondulatoire 4 semaines
Electromagnétisme 5,5 semaines
Mécanique quantique 1,5 semaine
Optique et ondes
Ce programme est aussi très lourd, alors que l’année est très courte : à cause des concours, elle s’arrête
vers le avril. En particulier, on ne dispose pas du temps nécessaire pour réviser le cours de première
année. C’est donc à vous d’effectuer vous-même ces révisions. Comme le cours de deuxième année PC *
commencera par de la Mécanique, et les premiers Travaux Pratiques par de l’Électronique, il est
fortement conseillé de revoir les chapitres correspondants de programme de première année.
Pour vous y aider, voici quelques exercices sur ces questions …
Les solutions … sont cachées sur le site du Lycée Cézanne, dans la page PC* !
Et n’oubliez pas les TIPE dont le thème de l’année est : Optimalité : choix, contraintes, hasard.
A] Exercices d’électronique sur le programme PCSI
Ex.1) Énergie photovoltaïque
Voici la caractéristique d’une cellule
photovoltaïque (ou panneau solaire) de
surface S placée en plein soleil :
1) Quels adjectifs (électrocinétiques …)
peuvent s’appliquer à cette cellule ?
2) Quel nom donner à 0
U ? à 0 I ? Comment faire pour les mesurer ?
Pour une cellule de dimension 30 cm X 30 cm, on mesure 0
U=
12 V et 0
I= 1,0 A … en plein soleil : 0 Uest constante,
indépendante de l’éclairement, mais 0
I, proportionnel à
l’éclairement, diminue avec l’éclairement, noté E ici.
3) On branche sur cette cellule une résistance R.
a) Donner le schéma du montage .
b) Quelle valeur faut-il choisir pour R si l’on veut que R reçoive la puissance maximale que peut fournir
la cellule en plein soleil ?
c) Comment au contraire doit-on choisir R si l’on souhaite que la puissance reçue par R ne change pas si
l’éclairement diminue (un peu) par rapport au plein soleil ?
4) On peut associer à volonté ces panneaux solaires.
On souhaite les utiliser dans un lieu isolé pour alimenter une pompe de puisage destinée à l’irrigation, sur
laquelle figure les indications suivantes : 120 V ; 2,5 A.
Comment associer ces cellules, et de combien en a-t-on besoin ?
I
I
0
U
0
U
0
U
I
I
I
0
(E
1
)
U
0
U
0
I
0
(E
2
)
(E
1
> E
2
)

PC* Révisions Physique de première année 2 Enoncés
Ex 2) Internet bas débit. On considère le montage suivant :
• Pour t < 0, e(t) = 0 ; toutes les intensités sont nulles et la capacité
C est déchargée.
• Pour t > 0, e(t) = E.
1)a) Pour t > 0, établir l’équation différentielle vérifiée par
)(tu
b) On a : L = 0,1 mH et C = 2,5 nF. Déterminer la valeur à donner
à R pour que le basculement de u(t) de 0 à sa valeur limite soit le
plus rapide possible.
2) Ce montage est une modélisation simple de l’internet bas débit :
e(t) représente le serveur, L et C la ligne téléphonique et R le
modem. Le serveur délivre des « bits », créneaux de durée T, d’amplitude +E (c’est le bit « 1 ») ou –E
(c’est le bit « 0 »). Ainsi :
e(t)
E
T/2 T/2
T
t
1 1 0
Le serveur vient d’émettre la séquence 11010
Voici, selon les valeurs de T, l’allure du signal u(t) transmis par la ligne, et reçu par le modem, pour un
bit « 1 » :
a) En s’intéressant simplement à la montée (t < 0, e(t) = 0 ; toutes les intensités sont nulles et la
capacité C est déchargée et pour t > 0, e(t) = E), donner la loi u(t) si R a été choisie de façon optimale
comme au 1) b).
b) En déduire une évaluation de la condition sur la durée T pour que le bit soit bien transmis.
c) Les données ci-dessus de L et C sont relatives à une ligne téléphonique de longueur l = 1 km.
Quel débit maximum, en bits par seconde, puis kilooctets par seconde, peut assurer cette ligne ?
d) Mais si la ligne a une longueur l’ = n km, son inductance est L’ = n.L et sa capacité C’=n.C.
La résistance du modem et le débit maximum dépendent-ils de la longueur de la ligne, et comment cela ?
Pourquoi internet fonctionne-t-il mal à la campagne ? Qu’est-ce qu’un « répétiteur » : dispositif que
l’opérateur réseau doit placer régulièrement sur les longues lignes pour en améliorer le fonctionnement ?
Le bit est bien transmis
Limite
Echec : T est trop court, le modem n’a pas pu détecter le « 1 »
serveur
R
L
e(t)
u(t)
C
modem ligne téléphonique

PC* Révisions Physique de première année 3 Enoncés
Ex.3) Voici six filtres :
R
C e s
Filtre (a)
R
C
e s
Filtre (b)
R
C e
R
C s
Filtre (aa)
R
C
e
Filtre (bb)
R
C s
R
C e
Filtre (ab)
R
C s R
C s
R
C
e
Filtre (ba)
1) Indiquer sans calculs :
a) la nature (passe-haut, passe-bas, …) de chacun de ces filtres
b) leur ordre.
2) Voici les diagrammes de Bode en gain qu’on obtient (toutes les R et toutes les C ont les mêmes
valeurs), rangés dans le plus grand désordre. Indiquer la correspondance entre le filtre et le diagramme.
Quelle est la valeur du produit RC ?
diagramme n°1 diagramme n°2

PC* Révisions Physique de première année 4 Enoncés
3) Les diagrammes n°3 et 4 semblent être les mêmes : le montrer, par le calcul des fonctions de transfert
des filtres concernés.
4) On alimente ces filtres par une tension d’entrée en créneaux, d’amplitude 1 V. Voici un exemple des
oscillogrammes obtenus :
Pour chaque oscillogramme, quel a été le filtre utilisé ?
diagramme n°4
diagramme n°3
diagramme n°6 diagramme n°5
f = 300 Hz f = 30 kHz

PC* Révisions Physique de première année 5 Enoncés
Ex.4) Filtre d’accord d’un poste radio.
On rappelle la forme normalisée de la fonction de transfert du
2ème ordre passe-bande :
)(1
)(
1
1
)(
)(
0
0
2
00
0
jQ
A
jj
Q
j
Q
A
jH
Le filtre d’accord est réalisé de la façon suivante, où L et/ou C
sont réglables :
Si une station radio émet à la pulsation ω, l’antenne est
parcourue par une intensité tIt M
cos)( . Le filtre d’accord
transforme cette intensité en une tension s(t) qui sera ensuite amplifiée puis traitée par le poste récepteur.
1) IM et ω étant données, comment faut-il choisir L et C de façon à ce que l’amplitude de s(t) soit
maximale ? Quelle est la largeur de la bande passante ?
L’antenne d’une radio capte toutes les émissions en même temps ; physiquement, les différentes stations
diffèrent les unes des autres par leur fréquence (de porteuse). L’auditeur désire évidemment n’écouter
qu’une seule station en même temps ! La première des choses à faire est donc de filtrer le signal
électrique délivré par l’antenne (contenant la superposition de toutes les émissions) pour ne sélectionner
que l’émission souhaitée.
Une station donnée (appelons-la la station (1)) délivre dans
l’antenne le courant (c’est de la modulation d’amplitude) :
1(t) = I01.[ 1 + m1.cos(ω1t)].cos(Ω1t)] (où 0 < m1 < 1)
● m1.cos(ω1t) représente le signal sonore (la musique,
p.e.) qui réalise la modulation d’amplitude; m1 et ω1 sont
(lentement) variables dans le temps ; on rappelle que les
fréquences audibles sont comprises dans l’intervalle [20 Hz,
20 kHz] : ω1 est ici la pulsation de la musique.
● I01.cos(Ω1t) est la « porteuse » : la fréquence de
porteuse est F1  qqs 100kHz, elle est fixe dans le temps.
Comme il y a n stations, l’antenne délivre en fait le courant
n
k
ktt
1
)()(
2) On suppose que l’antenne ne reçoit qu’une seule station qui y délivre :
1(t) = I01.[ 1 + m1.cos(ω1t)].cos(Ω1t)] où on rappelle : ω1 << Ω1 (qqs kHz << qqs 100 kHz)
a) Quelles sont les différentes fréquences contenues dans
1(t)? On rappelle :
)cos()cos(
2
1
cos.cos abbaba 
b) Quelle valeur doit-on choisir pour la fréquence de résonance F0 du filtre de façon à obtenir une
bonne réception de cette station (1) ?
c) Quelle largeur en fréquence devrait avoir la bande passante du filtre pour que ce poste ait une
qualité sonore convenable ?
d) Rappeler l’expression de la largeur de la bande passante de ce filtre d’accord. Relativement à
cette caractéristique, sur quel composant (L ou C ?) a-t-on intérêt à agir pour réaliser l’accord ?
e) La station voisine a la fréquence de porteuse F2 > F1 : à quelle condition est-elle rejetée par le
filtre ?
R
L
C
η(t)
s(t)
Antenne
Filtre
d’accord
(t)
Enveloppe :
I0[1+mcos(Ωt)]