TP n°2 : Quelques caractéristiques d`un son musical

TP-cours de physique n°2 : Quelques caractéristiques d'un son musical
I.
Son pur et son complexe
1) Cas d'un diapason :
On place un microphone juste devant l’ouverture de la caisse de résonance du diapason. On relie le
microphone à l'interface ESAO4. On enregistre, via l’interface et le logiciel d’acquisition « Atelier
scientifique Physique-Chimie », le son émis par le diapason frappé. On obtient le graphique suivant avec
le signal électrique correspondant au son du diapason :
a) Est-ce que l'onde sonore émise par le diapason est périodique ? Est-elle sinusoïdale ?
Si l'onde sonore est périodique et sinusoïdale, le son est dit pur.
Si elle n'est que périodique, le son est dit complexe.
b) Est-ce que l'enregistrement associé au diapason correspond à un son pur ? à un son complexe ?
c) Déterminez, en expliquant, la période Td de l'onde sonore issue du diapason, puis la fréquence fd
associée. On n’oubliera pas d’être précis…
2) Cas d’un instrument de musique :
 Récupérez un instrument de musique auprès du professeur (instrument que l’on nommera ou décrira).
 Placez le microphone (à l’aide éventuellement du professeur) à un endroit adéquat afin de pouvoir
ensuite enregistrer un son émis par l’instrument. Reliez le microphone à l'interface ESAO4.
On souhaite enregistrer via l’interface et le logiciel d’acquisition « Atelier scientifique Physique-Chimie
», le son émis au cours du temps par l’instrument de musique (lorsque tous les trous sont bouchés si
plusieurs notes de musique peuvent être jouées).
 Paramétrez le logiciel d’acquisition en conséquence. On prendra comme durée d’acquisition : 50 ms
et comme nombre de points : 1000. On n’oubliera pas, grâce à l’onglet « Affichage », de faire en sorte
que les points soient reliés.
 Faîtes l’enregistrement correspondant au son émis (après stabilisation du son) et visualisez le
graphique obtenu (l’extrémité de l’instrument en contact avec la bouche doit être nettoyé après
chaque demi-groupe !).
a) Est-ce que l'onde sonore émise par l’instrument est périodique ? Est-elle sinusoïdale ?
b) Est-ce que l'enregistrement associé à l’instrument correspond à un son pur ? à un son complexe ?
c) Déterminez, en expliquant, à l'aide de la fonction « Pointeur » du menu « Outils » du logiciel, la
période T du signal, puis la hauteur du son associée.
d) Quel dispositif produit le son le plus grave : le diapason ou l’instrument utilisé ensuite (tous les
trous étant bouchés) ? Justifiez.
Le mathématicien Joseph Fourier (1768 - 1830) a montré qu'un signal périodique peut être décomposé en
une somme de signaux sinusoïdaux. Dans le cas d'une onde sonore, un son complexe peut donc être
décomposé en une somme de sons purs ; ces sons purs sont alors appelés des harmoniques.
Fourier a également montré que les fréquences des harmoniques sont des multiples de la fréquence du
signal périodique, c'est-à-dire ici, du son complexe. Ainsi, pour un harmonique de rang n, on a la
fréquence : fn = n×f (n entier ≥ 1). Un son complexe ne possède pas tous les harmoniques possibles et
imaginables ! D'ailleurs, les harmoniques de certains sons n'ont pas des rangs consécutifs...
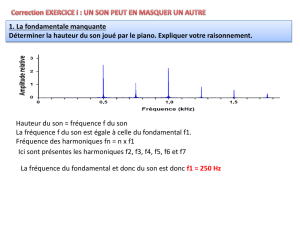
Le logiciel « Atelier scientifique Physique-Chimie » est capable de réaliser une analyse spectrale d'un son
enregistré, c'est-à-dire d'afficher la décomposition du son : le spectre du son. On y voit l'importance
relative de chaque harmonique et les fréquences de ceux-ci.
 Cliquez sur « Traitement des données », sélectionnez ensuite « Transformée de Fourier ».
 Complétez les différents champs et obligatoirement : « Grandeur à sélectionner » et « Intervalle » : il
s’agit d’un intervalle correspondant à une période.
 Cliquer sur « Tracer » pour obtenir le spectre du son enregistré.
 Imprimez sur une seule page : le signal correspondant au son enregistré et le spectre de ce son.
e) Comparez f à la fréquence f1 correspondant à la fréquence du 1er harmonique à gauche
(harmonique de rang 1).
L'harmonique de rang 1, associé à la fréquence du signal f (hauteur), est aussi appelé le fondamental.
f) Déterminez les fréquences associées aux 4 harmoniques suivants (s’il y a moins de 4
harmoniques, déterminez les fréquences de tous les harmoniques).
g) Est-ce que l'expression fn = n×f est vérifiée pour ces premiers harmoniques ? Justifiez.
II.
Timbre d'un son
1) Définition :
Le timbre d'un son est propre à chaque instrument de musique, c'est ce qui permet de différentier à
l'oreille une même note de musique jouée (même hauteur de son) par des instruments différents. Le
timbre d'un son est lié en partie au nombre d'harmoniques présents et à leur amplitude respective
(composition spectrale). Il dépend aussi de l'évolution du son au cours du temps (enveloppe du son).
2) Etude de l'enveloppe d'un son musical :
L'enveloppe d'un son se décompose généralement en 3 parties :
 L'attaque du son : c'est la montée en amplitude de la vibration sonore au début de l'émission.
 Le corps est la phase entre l'attaque du son et son extinction.
 L'extinction est la phase pendant laquelle l'amplitude de la vibration diminue avant de s'annuler, à la
fin de l'émission.
L'attaque et l'extinction constituent les phases transitoires du son.
 Sélectionnez le logiciel « Audacity », puis ouvrez, grâce à celui-ci, deux des fichiers parmi les
suivants « violon.wav », « guitare1.wav », « guitare2.wav », « flûte.wav » ou « basson.wav » (à
l’intérieur du dossier « sons TP »).
a) Notez les noms des deux fichiers sélectionnés.
b) A l’aide de la visualisation de l’enveloppe des sons et de leur écoute (casque audio fourni ou
propre casque), comparez l’attaque et l’extinction des sons associés aux 2 fichiers sélectionnés
(pour utiliser « Audacity », on pourra s'aider de la fiche méthode fournie).
c) *Est-ce que ces deux fichiers correspondent à la même note de musique ? Expliquez la méthode.