correction

1. La fondamentale manquante
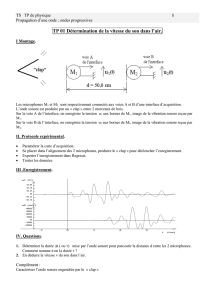
Déterminer la hauteur du son joué par le piano. Expliquer votre raisonnement.
Hauteur du son = fréquence f du son
La fréquence f du son est égale à celle du fondamental f1.
Fréquence des harmoniques fn = n x f1
Ici sont présentes les harmoniques f2, f3, f4, f5, f6 et f7
La fréquence du fondamental et donc du son est donc f1 = 250 Hz

Le niveau sonore est L = 40 dB
Niveau sonore :
L= 10 x Log ( I/Io)
Intensité sonore :
I = Io x 10L/10
I = 10-12 x 10 40/10 = 10-8 W/m²
2.2. En étudiant chaque pic du spectre de la figure 3, indiquer celui ou ceux
qui seront éliminés par ce codage MP3. Justifier.
2. L’effet de masquage
2.1- Déterminer l’intensité sonore minimale pour qu’un son de fréquence 800 Hz
soit audible en présence d’un son masquant de fréquence 1 kHz et de niveau sonore 55
dB.
Fréquence f1 = 440 Hz L = 28 dB Lmini = 8dB
Fréquence f2 = 880 Hz L = 35 dB Lmini = 50dB
Fréquence f3 = 1320 Hz L = 50 dB Lmini = 20dB
Fréquence f4 = 1760 Hz L = 35 dB Lmini = 15dB
Donc la fréquence f2=880 Hz sera masquée.

2.3. Effet de masquage lors du passage d’un train
Si l’orateur ne parle pas plus fort mais se rapproche de l’auditeur, à quelle distance de
l’auditeur devra-t-il se placer pour être audible ? Justifier les étapes de votre
raisonnement.
« L’auditeur perçoit la parole de l’orateur avec un niveau d’intensité sonore égal à 50 dB à
un mètre . »
I =Io x 10L/10 = 10-12 x 10 50/10 = 10 -7 W/m² I = k/d² = k/1² = k donc k = 10-7 W
« le niveau d’intensité sonore minimal audible de la parole, en présence du train, est
égal à 60 dB quelle que soit la fréquence. »
I = 10-12 x 10 60/10 = 10 -6 W/m² I = k/d²
Donc d² = k/I = 10-7/10-6 = 0.1 m² donc d = 0.1 = 0.32 m
Donc l’auditeur devra se placer à une distance inférieure à 32 cm pour être audible.

1- Quel phénomène physique observe-t-on au passage de ce détroit ? Justifier
l’existence de ce phénomène par un calcul .
On observe donc un phénomène de diffraction d’une onde par une fente dont la
largeur doit être du même ordre de grandeur que la longueur d’onde des vagues.
Vérification :
λ = v x T = 170 x (50x60) = 510 km Calcul de la longueur d’onde :
Largeur du détroit : 180 km
Longueur d’onde : 510 km Même ordre de grandeur ( la centaine de km)

2.1- Trouver la profondeur moyenne de la mer d’Andaman vers le nord (axe Oy).
Y = f(t) linéaire donc
y = v x t
( v coefficient directeur de la
droite)
Mesure sur le graphe :
V = = 150 m/s
6x105
4000
V = g x h
V² = g x h
Donc h = =
V²
g
150²
9.8 = 2300 m