EXERCICES DE MECANIQUE

EXERCICES DE MECANIQUE
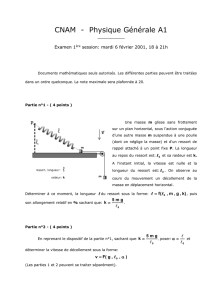
Exercice 1 : Une tige homogène AB , de
masse m = 1,5 kg , peut tourner autour d’un
axe horizontal passant par A .
Au centre de gravité G , on fixe un ressort R
horizontal, de raideur k = 20 N.m-1 et de
longueur au repos l0 = 18 cm . A l’équilibre
(comme l’indique la figure) la longueur du
ressort vaut l = 43 cm .
1. Déterminer l’intensité F de la force
exercée par le ressort sur la tige AB .
2. Déterminer la réaction de l’axe de rotation sur la tige et la valeur de l’angle α .
Exercice 2 : Une porte de masse m = 50 kg , de
dimensions rectangulaires : a = 205 cm b = 83 cm
tourne autour de l’axe AB .
Cet axe repose au point B dans un support et est guidé
au point A par une charnière de petite dimension. On
néglige tout frottement
Calculer les intensités des réactions en A et en B sur
la porte
Exercice 3 :
Une potence porte en F une
charge de masse M = 200 kg .
On néglige le poids des barres AD, CF et BE devant le poids de
la charge .
Cette potence repose en A dans un support et est maintenue en
D par une charnière, tout cela sans frottement.
Les dimensions de la potence sont :
AB = CD = EF = a et BC = CE = 2a
Déterminer les intensités des réactions sur la potence en A et
en D .
Exercice 4 : Une roue, de diamètre D = 60 cm, peut tourner
autour d’un axe horizontal, passant par O .
Aux points A1 et A2 , on suspend des masses comme
l’indique la figure :
m1 = 200 g m2 = 50 g OA1 = 25 cm α = 30 °
1. La roue est-elle immobile ?
2. Sinon, quelle est l’intensité F et le sens de la force
horizontale qu’il faut appliquer en B pour que la
roue soit en équilibre ?
A
B
G R
α

Exercice 5 : Une barre rigide AB , de longueur AB = 2L et de masse m = 2 kg peut
tourner dans un plan vertical (plan de la figure) et autour
d’un axe horizontal (∆) passant par le point A .
Cette barre est maintenue par un fil inextensible, de masse
négligeable . Dun côté ce fil est attaché en K et de l’autre
côté au centre de gravité G de la barre.
La barre est en équilibre et on constate que :
α = 30° et β = 60°
Déterminer : 1. La tension du fil
2. La réaction de l’axe en A .
Exercice 6 : Une voiture roule à la vitesse de 125 km/h sur une route horizontale. La
résistance dûe à l’air vaut Ra = 800 N et la résistance au roulement vaut 2% du poids .
La masse de la voiture vaut m = 1000 kg .
1. Faire un schéma du bilan des forces.
2. Déterminer la valeur Fm de la force motrice de la voiture.
3. Calculer la puissance développée par la voiture.
Exercice 7 :
1. Un cycliste, de masse m = 80 kg , dévale une pente de 12% (12 m de dénivelé pour
100 m de déplacement horizontal) .
Il est en roue libre (il « n’appuie pas » sur les pédales) et sa vitesse vaut v = 90 km/h .
a. Calculer la valeur de la résultante de tous les frottements.
b. Calculer le travail du poids WP
P et le travail des forces de frottements Wf sur un trajet
de x = 100 m .
c. Calculer l’énergie cinétique Ec du cycliste.
2. La route est maintenant horizontale et le cycliste roule à la vitesse de v’ = 54 km/h .
Les différents frottements sont équivalents à une force f’ = 100 N . Un spectateur surgit
alors devant le cycliste qui est obligé de freiner violemment . Il arrive à s’arrêter au bout de
d = 20 m . Calculer l’intensité de la force de freinage Ff .
Exercice 8 : Une voiture de masse m = 950 kg , peut rouler à la vitesse v1 = 120 km/h sur
route horizontale et à la vitesse v2 = 100 km/h sur une route en pente montante de 5%.
La résistance au roulement vaut Rr = 15% du Poids et la résistance dûe à l’air est
proportionnelle au carré de la vitesse .
Calculer la puissance Pm de la voiture.
Exercice 9 : Un solide S , de masse m = 300 g ,
est fixé à un ressort de raideur k = 30 N.m-1 .
On provoque une compression du ressort de 8 cm
et on lâche le système sans vitesse initiale. On néglige les frottements .

Calculer :
1. L’intensité de la force T exercée par le ressort à l’instant de départ.
2. L’énergie mécanique Em du système .
3. La vitesse v1 de S quand le ressort est étiré de 2 cm .
Exercice 10 : Une pierre, de masse m = 20 kg , tombe d’une falaise de hauteur H = 20 m.
On considère que les frottements dûs à l’air sont négligeables. On prendra l’origine des
potentiels au pied de la falaise .
Calculer :
1. L’énergie mécanique de la pierre
2. L’énergie potentielle et l’énergie cinétique pour une altitude :
a. z1 = H/2 b. z2 = H/4
Exercice 11 : L’énergie potentielle élastique d’un ressort vaut 0,1 J . Si on provoque un
allongement supplémentaire de 4 cm , cette énergie prend la valeur de 0,9 J .
Calculer :
1. La raideur k du ressort utilisé
2. L’allongement initial du ressort.
Exercice 12 :
1. Une masse m = 50 g est
accrochée à un ressort . Ce ressort
est comprimé de xm = 10 cm , puis
lâché sans vitesse initiale . Lorsqu’il se détend, la vitesse maximale atteinte par la masse
m vaut vm = 3,0 m/s . Il n’y a pas de frottements.
Déterminer la raideur k du ressort .
2. Quand le ressort est étiré de x1 , la masse m possède une vitesse dont la valeur
algébrique vaut v1 = + 1,5 m/s . Il n’y a pas de frottements. Calculer x1 .
3. Alors que la masse a atteint la vitesse v2 = - 2,0 m/s , elle se décroche du ressort
(en situation d’étirement).
3.1. Quelle sera le mouvement de la masse en supposant qu’il n’ y a pas de
frottements .
3.2. En réalité , au moment où la masse se décroche, elle est soumise tout le long de
son mouvement par une force de frottements f . Sachant que la masse
s’arrête au bout d’une distance d = 2,5 m , calculer l’intensité f de cette force .
Exercice 13 : Sur un plan AB , incliné d’un angle α = 30° sur l’horizontale, on lance un
solide S (m = 10 kg) vers le haut avec une vitesse initiale vA = 8 m.s-1 . Le solide parcourt
une distance AB = d = 5 m avant de s’arrêter. Puis il redescend .
1. L’énergie mécanique est-elle constante ? Expliquer.
2. En déduire la valeur numérique f des forces de frottements
3. Calculer la vitesse vA’ du solide S lorsqu’il repasse par le point A en descendant.
On considère que les frottements sont ceux calculés précédemment .