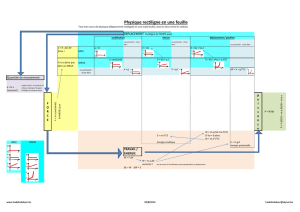
1. Cinématique MRU MRUA Fichier

1
Rémy Maire 2015 - 2016
1. CINEMATIQUE cours
0. Introduction
La cinématique étudie la description du mouvement des objets mais sans traiter les causes
qui font déplacer ces objets.
Les notions qui seront abordées au cours de ce chapitre, sont les suivantes:
□ mesure du temps
□ système et référentiel
□ trajectoire d’un point
□ vitesse d’un point
□ accélération d’un point
□ mouvements MRU et MRUA
1. Le temps : instant et durée
□ un instant noté correspond à une date précise.
□ chaque étude de mouvement est associé à une origine des instants noté 
Souvent   s
□ un instant ultérieur est noté avec  
S’il y a plusieurs instants ultérieurs, on utilise la notation 
Lors de l’étude du mouvement on peut noter ces instants sur un axe horizontal, chaque
instant est associé à chaque position.
□ une duréecorrespond à un intervalle de temps qui s’écoule entre deux instants :
□ l’unité du Système International est la seconde de symbole « s »
1 h = 3600 s 1 min = 60 s
ex : en août 2015 Usain Bolt a gagné le championat du monde du 100 m en moins de 10 s.
Entre le départ 0 s et l’arrivée 9,79 s il a parcouru une distance de 100 m pendant une
durée     9,79  0  9,79 s.
□ le chronométrage mesure une durée. Il peut s’effectué grâce à un chronomètre manuel, à
déclenchement électronique automatique, ou à partir d’une vidéo. Le choix de l’appareil
ainsi que l’expérimentateur ont des conséquences sur la précision de la mesure.
ex : au 100 m nage libre à Rome en 1960, les trois chronomètres des juges, déclenchés
manuellement, ont indiqués 3 durées différentes : 55,2 s , 55,1 s , et 55,0 s.
Depuis le chronométrage s’effectue automatiquement avec une précision au 1/10 000e de seconde.
Au labo la précision des chronomètres est de 1/100e de seconde.

2
Rémy Maire 2015 - 2016
2. Système et Référentiel
□ le système est l’objet mobile que l’on étudie.
Dans tous les problèmes il pourra être assimilé à un point.
□ le référentiel est un solide fixe par rapport à la Terre par rapport auquel on étudie le
mouvement. Exemples : un arbre, une route, les murs du labo…
□ le référentiel est équipé d’un repère d’espace : c’est un axe à une dimension noté ()
avec une origine (point ) et orienté dans le sens du mouvement.
□ la distance  parcourue correspond à la distance  :   
□ pour traiter un exercice il est recommandé de faire un dessin selon le modèle ci-dessus.
□ on se limite durant ce cours à la cinématique à une dimension.
La cinématique à une dimension permet de traiter tous les problèmes dans lesquels le
mouvement a lieu selon une ligne droite, qu'il s'agisse, par exemple, de voitures qui roulent
à vitesse constante, qui freinent ou qui accélèrent, ou encore la chute verticale d’un objet.
3. Trajectoire
□ la trajectoire d’un point est la courbe formée par l’ensemble des positions successives de
ce point au cours du temps.
□ dans tous les exercices et problèmes de ce cours la trajectoire sera un segment, un
segment de droite, ou une droite. On parle alors de trajectoire rectiligne.
4. Vitesse
Il est important de différencier les deux types de vitesse qui seront à calculer dans les
exercices et problème :
□ vitesse moyenne :    
 en m     
en s
en m/s   

3
Rémy Maire 2015 - 2016
ex : un tram parcours la distance de 500 m entre deux arrêts pendant une durée de 60 s.
Sa vitesse moyenne est :  500 / 60  8,3 m/s.
□ vitesse instantanée : c’est la vitesse d’un point à un instant précis.
Il s’agit de celle indiquée par les compteurs de vitesse ou les radars.
La vitesse instantanée est différente de la vitesse moyenne (sauf pour le MRU )
La formule    ne fonctionne pas ! (sauf pour le MRU )
ex : le tram accélère au démarrage, sa vitesse instantanée lue au compteur à 1 s est :
0,5 m /s  8,3 m/s
□ on précise toujours avec un indice la date à laquelle on calcule la vitesse instantanée
□ changement d’unité : la vitesse peut aussi être exprimée en km / h : 1,0 m/s  3,6 km/h
ex: la limitation de vitesse en ville est de 50 km/h soit  50/3,6  13,9 m/s
□ La vitesse est une grandeur physique toujours positive
5. Accélération
□ l’accélération est définie comme le quotient de la variation de vitesse  pendant la
durée  .
□ accélération :   
 en m/s
en s
en m/s2
□ l’accélération montre donc de combien la vitesse change (augmente ou diminue) pendant
1 seconde.
□ l’accélération est positive si la vitesse augmente   
□ l’accélération est négative si la vitesse diminue   
ex : le tram accélère de la vitesse 0,5 m /s à 9,0 m /s pendant une durée de 25 s.
  (9,0 0,5) / 25  0.34 m / s2. L’accélération est bien positive car le tram accélère.
ex : un scooter passe de la vitesse 5,5 m /s à 1,0 m /s pendant une durée de 3,1 s.
  (1,0  5,5) / 3,1  1,45 m / s2. L’accélération est bien négative car le scooter ralenti.

4
Rémy Maire 2015 - 2016
6. Mouvements
□ un mouvement d’un point donne des informations sur la trajectoire et la vitesse de ce
point.
□ dans tous les exercices et problèmes de ce cours le mouvement sera rectiligne.
□ deux types de mouvements rectilignes seront étudiés : MRU et MRUA.
7. MRU
□ MRU : Mouvement Rectiligne Uniforme.
□ la trajectoire est rectiligne et la vitesse est uniforme c'est-à-dire constante.
□ c’est la seule situation où la vitesse instantanée en n’importe quel point est égale à la
vitesse moyenne :  … 
□ les distances entre les points sont égales pendant des durées égales :
□ graphiques du MRU :
□ équation de la position du MRU :     
ex : avec une équation de mouvement     
on peut affirmer qu’il s’agit d’un MRU dont la vitesse est :   

5
Rémy Maire 2015 - 2016
8. MRUA
□ MRUA : Mouvement Rectiligne Uniformément Accéléré.
□ la trajectoire est rectiligne et la vitesse varie. L’accélération est constante.
□ si la vitesse augmente il s’agit d’une accélération.   
Les distances entre les points augmentent pendant des durées égales
□ si la vitesse diminue il s’agit d’une décélération ou ralentissement.   
Les distances entre les points diminuent pendant des durées égales
□ équation de la position :  
   en m en s en m/s2
ex : avec une équation de position    
on peut affirmer qu’il s’agit d’un MRUA dont l’accélération est :       
□ équation de la vitesse :      en s en m/s2
ex : avec une équation de la vitesse    
on peut affirmer qu’il s’agit d’un MRUA dont l’accélération est :   
□ graphiques du MRUA :