Application n°1

DAEU / Physique, Niveau 10 / EC1 (Mécanique)
Page 1/3
Exercices d'application directe du cours :
Application n°1 :
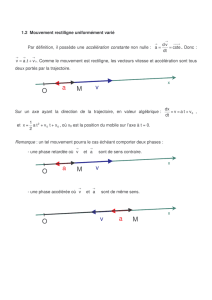
Le mouvement d'un mobile est donné par les équations horaires :
x(t) = 3t + 4 ; y(t) = 4t + 3.
Montrer que ce mouvement est rectiligne et uniforme.
A quelle date le mobile passera-t-il par le point x = 10 ? y = 15 ?
Application n°2 :
Un mobile animé d'un mouvement rectiligne et uniforme est à la date t = 1 s à
l'abscisse x = 8 m, et deux secondes plus tard en x = -4 m.
Quelle est l'équation horaire du mouvement ?
Quelle est la position du mobile à l'origine des dates ?
A quelle date le mobile est-il en x = 0 ?
Quelle est la distance parcourue en 5 secondes ?
Application n°3 :
Le mouvement d'un point mobile a pour équations horaires :
x = t² , y = 3 , z = 5 t2
Montrer que son mouvement est rectiligne et uniformément accéléré.
Donner l'expression de son accélération.
Application n°4 :
Une pierre est lancée verticalement vers le haut à partir d'une hauteur de 1 m
par rapport au sol. En prenant z = 0 au niveau du sol, son équation horaire est :
z = - 5 t2 + 4 t + 1.
1°) Donner l'expression de la vitesse .
2°) Calculer sa valeur aux dates t0 = 0s , t1 = 0,2s , t2 = 0,3 s et t3 = 0,5s.

DAEU / Physique, Niveau 10 / EC1 (Mécanique)
Page 2/3
3°) Montrer que cette vitesse s'annule. Calculer la date correspondante.
4°) Donner l'expression de son accélération.
5°) Montrer que son mouvement est rectiligne et uniformément accéléré.
Application n°5 :
Un automobiliste roulant à 90 km/h freine pour arrêter son véhicule. Le mou-
vement est alors uniformément varié et cesse au bout de 5 s. Calculer :
- l'accélération,
- la distance parcourue.
Application n°6 :
Une balle de golf, initialement au repos, est propulsée avec une vitesse de
valeur 30 m.s-1, faisant un angle de 45° avec l'horizontale.
Les équations horaires du mouvement sont respectivement
x = 30 2
2
t et z = - 5 t + 30 2
2
t
2
1) Retrouver à partir de la valeur de chacune des composantes la valeur ini-
tiale du vecteur vitesse.
2) Représenter la trajectoire de la balle.
3) Calculer sa vitesse au sommet de la trajectoire.
4) Calculer sa vitesse à son point de chute sur le sol horizontal.
Application n°7 :
Un manège démarre à la date t = 0. Dans cette phase, la vitesse d'un enfant
assis à 4 m du centre a pour expression v = 0,2 t
1) Déterminer les composantes du vecteur accélération à t1 = 10 s
2) A partir de cette date le mouvement est uniforme. Que devient l'accélération ?
3) Le manège s'arrête en 10 secondes, au cours desquelles la vitesse décroît régu-
lièrement.
Donner les expressions des composantes tangentielle et normale de
a
→
au
début du ralentissement.

DAEU / Physique, Niveau 10 / EC1 (Mécanique)
Page 3/3
Application n°8 :
Les deux aiguilles d'une horloge se déplacent d'un mouvement continu.
1) Déterminer l'équation horaire de l'extrémité de la grande aiguille qui mesure
15 cm. (On précisera la date choisie comme date origine.)
2) Même question pour la petite aiguille qui mesure 8 cm.
3) Déterminer l'accélération de l'extrémité de chaque aiguille. Préciser sa
direction.
Application n°9 ( généralisation) :
Le mouvement d'un point mobile a pour équation le long de sa trajectoire cir-
culaire: s(t) = 4t + 5
Calculer les composantes et la valeur de l'accélération pour t = 5s, sachant
que le rayon vaut R = 0,5m.
Même question si l'équation est : s(t) = 8t² - 6t + 10
Application n°10 :
Un disque de 25 cm de diamètre tourne à la vitesse constante de 45 tours par
minute.
- Quelle est sa vitesse angulaire ?
-Quelle est la vitesse linéaire d'un point du bord du disque ?
- Ce point a-t-il une accélération ? Si oui, donner sa direction et sa valeur. Si
non, justifier.