Fiche démonstration Pythagore Méthode chinoise 4e Sur cette

Fiche démonstration Pythagore Méthode chinoise 4e
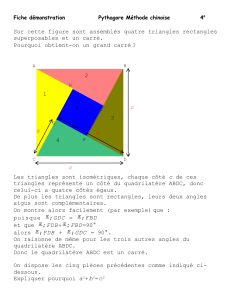
Sur cette figure sont assemblés quatre triangles rectangles
superposables et un carré.
Pourquoi obtient-on un grand carré ?
Les triangles sont isométriques, chaque côté c de ces
triangles représente un côté du quadrilatère ABDC, donc
celui-ci a quatre côtés égaux.
De plus les triangles sont rectangles, leurs deux angles
aigus sont complémentaires.
On montre alors facilement (par exemple) que :
puisque Æ;GDC = Æ;FBD
et que Æ;FDB+Æ;FBD=90°
alors Æ;FDB + Æ;GDC = 90°.
On raisonne de même pour les trois autres angles du
quadrilatère ABDC.
Donc le quadrilatère ABDC est un carré.
On dispose les cinq pièces précédentes comme indiqué ci-
dessous.
Expliquer pourquoi a2+b2=c2
A B
C D
E
G
H
F
c
c
b
a
1
2
3
4
5

A B
C D E
F'
G'H J
b
b
a
a
1
2
3
4
5
Cette démonstration du théorème de Pythagore est une
preuve chinoise qui date de la dynastie des Hans (200 av.
J.C., 200 ap. J.C.)
En 1968, dans son ouvrage the Pythagorean Proposition,
Elisha Scott a recensé 367 démonstrations différentes du
théorème de Pythagore.