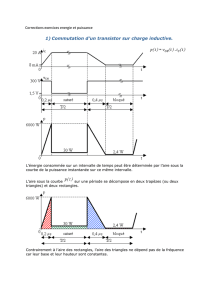
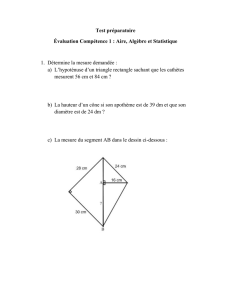
Intégration - Académie en ligne

1
Séquence 6 – MA01
Séquence 6
Sommaire
1. Pré-requis
2. Aire et intégrale d’une fonction continue et positive
sur un intervalle
3. Primitives
4. Primitives et intégrale d’une fonction continue sur un intervalle
5. Synthèse de la séquence
6. Exercices de synthèse
 Introduire une nouvelle notion : l’intégrale d’une fonction sur un intervalle
ab ;.
 Après une première approche géométrique, l’introduction de la notion de primitive
permet d’élargir la définition et les possibilités de calcul.
 Quelques exemples d’applications en Économie sont ensuite donnés.
Objectifs de la séquence
Intégration
© Cned - Académie en ligne

3
Séquence 6 – MA01
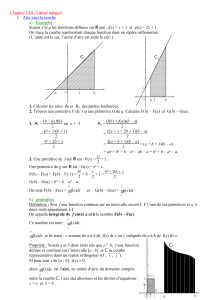
1Pré-requis
Aires
1. Aires usuelles
On considère des figures dans un plan où une unité de longueur a été choisie.
On sait calculer les aires déterminées par différentes figures géométriques :
 Aire d’un triangle : base hauteur×
2 ;
 Aire d’un rectangle : longueur largeur× ;
 Aire d’un trapèze : petite base + grande base hauteur
2
()
× ;
 Aire d’un disque : π×rayon2.
2. Propriétés des aires
 Additivité
Pour calculer l’aire de figures moins simples que les précédentes, on peut décom-
poser celles-ci en un certain nombre de figures dont on sait calculer l’aire. Par
exemple, pour calculer l’aire d’un polygone, on peut le décomposer en un certain
nombre de triangles. La somme des aires des triangles donne alors le résultat
souhaité. La propriété utilisée s’appelle l’additivité de l’aire, elle est énoncée dans
la propriété suivante.
On a l’habitude d’appeler « domaines » les ensembles de points du plan dont on
calcule les aires.
A
Vocabulaire :
© Cned - Académie en ligne

4
Séquence 6 – MA01
Propriété
Si 1 et 2 sont deux domaines du plan
dont l’intersection a une aire nulle alors
l’aire de 
12
∪ est égale à la somme
des aires de 1 et 2:
Aire 
12
∪
(
)
= Aire 1
(
)
+ Aire 2
(
)
.
Dans la figure ci-contre :
Aire ABCD Aire ABD Aire BCD
(
)
=
(
)
+
(
)
.
A
B
C
D
1
2
 Inclusion
Soit 1 et 2 deux domaines du plan tels
que
⊂
21
alors aire
()
≤
2
aire
.
1
()
 Translation, symétrie
Propriété Invariance par translation
Soit une translation
tv
 et deux domaines du plan 1
et 2 tels que 2 soit l’image de 1 par la trans-
lation tv
 (c’est-à-dire que tous les points du domaine
2 sont obtenus par translation de tous les points du
domaine 1 ). Alors les domaines 1 et 2 ont la
même aire :
aire 1
(
)
= aire 2
(
)
.
1
2
v
1
2
© Cned - Académie en ligne

5
Séquence 6 – MA01
Propriété Invariance par symétrie
Soit
s
 une symétrie axiale d’axe  et deux
domaines du plan 1 et 2 tels que 2 soit
l’image de 1 par la symétrie s
 (c’est-à-dire
que tous les points du domaine 2 sont obte-
nus par symétrie de tous les points du domaine
1 ). Alors les domaines 1 et 2 ont la même
aire : aire aire
12
(
)
=
(
)
.
1
2
3. Domaines, aires et mesures
On confond parfois un domaine (une surface) avec une aire, ou une aire avec une
de ses mesures.
On précise ici par un exemple la différence entre ces notions.
Un domaine est un ensemble de points du plan.
Des domaines qui sont des ensembles de points différents, sont des domaines dif-
férents, mais ces domaines peuvent avoir la même aire comme les trois domaines
ci-dessous qui ont chacun une aire égale à 12 carreaux.
Mesurer une aire, c’est lui associer un nombre en utilisant une aire de référence,
l’unité.
Prenons l’exemple d’une aire  de 1m2. On peut écrire l’égalité
==1m 10000 cm
22
 mais bien sûr les nombres 1 et 10000 ne sont pas égaux.
Le nombre 1 est la mesure de l’aire  en m2 et 10000 est la mesure de la même
aire  avec une autre unité, le cm2 .
© Cned - Académie en ligne

6
Séquence 6 – MA01
Dans cette séquence, les intégrales sont des nombres et ces nombres sont utilisés
pour mesurer des aires, l’unité étant souvent appelée « unité d’aire » ce que l’on
note u.a.
Il faut faire attention aux unités. Si l’unité d’aire est donnée par un repère où
l’unité est 2cm sur chaque axe, on aura 14u.a. cm2
=.
Il arrive que, quelquefois, on confonde une aire avec une de ses mesures.
Dérivation
Comme on le verra, les deux notions de dérivation et d’intégration sont très liées,
on rappelle donc ici les formules essentielles qui doivent être connues.
1. Fonctions usuelles
Expression de fx ()
f dérivable sur l’intervalle I
Expression de fx '( )
fx k () ,= k constante réelle
I =
fx '( ) =0
fx x ()=
I =
fx '( ) =1
fx x ()=1
I ==+∞
+
*;0 ou
][
==−∞
−
I *;0
fx x '( ) =− 1
2
fx x ()=
I ==+∞
+
*;0 fx x '( ) =1
2
fx x n
n
() ,=∈
∗
I =
fx nx
n
'( ) =−1
fx xxn
n
n
() ,== ∈
−∗
1
I ==+∞
+
*;0 ou
I ==−∞
−
* ;0
fx n
xnx
n
n
'( ) =− =−
+
−−
1
1
fx x ()=e I = fx fx x '( ) ( )==e
fx x () ln= I ==+∞
+
*;0
fx x '( ) =1
B
© Cned - Académie en ligne