TD 3 - Exercices sur le mouvement d`objets ponctuels - Marie

TD 3 - Exercices sur le mouvement d’objets ponctuels
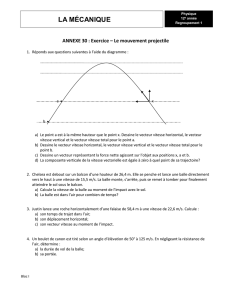
1. La figure 1 reporte l’acc´el´eration au cours du temps a(t) d’un (petit) chien chihuahua
alors qu’il poursuit un (gros) chien sheperd allemand, le mouvement ´etant enti`erement
r´ealis´e le long d’un axe unidimensionnel. Dans quelle(s) p´eriode(s) de temps le chien
chihuahua a-t-il un mouvement `a vitesse constante ?
Figure 1 –
2. En 1992, le record de vitesse de p´edalage `a bicyclette a ´et´e obtenu par Chris Huber.
Son record ´etait d’avoir parcouru 200 men 6.509 s. En 2001, ce record a ´et´e battu par
Sam Whittingham. Il a en effet battu le record de vitesse d´etenu par Sam Whittingham
de 19 km/h. Quel est donc le temps r´ealis´e par Sam Whittingham pour parcourir `a
bicyclette la distance de 200 m?
3. La position au cours du temps d’un objet se d´epla¸cant le long de l’axe des xsuit la
loi : x(t)=3t−4t2+t3, o`u xest en met ten s.
Trouvez la position de l’objet aux instants t= 1 s, 2 s, 3 s, 4 s. Quel est le d´eplacement
de l’objet entre t= 0 et t= 4 s?
Quelle est la loi de vitesse v(t) suivie par cet objet ? Quelle est la vitesse moyenne
entre t= 2 et t= 4 s?
4. Si la position d’une particule est donn´ee par x(t) = 20t−5t3o`u test en met ten s,
quand (si cela existe) la particule a-t-elle une vitesse nulle ? Quand l’acc´el´eration de
cette particule est-elle nulle ? Pour quels intervalles de temps cette particule peut-elle
avooir une acc´el´eration n´egative ? une acc´el´eration positive ?
5. Des gouttes de pluie tombent de nuages localis´es 1700 mau-dessus du sol. En consid´erant
que ces gouttes ne sont pas ralenties par la r´esistance de l’air, quelle est la vitesse de
1

ces gouttes lorsqu’elles atteignent le sol ? Est-il dangereux ou non de marcher sous la
pluie lorsqu’un orage a lieu ?
6. Un joueur de base-ball est sur le banc de touche et s’amuse et passe son temps `a
lancer la balle de base-ball verticalement en l’air. Au moment o`u on observe ce joueur
il lance la balle de base-ball verticalement le long de l’axe yavec une vitesse initiale
de 12 m/s.
1) Combien de temps faut-il `a la balle pour atteindre sa hauteur maximale au-dessus
de son point de lanc´ee initial ?
2) Quelle est la hauteur maximale atteinte par la balle au-dessus de son point de lanc´ee
initial ?
3) Quel temps faut-il `a la balle pour atteindre une hauteur de 5 m au-dessus de son
point de lanc´ee initial ?
7. Une mongolfi`ere se d´eplace verticalement du sol vers le ciel suivant l’axe des y`a la
vitesse de 12 m/s et se trouve `a la hauteur de 80 mlorsqu’un paquet est jet´e en dehors
de la nacelle. Quel temps faut-il au paquet pour atteindre le sol ? Avec quelle vitesse
ce paquet atteint-il le sol ?
8. Un lapin court `a travers un champ pour lequel un rep`ere `a 2-dimensions d’axes ortho-
norm´es (−→ i , −→ j) nous permet d’exprimer des vecteurs positions, vitesses et acc´el´erations
dans l’espace. Les coordonn´ees xet yde ce lapin au cours du temps sont :
x=−0.31t2+ 7.2t+ 28
y= 0.22t2−9.1t+ 30
A l’instant t= 15 s, quel est le vecteur position −→ rde ce lapin ? Donner 2 r´eponses :
1) une r´eponse en notation vecteur dans le rep`ere unitaire (−→ i , −→ j), 2) et une r´eponse
en notation amplitude/angle du vecteur.
Trouver le vecteur vitesse du lapin au mˆeme instant. De mˆeme, donnez deux fa¸cons
d’exprimer le vecteur vitesse.
Mˆemes questions pour le vecteur acc´el´eration `a l’instant t= 15 s.
9. Un ´el´ephant se d´epla¸cant dans l’espace `a 3-dimensions se trouve `a un instant taux
coordonn´ees d’espace suivantes : x=−5m,y= 8 m,z= 0 m. Donnez son vecteur
position −→ r, (a) en termes de composantes dans un rep`ere orthonorm´e (−→ i , −→ j , −→ k), et
2

en termes d’amplitude/angle par rapport `a la direction des x. Tracez le vecteur dans
ce rep`ere `a 3-dimensions.
10. La position d’une fourmi est donn´ee par le vecteur −→ rsuivant dans un rep`ere ortho-
norm´e (−→ i , −→ j , −→ k) : −→ r= 3.0t−→ i−4.0t2−→ j+ 2.0−→ k, avec ten set −→ ren m.
Donnez le vecteur vitesse −→ vde cette fourmi. Quel est −→ v`a l’instant t= 2.0s? Donnez
l’amplitude de −→ vet l’angle form´e par ce vecteur et l’axe des x.
Donnez le vecteur acc´el´eration −→ ade cette fourmi. Quel est −→ a`a l’instant t= 2.0s?
11. Une pierre est catapult´ee `a l’instant initial t= 0 avec une vitesse intiale d’amplitude
20 m/s avec un angle de +40◦par rapport `a un axe horizontal.
Quel est le mouvement de ce projectile, en distinguant le mouvement suivant l’axe
horizontal rep´er´e par le vecteur unitaire −→ iet le mouvement suivant l’axe vertical
rep´er´e par le vecteur unitaire −→ j, les deux vecteurs ´etant orthogonaux.
Quelles sont les composantes horizontale et verticale du vecteur d´eplacement de la
pierre par rapport `a son point de lancement `a l’instant t= 1.10 s?
R´epondre `a la mˆeme question pour l’instant t= 1.80 set t= 5.00 s.
12. On tire une balle `a partir d’un pistolet qui est localis´e `a 45 mau-dessus du sol, la balle
sort du pistolet avec la vitesse initiale de 250 m/s, le vecteur vitesse ´etant horizontal.
Donnez les ´equations du mouvement de ce projectile.
Pendant combien de temps la balle reste-t-elle en l’air ?
A quelle distance horizontale du point de tir initial la balle touche-t-elle le sol ?
Quelle est l’amplitude de la composante verticale de la vitesse lorsque la balle touche
le sol ?
13. Sur la figure 2, un bateau de pirate est positionn´e `a la distance R= 560 md’un fort
Figure 2 –
3

de d´efense `a l’entr´ee d’un port d’une ˆıle. Un canon de d´efense localis´e au niveau de la
mer tire des balles `a la vitesse initiale v0= 82 m/s.
Avec quel angle θ0par rapport `a la ligne horizontale doit-on tirer une balle de canon
afin que celle-ci atteigne le bateau ?
Quelle est la port´ee (=distance) maximale de ce canon, en d’autres termes quel est la
distance Rmaximale possible d’envoi d’une balle de canon ?
14. Comme illustr´e sur la figure 3 une pierre est jet´ee contre un mur de hauteur havec
une vitesse initiale de 42 m/s et un angle initial θ0= 60◦au-dessus de l’horizontale.
La pierre atteint le mur au point A, 5.50 sapr`es avoir ´et´e projet´ee.
Trouvez la hauteur hdu mur.
Trouvez la vitesse de la pierre au moment de l’impact en A.
Trouvez la hauteur maximale Hatteinte par la pierre durant son d´eplacement.
Figure 3 –
15. A quelle vitesse initiale le joueur de basketball repr´esent´e sur la figure 4 doit-il lancer le
ballon pour qu’elle rentre dans le panier ? On supposera que l’angle initial de lanc´e du
ballon de basket se fait avec l’angle θ0= 55◦au-dessus de l’horizontale. Les distances
not´ees sur le sch´ema sont d1= 0.5m,d2= 5 m,h1= 2 m,h2= 3 m.
Figure 4 –
4

Exercices suppl´ementaires d’entrainement
16. Une voiture se d´eplace en ligne droite sur une distance de 40 km `a la vitesse de
30 km/h. Elle continue ensuite suivant la mˆeme direction sur une distance de 40 km
`a la vitesse de 60 km/h.
1) Quelle est la vitesse moyenne de la voiture le long de ce chemin de 80 km ? (on
suppose que la voiture roule dans la direction +xde l’axe des x)
2) Faites un dessin de l’´evolution de la position xde la voiture en fonction du temps,
et expliquez comment trouver la vitesse moyenne graphiquement.
17. Sur la figure 5 on voit une situation typique dans laquelle un groupe de personnes es-
saye de s’enfuir par un couloir pour atteindre une porte qui leur permettrait d’´echapper
`a un feu (ils se d´eplacent de la gauche vers la droite). Le probl`eme est que la porte
est ferm´ee ! Chaque personne se d´eplace vers la porte `a la vitesse de 3.5 m/s, occupe
un espace d’´epaisseur grosso-modo de d= 0.25 m, et chaque personne est s´epar´ee de
la personne la pr´ec´edant et la suivant de la distance L= 1.75 m. L’arrangement des
personnes sur la figure 5 correspond `a l’instant initial t= 0 des mouvements que nous
consid´erons.
1) A quel taux moyen le bouchon constitu´e par ces personnes contre la porte ferm´ee
se forme-t-il ?
2) A quel instant tle bouchon atteint-il une ´epaisseur de 5 m?
Figure 5 –
18. Deux trains se d´epla¸cant `a une vitesse de 30 km/h roulent sur une voie unidimen-
sionnelle et l’un vers l’autre. Un oiseau se d´epla¸cant `a la vitesse de 60 km/h d´ecolle
de l’avant de l’un des trains lorsque les 2 trains sont s´epar´es de la distance de 60 km
et se dirige directement vers l’autre train. Lorsqu’il atteint l’autre train, l’oiseau fait
5