Intégrales. Primitives

CALCULS D'AIRES. INTEGRALES. PRIMITIVES
1°) Intégrale d'une fonction.
Soit f une fonction définie sur [a ; b] et C sa courbe représentative dans un repère
orthogonal (O ;
→
i ;
→
j).
Si I est le point tel que
→
OI =
→
i , J le point tel que
→
OJ = et K le point tel que OIKJ
est un rectangle, on appelle unité d'aire et on note u.a l'aire du rectangle OIKJ.
Prop 1 et déf 1: Si f est continue et positive sur [a ; b], on admet que le domaine E
situé sous la courbe (entre la courbe, l'axe des abscisses, les droites
d'équations x = a et x = b) admet une aire.
On appelle intégrale de a à b de la fonction f, l'aire, en unités d'aire, du domaine E.
On la note ⌡
⌠ab f (x) dx = A(E).
Remarque : E est l'ensemble des points M(x ; y) tels que 
 a
≤
x
≤
b
0
≤
y
≤
f (x)
⌡
⌠ab f (x) dx = ⌡ ⌠ab f (t) dt = ⌡ ⌠ab f (u) du = …..
Exemple A = ⌡
⌠25 (x + 1) d x.
la courbe est ici la droite d'équation y = x + 1.
A est l'aire du trapèze AA'B'B
donc A = (AA' + BB') x AB
2 = (3 + 6) x 3 2 = 13,5 u.a.
Déf 2 : Si f est continue et négative sur [a ; b], on appelle intégrale de a à b
de la fonction f, l'opposé de l'aire, en unités d'aire, du domaine E situé
entre la courbe et l'axe des abscisses.
On la note ⌡
⌠ab f (x) dx = – A(E).
Remarque : si f
≥
0, l'aire est comptée positivement
si f
≤
0, l'aire est comptée négativement.
on dit que l'intégrale est une aire algébrique.
Déf 3 : Si f est continue et de signe non constant sur [a ; b], on appelle
intégrale de a à b la somme des "aires algébriques" des domaines situés
entre la courbe et l'axe des abscisses.
ici ⌡
⌠ab f (x) dx = – E1 + E2 – E3 + E4.
Déf 4 : Si la fonction f est continue sur un intervalle I, pour tous réels a et b de I,
si a
≥
≥ b ⌡
⌠ab f (x) dx = – ⌡ ⌠b
a f (x) dx
si a = b ⌡
⌠ab f (x) dx = 0.
o
J
I
K
o
1
1
K
a b
A
A'
B
B
'
1
1
O
Cf
x
y
A
A'
B
B'
1
1
Ox
1 u.a.
ab1
1
O
Cf
x
1 u.a.
E1
E2
E3
E4

2°) Propriétés de l'intégrale .
a) Relation de Chasles.
prop 2 : Soit f une fonction continue sur un intervalle I, a, b, c trois réels de I
⌡
⌠ac f (x) dx + ⌡ ⌠cb f (x) dx = ⌡ ⌠ab f (x) dx
b) Linéarité.
Th 1: Soit f et g deux fonctions continues sur un intervalle I, a, b deux réels de I , k un nombre réel.
⌡
⌠ab [k.f (x)] dx = k ⌡ ⌠ab f (x) dx
⌡
⌠ab (f + g) (x) dx = ⌡ ⌠ab [f (x) + g(x)] dx = ⌡ ⌠ab f (x) dx + ⌡ ⌠ab g (x) dx
c)Positivité et ordre.
Th 2 : Soit f et g deux fonctions continues sur un intervalle [a, b] (a
≤
≤ b)
si f est positive sur [a ; b] alors ⌡
⌠ab f (x) dx
≥
≥ 0
si f est négative sur [a ; b] alors ⌡
⌠ab f (x) dx
≤
≤ 0
si f
≤
≤ g sur [a ; b] alors ⌡
⌠ab f (x) dx
≤
≤ ⌡
⌠ab g (x) dx
remarque: les réciproques sont fausses : si f n'est pas de signe constant, l'intégrale peut être positive ou négative suivant
les exemples.
d) Valeur moyenne d'une fonction.
Th 3 : Inégalité de la moyenne.
Si f est une fonction continue sur [a ; b] telle que pour tout x de [a ; b],
m
≤
≤ f (x)
≤
≤ M, alors
m (b – a)
≤
≤ ⌡
⌠ab f (x) dx
≤
≤ M (b – a)
dans le cas où f est positive sur [a ; b],
l'aire sous la courbe est comprise entre l'aire du rectangle ABCD et l'aire
du rectangle ABEF
Déf 5 : Si f est une fonction continue sur [a ; b], on appelle valeur moyenne
de f sur [a ; b] le réel µµ = 1
b – a ⌡
⌠ab f (x) dx
on a m
≤
≤ µµ
≤
≤ M
dans le cas où f est positive sur [a ; b],
l'aire sous la courbe est égale à l'aire du rectangle ABGH.
e) Aire comprise entre deux courbes.
Th 4 : Soit deux fonctions f et g continues sur [a ; b],avec f
≤
≤ g ; l'aire du
domaine compris entre les courbes, représentatives des deux fonctions et les
droites d'équations x = a et x = b est ⌡
⌠ab ( g–f ) (x) dx.
a b1
1
Ox
y
c
A B1
1
Ox
y
m
DC
M
FE
a bO x
y
A
B
1
1
O
x
y
m
D
C
M
F
E
µ
H
G

f ) Fonction paire, fonction impaire.
th 5 : Soit f une fonction définie et continue sur un intervalle [-a ; a], où a est un réel.
Si f est une fonction paire alors ⌡
⌠-a
a f (x) dx = 2 ⌡
⌠0a f (x) dx.
Si f est une fonction impaire alors ⌡
⌠-a
a f (x) dx = 0.
3°) Intégrales et primitives.
a) Primitive d'une fonction.
Déf 6 : Soit f une fonction continue sur un intervalle I. On appelle primitive de f sur I toute fonction F dérivable
sur I telle que F ' = f .
Prop 3 : Si f est une fonction continue sur un intervalle I et si a appartient à I, alors la fonction F définie sur I par
F (x) = ⌡
⌠ax f (t) dt est une primitive de f sur I.
Prop 4 : Toute fonction continue sur I admet une infinité de primitives sur I.
Si F est une primitive de f, alors l'ensemble des primitives de f sur I est l'ensemble des fonctions G telles que
G(x) = F(x) + k avec k réel.
ex : sur ]0 ; +
∞
[ , la fonction x
→
ln x est une primitive de la fonction x
→
1
x , les primitives de la fonction ln sont
donc les fonctions G telles que G(x) = ln x + k avec k réel.
Prop 5 : Si x0 est un réel donné dans I et y0 un réel quelconque.
Alors il existe une primitive et une seule F de f sur I telle que G(x0) = y0.
Th 6 : Si f est une fonction continue sur un intervalle I et si a appartient à I, alors la fonction F définie sur I par
F(x) = ⌡
⌠ax f (x) dx est l'unique primitive de f sur I s'annulant pour x = a. ( F(a) = 0).
b) Calcul d'une intégrale à l'aide d'une primitive.
Th 7 : Si f est une fonction continue sur un intervalle I et si a et b appartiennent à I, alors, pour toute primitive F
de f sur I, ⌡
⌠ab f (x) dx = F(b) – F(a).
ex : ⌡
⌠12 1
x dx = [ ln x] 2
1 = ln 2 – ln 1 = ln 2.
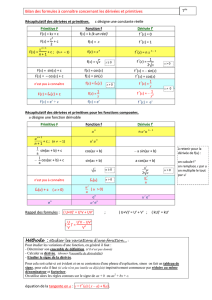
4°) Calculs de primitives.
a) Primitives des fonctions usuelles.
f (x)F (x)intervalle de validité
kk x + C IR
x n , n
∈
IN x n + 1
n + 1 + C IR
1
xln
x + C ] –
∞
; 0 [ou ]0 ; +
∞
[
1
x 2 = x - 2 – 1 x + C ] –
∞
; 0 [ou ]0 ; +
∞
[
1x = x –1/2 2 x + C ]0 ; +
∞
[
-
a a1
1
O
-a a1
1
O
la dérivée de x 3 est 3 x 3 – 1 = 3 x ²
la dérivée de 1
3 x 3 est 1 3 . 3 x ² = x ²
donc 1
3 x 3 est une primitive de x ² .
de même : 1
4 x 4 est une primitive de x 3 .
l'exposant augmente de 1 et on divise par le
nouvel exposant.

x n , n entier négatif
n
≠
-1 x n + 1
n + 1 + C ]-
∞
;0[ ou ]0 ; +
∞
[
x α , α
∈
IR – {-1} x α + 1
α + 1 + C ]0 ; +
∞
[
e xe x +C IR
cos xsin x + C IR
sin x- cos x + C IR
e a x a
≠
0 1
a e a x + CIR
b) Primitives des fonctions composées usuelles.
f (x)avec u dérivable sur I et … primitive
u n u' , n
∈
z, n
≠
-1 u ne s'annule pas sur I
quand n
≤
-2 u n + 1
n + 1 + C
u'
u ² u ne s'annule pas sur I – 1 u + C
u'
uu > 0 sur I 2 u + C
u'
u u ne s'annulant pas donc de
de signe constant sur I ln
u + C
u' e ue u + C
u' cos u sin u + C
u' sin u – cos u + C
u(a x + b) a
≠
0 U une primitive de u 1
a U(a x + b) + C
ex ⌡
⌠13 (3 x – 4 )5 dx = 1
3 
(3 x – 4) 6
6 3
1 = 1
3 ( 5 6 6 – (-1) 6 6 ) = 1 3 ( 15625 – 1 6 ) = 1 3 x 2604 = 868
c) Méthode d'intégration par parties.
Th 8 : Si u et v sont deux fonctions dérivables sur I telles que u' et v' soient continues sur I, alors pour tous réels
a et b de I : ⌡
⌠ab u(x) v'(x) dx = [u(x) v(x)] b
a – ⌡
⌠ab u'(x) v(x) dx
ex calculer ⌡
⌠01 (x + 1) e – 2 x dx
on ne connaît pas directement une primitive de (x + 1) e – 2x
on pose u(x) = x + 1 donc u'(x) = 1 on va dériver u car on va passer du degré 1 au degré 0 (une constante)
v '(x) = e – 2 x donc v(x) = e – 2 x
-2
donc ⌡
⌠01 (x + 1) e –2 x dx = 
(x + 1) e – 2 x
-2 1
0 – ⌡
⌠01 1 e – 2 x
-2 dx = 2 e - 2 -2 –1 e 0 -2 + 1 2 ⌡
⌠01 e – 2 xdx =
– e – 2 + 1
2 + 1 2 
e – 2 x
-2 1
0 = – e – 2 + 1
2 + 1 2 ( e - 2 -2 – e 0 -2 ) = – e – 2 + 1 2 – e – 2 4 + 1 4 = – 5 e – 2 4 + 3 4
ex calculer ⌡
⌠1e (x – 2 ) ln x dx
on pose u(x) = ln x donc u'(x) = 1
x. on ne connaît pas de primitive de la fonction ln, on va donc la dériver
v '(x) = (x – 2) donc v(x) = x ²
2 – 2 x
⌡
⌠1e (x – 2 ) ln x dx = 
ln x ( x ²
2 – 2 x) e
1 – ⌡
⌠1e 1
x ( x ² 2 – 2 x) d x = [ln e ( e ² 2 – 2e) – ln 1 ( 1 2 – 2)] – ⌡
⌠1e ( x
2 – 2) dx =
e ²
2 – 2e – 
1
2 x ² 2 – 2 x e
1 = e ²
2 – 2e – [ ( e ² 4 – 2 e) – ( 1 4 – 2)] = e ² 2 – 2e – e ² 4 + 2 e – 7 4 = e ² 4 – 7 4
.
attention la dérivée de sin x est cos x mais
une primitive de sin x est – cos x car
( - cos x )' = – (cos x)' = – (- sin x) = sin x
de même la dérivée de cos x est –sin x
mais une primitive de cos x est sin x car
( sin x )' = cos x

5°) Calcul de volumes.
Déf 7: unité de volume.
L'espace étant muni d'un repère orthogonal (O ;
→
→
i ;
→
→
j ;
→
→
k) , on appelle unité
de volume et on note u.v. ,le volume du parallélépipède OADBCEFG
tel que
→
→
OA =
→
→
i,
→
→
OB =
→
→
j,
→
→
OC =
→
→
k.
Th 9 (admis) :
L'espace étant muni d'un repère orthogonal (O ;
→
→
i ;
→
→
j ;
→
→
k) , soit a et b deux réels tels que a
≤
≤ b et S un solide
compris entre deux plans P(a) et P(b) parallèles d'équations respectives z = a et z = b.
Soit P(t) le plan perpendiculaire à l'axe (Oz) d'équation z = t, et S(t) l'aire de la section du solide S par le plan P(t).
Si la fonction t
→
→ S(t) est continue sur l'intervalle [a; b], alors le volume V du solide , en u.v. est donné par
V = ⌡
⌠ab S(t) dt.
Th 10 : L'espace étant muni d'un repère orthonormal (O ;
→
→
i ;
→
→
j ;
→
→
k) , soit a et b deux réels tels que a
≤
≤ b.
Soit f une fonction continue et positive sur [a; b], et C sa courbe représentative dans le repère (O ;
→
→
i ;
→
→
j ).
On note D le domaine limité par C, l'axe (O ;
→
→
i) et les droites d'équations x = a et x = b.
Alors le volume V du solide de révolution engendré par la rotation de D autour de l'axe (O ;
→
→
i) est
V = ππ ⌡
⌠ab ( f (t) )² dt u.v.
6°) Cinématique.
Prop 6 : Soit un mobile M en mouvement sur une droite D munie d'un repère (O ;
→
→
i).
Soit les fonctions X : t
→
→ X (t) et V t
→
→ X ' (t) = dX(t)
dt qui représentent respectivement l'équation du
mouvement et la vitesse du mobile M.
La vitesse moyenne du mobile entre les instants t1 et t2 (t1 < t2 ) est le réel: 1
t2 – t1 ⌡
⌠t1
t2 V(t) dt.
ex : un mobile se déplace sur une droite, sa vitesse est donnée pour t
≥
0 par V(t) = -5 t + 10.
Calculer sa vitesse moyenne entre les instants 1 et 5.
v1-5 = 1
5 – 1 ⌡
⌠15 (- 5 t + 10) dt = 1
4 
– 5
2 t ² + 10 t 5
1 = 1
4 [ ( - 125 2 + 50) – (- 5 2 + 10)] = – 5
on peut vérifier : sa position est donnée par une primitive de V : X = - 5
2 t ² + 10 t.
X(1) = 15
2 et X(5) = - 25 2 ; l'écart des positions est -40 2 = - 20 pour un écart de temps de 4 s; la vitesse moyenne est bien - 5
RESTITUTION ORGANISEE DE CONNAISSANCES
Pré-requis : " Soit f et g deux fonctions définies et continues sur un intervalle I de IR.
Soit a et b deux réels appartenant à I tels que a
≤
b.
Si pour tout x de [a; b], f (x)
≥
0 , alors ⌡
⌠ab f (x) d x
≥
0. "
1. questions de cours.
a) Soit f et g deux fonctions définies et continues sur un intervalle I de IR.
Soit a et b deux réels appartenant à I tels que a
≤
b.
Démontrer les propriétés suivantes :
(P1) :
∀
x
∈
[a ; b], f (x)
≤
g (x) ⇒ ⌡
⌠ab f (x) d x
≤
⌡
⌠ab g (x) d x.
(P2) : si m et M sont deux réels tels que pour tout x de [a ; b] , m
≤
f (x)
≤
M ,
alors m (b – a)
≤
⌡
⌠ab f (x) d x
≤
M (b – a) .
b) Soit f une fonction définie et continue sur un intervalle I de IR, soit a et b deux réels appartenant à I.
Démontrer la propriété suivante :
(P3) : si M est un réel strictement positif tel que pour tout x de I f (x)
≤
M , alors ⌡
⌠ab f (x) d x
≤
M b – a .
2. Application : Démontrer que : pour tout réel x et tout réel y, sin(x) – sin(y)
≤
x – y .
Réponse : on va utiliser la propriété (P3) avec f (t) = cos t.
⌡
⌠yx cos t dt = [ ]
sin t x
y = sin x – sin y.
pour tout réel t, – 1
≤
cos t
≤
1 donc cos t
≤
1.
Donc d'après la propriété (P3) ⌡
⌠yx cos t dt
≤
1 x – y donc sin x – sin y
≤
x – y .
x
y
o
A
B
C
D
EF
G
O