30BU03SV Outils pour Biologistes 2 TD 6 : surpression, impédance

30BU03SV Outils pour Biologistes 2
TD 6 : surpression, impédance, application à l’oreille
Exercices encadrés
Exercice 1 : Relation déplacement-intensité-
surpression
On considère une onde sonore, plane, progressive,
sinusoïdale, se propageant dans un milieu. Le
déplacement local des molécules du milieu s’écrit
sous la forme :
𝑢𝑥,𝑡=𝑢!sin(
2𝜋
𝜆(𝑥−𝑐𝑡))
où u0 est l’amplitude, λ est la longueur d’onde et c la
célérité de l’onde.

1. Rappeler la relation liant la célérité de l’onde c
avec λ et f (la fréquence de l’onde).
2. Calculer la vitesse des molécules 𝑣𝑥,𝑡 et
exprimer son amplitude 𝑣! en fonction de 𝑢! et f.
3. On appelle 𝑍=𝜌𝑐 l’impédance acoustique du
milieu, où ρ est la masse volumique du milieu. Quelle
est la dimension de Z ? En déduire ses unités.
4. Calculer l’impédance de l’eau en sachant que la
célérité du son dans l’eau est ceau = 1500 m.s-1 (vous
devez connaître la masse volumique de l’eau !).
5. Par analyse dimensionnelle, exprimer l’intensité
de l’onde en fonction de l’impédance Z et de
l’amplitude de la vitesse des particules 𝑣! à un facteur
numérique près.
L’intensité sonore s’exprime en fait de la façon
suivante :
𝐼=
1
2
𝑍𝑣!
!

La surpression 𝑝(𝑥,𝑡) créée par le déplacement des
molécules est proportionnelle à la vitesse de celles-
ci :
𝑝𝑥,𝑡=𝑍𝑣(𝑥,𝑡)
6. Exprimer l’intensité sonore I en fonction de 𝑍 et de
𝑝! amplitude de la surpression.
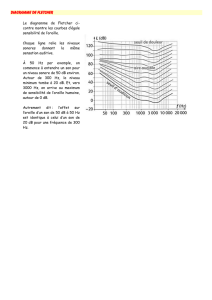
7. À température ambiante, Zair = 415 kg.m-2.s-1.
L’amplitude de surpression maximale supportable par
l’oreille humaine est d’environ 28 Pa. À quelle
intensité sonore cela correspond-il ? Quel est le
niveau sonore associé ?
8. Quelle est la vitesse de déplacement des
molécules d’air 𝑣!? A quelle amplitude 𝑢! du
déplacement des molécules cela correspond-il, à une
fréquence de 5 kHz ?
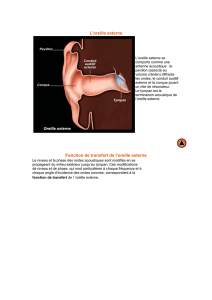
9. L’aire du tympan est environ 0,8 cm2. Quelle est la
force exercée sur le tympan lors du passage de cette
onde (ne pas oublier de convertir les cm2 !) ?

Exercice 2 : Réflexion/réfraction d’une onde
sonore
Lorsqu'une onde sonore traverse une interface entre
deux milieux de masse volumique et avec des
célérités différentes, l'onde va être partiellement
transmise et réfléchie.
1. Le coefficient de réflexion en intensité s’exprime en
fonction des impédances acoustiques des deux
milieux 𝑅=!!
!!
=(!!!!!)!
(!!!!!)!. En utilisant la conservation
de l’énergie, en déduire l'expression du coefficient de
transmission en intensité 𝑇=!!
!!
.
2. On considère une onde sonore se propageant à
l'interface entre deux milieux.
Trouver une expression approchée de T et de R dans
les trois cas suivants:
- 𝑍!≈𝑍!
- 𝑍!≫𝑍!
- 𝑍!≫𝑍!

Calculer numériquement T et R dans le cas d’une
interface entre l’eau et l’air.
3. Conclure sur la nécessité d'une adaptation
d'impédance si on veut qu’une onde soit transmise
sans trop de pertes au passage air-eau ou eau-air.
4. Expliquer pourquoi lors d'une échographie, un gel
est placé entre le transducteur (qui émet et reçoit
l'onde ultrasonore) et la peau du patient.
Exercices en autonomie
Exercice 3 : Comparaison air/eau
1. Si les amplitudes de surpression sont les mêmes
pour deux ondes sonores se propageant l’une dans
l’air et l’autre dans l’eau, quel est le rapport des
intensités de ces deux ondes ?
2. Si deux sons ont la même intensité dans l’air et
dans l’eau, quel est le rapport des surpressions
associées ?