Modélisation d`une photopile bifaciale au silicium : méthodes de

'"
UNIVERSITE CHEIKH ANTA DIOP DE DAKAR'
*********
FACULTE DES SCIENCES ET TECHNIQUES - DEPARTEMENT DE PHYSIQUE
*****
1
LABORATOIRE DES SEMI-,CONDUCTEURS ET D'ENERGIE SOLAIRE
THESI:;:,DE TROISIEME CYCLE
présentée par
M. Emmanuel NANEMA
Maître ès Sciences
'"
pour obtenir fe grade de DOCTEUR
Ir--'-'-"""=;=~~=';==--===-==-'
= = ---..
=-=-----==-..:===='='=1
Il
IVIODELISATION D'UNE PHOTOPILE BIFACIALE AU SILICIUM:
Il
METHODES DE DETERMINATION DES PARAMETRES DE
,1
RECOMBINAISON
1
1
_·.==.=,dJ
~'..::::l~~~.~'~=:,:",,"-=-"":._
. Soutenue publiquement le.~ 1 Octobre 1996 devant le jury composé de:
Président:
M, M. Mansour KANE
Professeur
Membres:
MM. Amadou Lamine N'DIAYE
Chargé d'enseignements
Boubacar IŒITA '
Chargé d'enseignements
Mamadou ADJ
Maître-Assistant
,
,
Grégoire SISSÇ)1(O
.,
Maître de Conférences
Ce travail a été effectué au Laboratoire des Semi-conducteurs et d'Energie Solaire (
Faculté des Sciences et Techniques ) et, au Laboratoire d'Energétique Appliquée ( Ecole
Supérieure Polytechnique) de l'Université Cheikh Anta DIOP de Dakar sous la direction de
Monsieur Grégoire SISSOKO.
Mes remerciements vont particulièrement à Monsieur le Professeur Mamadou Mansour
KANE, Chef du Département de Physique et Directeur du C. E. R. E. R. pour l'honneur qu'il
me fait en acceptant de présider mon jury.
Je remercie aussi Monsieur Amadou Lamine N'DIAYE, Chargé d'enseignement au
Département de Physique, pour avoir accepté de participer au jury.
Mes rçmerçLements vont également à Monsieur Boubacar .KEITA, Ch~rgé d'enseignement au
Département de Physique, poùr ses êncouragements, ses~n~eil~ tout au loog de ces années de
.
travail et sa disponibilité à participer à mon jury.
Que Monsieur Mamadou ADJ trouve ici ma profonde gratitude pour la disponibilité dont il fait
preuve en acceptant de participer à ce jury. Je vous suis reconnaissant pour avo"ir mis à ma
disposition tout le matériel informatique dont j'en avais besoin et sans lequel ce travail ne
pourrait être réalisé.
Qu'il me soit permis de remercier M. François ZOUGMORE, Maître de Conférence et Chef du
Département de Physique de l'Université de OUAGADOUGOU pour ses conseils et l'intérêt
qu'il a porté à ce travail.
Je voudrais également transmettre mes sincères remerciements à M. Mody DIARRA pour tous
les encouragements qu'il n'a cessé de me prodiguer pendant tout mon séjour dans le
département.
Je remercie enfin M. Grégoire SISSOKO pour ses constants efforts pour la réalisation de ce
travail. Qu'il y trouve toute ma profonde reconnaissance.
/~--~~~:0~
«;''-'0
Q ."
'/.
(.
,
~
.
REMERCIEMENTS
Mes remerciements vont particulièrement à Monsieur Managa Bamba SANKARA à
l'ASECNA (DAKAR) à qui je ne saurais trouver les mots justes pour lui témoigner ma
profonde reconnaissance pour l'aide morale et matérielle qu'il m'a apportée durant mon sejour à
DAKAR. Puisse le TOUT PUISSANT le lui rendre au centuple.
Je remercie tout particulièrement mes frères et soeurs (OUAGADOUGOU), la famille
BADINI (OUAGADOUGOU), les familles OUEDRAOGO et TAGNAN à l'ASECNA
(DAKAR), TRAORE, COMPAORE et SAWADOGO à la BCEAO (DAKAR) pour leur
soutient durant ces années de travail. Que chacun trouve dans ce travail le produit de ses
efforts à mon égard.
Je voudrais remercier également mon ami Fousseni TRAORE à OUAGADOUGOU pour son
soutient moral pendant les moments difficiles.
Je remercie tous mes compagnons d'équipe avec qui j'ai partagé les bons et les durs
moments de travail, les étudiants Burkinabé à Dakar, et plus particulièrement Mademoiselle
Olga COLY et sa famille grâce à qui mon séjour dans leur pays a été des plus agréables.
Je ne saurais trouver les mots convenables pour exprimer ma profonde reco'nnaissance
à Monsieur Grégoire SISSOKO et sa famille pour l'assistance aussi bien morale que matérielle
qu'ils m'ont apportées pour l'élaboration de ce travail. Ses bienfaits ne seront jamais oubliés.
Enfin, à toi ma compagne Blandine et à notre fille Eve, trouvez dans ce travail
l'expression de ma profonde reconnaissance pour ces longues années de privation et d'attente
que vous avez endurées.
TABLE DES MATIERES
.
1
. ............... 3
INTRODUCTION
BIBLIOGRAPHIE
.
CHAPITRE 1
ETUDE DE LA BASE D'UNE PHOTOPILE EN REGIME STATIQ{JE ECLAIREE
PAR SON EMETTEUR
. INTRODUCTION
:-:;
~
; -:- :
,:
l D~scriptioD d'une photopile _
II Etude de la densité des porteurs génères dans la base de la photopile
Il- 1 Résolution de l'équation de continuité
B-2 Etude de la densité des porteurs de charge
III Etude du courant dans la base de la photopile
aO) Photocourant en fonction de SFn
bO) Photocourant en fonction de SB.
IV Etude de laphototension
aO) Phototension en fonction de SFn
bO) Phototension en fonction de SB
V Etude en modélisation de la Caractéristique courant-tension dans la base
VI Le courant de diode
VII Puissance electrique délivrée par la base de la photopile
VIII Résistance de charge de la photopile
IX Etude de la capacité de l'élargissement de la zone de charge d'espace
CONCLUSION
BIBLIOGRAPHIE
, :
,
'5
5
6
7
8
12
13
17
22
23
24
25
26
28
31
33
35
36
CHAPITRE II
ETUDE DE L'EMETTEUR D'UNE PHOTOPILE EN REGIME STATIQUE
INTRODUCTION
1 Etude de la densité des trous dans l'emetteur..
1-1 -Rés.olution de l'équation de continuité
II-2 Etude de la densité des porteurs
II Etude du p'hotocourant des trous
III Etude de la phototension
. IV etude en modélisation de la Caractéristique courant-tension de l'émetteur de la
:
photopile
;
V Le courant
de
diode
:
.
.
'. VI Puissance délivrée par l'émetteur
:
:
:.....................
VII i"a résistance de charge de l'émetteur
VIII Etude dela capaCité de l'élargissement de la zone de charge d'espace
39
39
39
41'
43
45
46
47
49
51
52
CONCLUSION
54
55
BIBLIOGRAPHIE
CHAPITRE
In
·ETUDE EN REGIME STATIQUE D'UNE PHOTOPILE ECLAIREE PAR SA FACE
ARRIERE
INTRODUCTION
1 Etude ·de la densité des porteurs dans la base
II-l Résolution de l'équation de continuité
II:-2 Etude. de la densité des porteurs
_
_
Tl Etude du courant dan~ la base
aO) Photocourant en fonction de SFn
bO) Photocourant en fonction de SB.
III .Etude de la phototension
IV Caractéristiques courant-tension de la photopile
V Etude du courant de diode ou courant d'obscurité
VI Puissance delivrée par la base de la photopile
VII Résistance de charge de la photopile
IIX Etude de la capacité de l'élargissement de la zone de charge d'espace
CONCLUSION
:" - ; ,:
56
56
57
57
59
59
64
67
70
70
72
74
75
76
BIBLIOGRAPHIE
78
CHAPITRE IV
ETUDE DE LA CONTRIBUTION DE L'EMETTEUR ET DE LA BASE POUR UNE
PHOTOPILE BIFACIALE FONCTIONNANT EN REGIME STATIQUE
INTRODUCTION
1 Etude de la densité des porteurs....
II Etude du photocourant.
III Etude de la tension..
IV Caractéristiques courant-tension de la photopile éclairée par les deux faces
V Etude du courant de diode..........
,
VI Etude de la puissance délivrée par la photopile
VII Etude de la résistance de charge
:
IIX Etude de la capacité de j'élargissement de la zone de charge d'espace
CONCLUSiON
BIBLIOGRAPHIE
'"
.-
79
79
82
85
87
; 87
89
91
92
93
95
CHAPITRE V
METHODES DE DETERMINA~flONEN REGIME STATIQUE D,[S PARAMETRES
ELECTRONIQUES ET ELECTRIQUES D'UNEl~HOtÔPILE
INTRODUCTION
1 TECHNIQUE DE DETERMINATiON DES PARAMETRES ELECTRONIQUES
1°) Détermination de la longueur de diffusion L et de la vitesse de
recombinaison SB des porteurs dans la base de la photopile
2°) Discussions
_
11 TECHNIQUE DE DETERMINATION DES PARAMETRES ELECTRIQUES
1°) Détermination de la vitesse de recombinaison SFOn introduites par les états
__ _
_
d'interface
:
2°) Détermination de la résistance shunt Rsho et de la capacité Co de
_...........
l'élargissement de la zone de charge d'espace
1II APPLICATION DE LA TECHNIQUE DE DETERMINATION DES
. PARAMETRES A UNE PHOTOPILE ECLAIREE PAR LA FACE ARRIERE
CONCLUSION
BIBLIOGRApHIE
_
CONCLUSION ET PERSPECTIVES
96
96
96
97
99
99
lOO
101
]02
]04
106
INTRODUCTiON
L'intérêt de la conversion photovoltaïque est la production d'énergie. L'amélioration des
perfonnancesdes photopiles (qui constituent les éléments importants de cette conversion) est
un souci majeur vers lequel s'orientent les recherches actuelles. A cet effet, les photopiles ont
connu de nombreuses évolutions dans leurs structures, depuis les photopiles conventionnelles
jusqu'aux photopiles bifaciales pouvant être éclairées par les deux faces. Le but de ces
innovations est de produire des rendements meilleurs.
L'amélioration des performances des photopiles passe également par le contrôle de leur qualité
au cours des différentes phases de fabrication.
Divers proces~us de recombinaiso~s des porteurs rriinoritâires de charges en 'ëxëès généré<:i'
dans la phOtopile sous -excitation optique 'ou électrique limitent ses performances. Ce Sont
essentiellement les recombinaisons en volume ( recombinaisons Shockley-Read-Hall [1],
recombinaisons Auger [2], les recombinaisons radiatives ), et les recombinaisons en surface
(liées aux imperfections du réseau cristallin).
L'action de ces recombinaisons sur les paramètres électroniques ( durée de vie
't,
longueur de
diffusion L, vitesses de recombinaison SF à la jonction et SB sur la face arrière de la base )
influence la qualité de la photopile.
Il devient alors important d'élaborer des méthodes de caractérisation de ces paramètres afin de
les contrôler lors de la fabrication de la photopile.
Les techniques de caractérisation se divisent en deux groupes qui sont les techniques en régime
statique [3-10] et les techniques en régime dynamique [11-20].
Dans notre travail, nous nous proposons d'effectuer une étude en modélisation d'une photopile
éclairée par une lumière multispectrale sur les deux faces.
Dans le Chapitre l, nous étudions la base de la photopile pour un éclairement arrivant sur
l'émetteur. Nous extrairons ses paramètres macroscopiques ( courant, tension, puissance,
résistance de charge et capacité de l'élargissement de la jonction ). Nous étudierons également
l'effet des phénomènes de recombinaisons aux interfaces sur la qualité de la photopile.
Dans le chapitre Il, nous étudions l'émetteur de la photopile dans les conditions d'éclairement
du chapitre 1. L'effet des phénomènes d'interface sur la qualité de la photopile sera 'égaleme'iÜ -.-..
examiné
Le Chapitre III est une étude de la base de la photopile lorsque l'éclairement est effectué par la
face arrière. L'effet des recombinaisons aux interfaces sur la qualité de la photopile sera encore
examiné.
Le Chapitre IV est consacré à une étude comparative de la contribution de chaque
compartiment de .la photopile dans la production du courant. 11 situe l'im'portance de chacun
d'eux' dans le fonctionnement de la photopile.
2
Enfin, dans le chapitre V, nous apportons notre contribution en proposant de nouvelles
techniques de détennination des paramètres électriques et électroniques des photopiles
fonctionnant en régime statique.
..,
-'
BIBLIOGRAPHIE
[ 1]: S. M. SZE
Physics of Semiconductor Deviees, 2° Ed. Wiley lnterscience, New-York (u. S. A. ), p. 145
(1981 )
[2]: R. A. SINTON and P. M. SWANSON
"An Optimisation Study of Si Point Contact Concentration" 15th I.E.E.E. Photov. Spect.
Conf. (u. S. A.), pp. 1207-1208 (1987).
[3]: P. VERL1NDEN and VAN pE WIELE
Solid State EleetT. Vol 26, n-o II, pp. 1089-94 (1983)
[4]: M. SARITAS and H. D. MckeU
1. Appl. Phys. 63, (9), pp. 4561-67 (1988).
[5]: G. C. IAIN S. N. SINGH
SolaT Cells 8 (1983)
[6]: F. BERZ and H. K. KUNTEN
Solid State Electr. Vol 19, pA37 (1976)
[7]: A. JAKUBOWICZ
Solid State Electr. Vol 23, pp.635-39 (1980)
[8]: A. ROMANOWSKY and D. B. WlTTRY
1. Appl. Phys. 60 (8), 5 pp. '2910-13 (1986).
[9]: F. N. GONZALEZ and A. NEUGROSCHELL
J.E.E.E. Trans Elect. D. Vol. ED. 31 ppA13-16 (1984)
[10]: A. NEUGROSCHELL, P. 1. CHEN, S. C. PAO and F. A. LINDHOLM
I.E.E.E. Trans Elect. D. Vol. ED. 25 p485 (1978)
[II]: A. NEUGROSCHELL, P. J. CHEN, S. C. PAO and F. A. LINDHOLM
Pme. 13 th Photov. Sp. Conf. 70 (1978)
4
[12]: 1. GAYE, A. CORREA, A. L. NDIAYE, E. NANEMA, A. B. B. BA, M. ADJ, G.
SISSOKO, W. R. E. C. IV, 15-21 June, Denver, Colorado, (U.S.A.), pp. 1598, (1996)
[13]: A. CORREA, 1. GAYE, B. BA, L. NDIAYE and G. SISSOKO
Renewable Energy, Vol. 5, part l, pp. 166-168 Pergamon 1994
[14]: Y. L. B. BOCANDE, A. CORREA, 1. GAYE, M. L. SOW and G. SISSOKO
Renewable Energy, Vol. 5, part III, pp. 1698-1700 Pergamon' 1994
-
[15]:
-
9. SISSOKO, s. SIVOTHTHAMAN, M. RODOr; P. M1AL~'
>
fi th. European Photovoltaic Solar Energy Conference and Exhibiti'on, Poster 1 H, 12-16 Oct.
Montreux Switzerland, pp. 352-354 (1992).
[16]: M. MUNSK, G. MULLER, R. SCMlDTAND and H. WETZEL
Appt Phys. A, 46 pp. 77-85 (1988).
[17]: P. MIALHE, G. SISSOKO, F. PELANCHON, 1. M. SALAGNON
1. Phys,IIL France 2, pp. 2317-2331
[18]: P. MIAUIE, F. PELANCHON, G. SISSOKO, M. KANE
Solar World Congress, Denver (U.S.A.)17-24 August, pp. 407-412 (1991).
[19]: F. PELANCHON, G. SISSOKO, M. KANE, P. MIALHE
Modelling Simulation and Control A, AMSE Vol. 36, pp. 51-63 (1991)
[20]: P. MIALHE, G. SISSOKO,
1. Phys. D. 20 p. 762 (1987)
M. KANE
5
CHAPITRE 1
ETUDE DELA BASE D'UNE PHOTOPILE EN REGIME STATIQUE ECLArREE
PAR SON EMETTEUR
INTRODUCTION
Dans ce chapitre, nous étudions le fonctionnement en régime statique de la base d'une
photopile éclairée à l'aide de la lumière blanche par l'émetteur.
Nous déterminons les paramètres macroscopiques ( courant, tension, puissance éiectrique,
résist<mce, et capacité )·de1a ba'se:'
L'étude des recombinaisons des porteurs de charge' aux interfaces sera également
effectuée afin de déterminer l'influence de ces recombinaisons sur la puissance électrique de la
base de la photopile.
. 1 DESCRIPTION D'UNE PHOTOPILE
Une photopile au silicium comprend généralement deux zones:
-La première zone est appelée émetteur et elle est de très faible épaisseur (environ 1 ~m),
-La deuxième zone est appelée base et est d'épaisseur plus importante (environ 300
~m).
Par ailleurs, certaines cellules disposent d'une zone "surdopée" sur la face arrière de la
base dont la nature du dopage est la même que celle de la base: ce sont des photopiles à champ
arrière ou encore photopile Back Surface Field (B.S.F.) [1-1 .. 11].
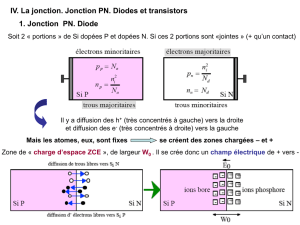
La figure (1-1) représente la structure simplifiée d'une photopile à une dimension dans le sens
de la p'rofondeur de la base:
Emetteur
Zone arrière
J,
J
n
x=-dEx=O
Base de type p
p+
x=Hx=W
Figure (1-1): Schéma simplifié d'une photopile
6
Généralement, l'émetteur est d~ type n et il fortement "dopé" par des atomes de
phosphore (environ 10 20 at/cm 3 ). La base quant à elle est de type p en général et elle est plus
faiblement "dopée" par des atomes de bore (environ 10] 7 at/cm 3 ).
Cependant, la jonction entre l'émetteur et la base est une troisième région appelée zone
de charge d'espace dont l'épaisseur sera négligée dans notre étude.
Sous l'effet d'une excitation ( optique ou électrique ) des porteurs de charge sont
générés dans la base. Nous étudions dans le paragraphe (II) la densité des porteurs de charge
générés dans la base de la photopile sous illumination.
~ Il ETUJ)E DE ·LA· DE'NSITE DES PORTEURS GENERES OANS LA BASE DE LA
PHOTOPILE
Les porteurs minoritaires de charge générés dans la base de la photopile (base dopée de
type p) sous l'effet de l'éclairement en lumière blanche sont des électrons de charge -q,
La densité de ces porteurs qui prend naissance dans la base obéit à l'équation de continuité qui
traduit la conservation des charges.
En tenant compte des phénomènes de génération, de recombinaison, de diffusion et de
conduction dans la cellule photovoltaïque, l'équation de continuité des porteurs qui sont
générés dans la base de la photopile en fonctionnement en régime statique est:
n (x)-n o
p
p
--'--------'- =-G(x)
-L2
n
D
(1-1 )
n
Dans cette équation:
n (x) désigne la densité des électrons générés dans la base de la photopile sous l'effet
p
de l'éclairement,
f1n désigne la mobilité des électrons,
D n désigne le coefficient de diffusion des électrons générés dans la base,
Ln désigne la longueur de diffusion des électrons dans la base,
nO est la concen-tration des électrons dans la base de la photopile à l'équilibre
p
thermodynamique,
G(x) désigne le taux de génération en lumière blanche des porteurs en fonction de la
profondeur de la base,
Nous écrirons G(x) sous la forme [1-12]:
.
7
3
-b.x
G(x) = L: a.e )
.
1)
1=
(1-2)
dans laquelle les tennes ai et bi tiennent compte des valeurs tabulées du rayonnement solaire et
de la dépendance du coefficient d'absorption du silicium avec la longueur d'onde [1-13].
U-l Résolution de l'équation de continuité
Posons:
-
Ô
2
=[ ~ nE.J + ~ 0 = ~ nE
o
L2 '
n
et y
20'
n
n
= .Ji
2
L'équation (1-1) devient:
G(x)
=---
on
(1-3)
L'équation (1-3) est une équation différentielle du second ordre dont la solution générale se
présente sous la fonne suivante:
n (x) - nO = e-...,r:l. x ( c ey '
p
p
1
X
3 K.e - b.) x
+ c e-Y. x) + L:
i=l
2
)
(1-4)
ou
a.
K. = 1
D
n
r~
b 1
\
)
20 . b.
1
___1
J2
J
-n
Nous détenninons les constantes c) et c 2 à l'aide des conditions aux limites suivantes:
1°)_ A la jonction:
(1-5)
8
an
(x)
p
ax
SF
1
x=O
= _n. n
D
n
p
(0)
(1-6)
SF n est la vitesse de recombinaison des électrons à la jonction. C'est un paramètre
phénoménologique. Il a deux composantes dont l'une est liée aux états d'interface et l'autre est
"gouvernée" par la charge externe qui fixe le point de fonctionnement de la photopile ( court
circuit, circuit ouvert ou point de fonctionnement intermédiaire) [1-14].
SF :::. SFO +SF
n
n
(1-7)
1
2°)-Sur la face arrière:
(1-8)
SB est la vitesse de recombinaison à la face arrière des électrons. Pour les photopiles
conventionnelles, la valeur de SB est élevée tandis que pour les photopiles B.S.F., cette valeur
est faible [1-13].
11-2 Etude de la densité des porteurs de charge
A l'aide de l'équation (1-4) munie de ses conditions aux limites, nous faisons une étude
en modélisation de la densité des porteurs générés dans la base pour différentes photopiles
caractérisées par leur champ cristallin sous illumination 1 AM ( la puissance incidente
correspondante est de 925 Watts/cm 2 ).
Les paramètres de cette étude en modélisation de la base sont: H
La longueur de diffusion des électrons Ln
D = 26 cm 2/s
=
=
300 ~m, NA
=
JO 16cm-3.
100 ~m et le coefficient de diffusion des électrons
n
La figure (1-2) représente le profil de la densité des porteurs générés dans la base de
différentes photopiles' caractérisées par leur champ cristallin E (en VIcm) pour une vitesse de
recombinaison nulle des porteurs à la jonction.
9
8°1013 r------r--I----...,..I--------,
-
·.~c
-
0
'-~\
'"
",.
-
.j
o
o
GOI
x(cm)
0.02
0.03
Figure (1-2): Densité des porteurs dans la base en fonction de la profondeur au voisinage du
circuit ouvert (SFn = 0 cm/s) et SB = 1Q3 cmls pour différentes photopiles
La figures (1-2) montre que pour une faible valeur de la vitesse de recombinaison SF n
des électrons à la jonction, le gradient des porteurs est inférieur ou égal à zéro.
Elle montre aussi que pour différentes photopiles caractérisées par leur champ cristallin, le
maximum de la densité des porteurs est d'autant plus élevé que le champ électrique cristallin est
faible.
Sur la figure (1-3), nous représentons le profil de la densité des porteurs pour SF n = 103 cmls.
6°10
13
1
1
'\
'\
,.-..,
M
1
E
u
'-"
en
....
~01013
\
\
\
f-
-
\
::l
Il)
t
"
0
CI..
en
""0
~
'\E= 0
.'-.,
Il)
"'-,'-,
2'\0 13 -
-
""-..'--,
E=5
'Vi
cIl)
-"'" ..... ~
:~~-
~
'E,~
15
.....,.. "i -'_..~ -
~
.. -"
L
........... "
0
0
0.01
0.02
0.03
x(cm)
Figure (1-3): Densité des porteurs dans la base en fonction'
de .la profondeur pour SFn
.
cmls el' SB = 103 cmJs pour qifférentes· photopiles
=
10 3
10
La figure (1-3) montre que pour le point de fonctionnement considéré (Sf n = 103 c m/s)
le profiJ de la densité des porteurs n'est pas modifié comparativement à celui pour lequel la
vitesse de recombinaison des porteurs à la jonction est nulle.
Les figures (1-2) et (1-3) montrent que pour ces points de fonctionnement, les porteurs
ne peuvent pas traverser la jonction. Ils restent stockés à cet endroit. Les photopiles
fonctionnent alors en circuit ouvert.
La figure (1-4) représente le profil des porteurs générés dans la base de la photopile
pour une valeur élevée de la vitesse de recombinaison des porteurs à la jonction.
8"1012 .-------.,...'---------,---'-------,
=5
'-.
\.
h~c
15
" '--.
o
o
0.01
0.02
0.03
x(cm)
Figure (1-4): Densité des porteurs dans la base en fonction de la profondeur au voisinage du
court circuit (Sfn = 10 8 cm/s) et SB = 106 cm/s pour différentes photopiles.
La figure (1-4) montre que pour un champ électrique donné, la densité des porteurs
présente trois régions:
- Une première région proche de la jonction où le gradient des porteurs est positif. Les
porteurs situés dans cette' région peuvent donc traverser la jonction et participer à la
production du courant.
- Une deuxième région où le gradient des porteurs est nul.
- Une troisième région où le gradient des porteurs est négatif Les porteurs qui se trouvent
dans cette région ne participent pas à la production du courant. Ils se recombinent en volume
ou en face arrière.
Il
La figure (1-4) montre également quej pour plusieurs valeurs du champ cristallin, le
maximum de la densité des porteurs diminue lorsque le chanip cristallin augmente et se déplace
vers la jonction. Cela se traduit par un élargissement de la zone de charge d'espace. En effet, le
maximum de la courbe de densité des porteurs défirùt un gradient nul. Les porteurs générés
·dans la première région peuvent traverser la jonction. Par contre, pour les porteurs générés
dans la troisième région, le gradient est négatif Ces derniers ne peuvent pas traverser la
jonction. Pour la photopile, ces porteurs semblent donc être en position de circuit ouvert. Tout
se passe comme si la base de la photopile se réduisait d'une quantité équivalente à la distance
entre la jonction émetteur/base et le maximum de la courbe de densité des porteurs, d'où un
phénomène qui ressemble à un élargissement de la zone de charge d'espace.
Les figures (1-2), (1-3) et (1-4) montrent que le circuit ouvert, le court circuit et les autres
points de fonctionnement de la base de la photopile sont obtenus par variation de la vitesse de
recombinaison à la jonction. Ainsi, la densité des porteurs est une fonction de la vitesse de
recombinaison des électrons à la jonction.
Dans les figures (1-5) et (1-6), nous présentons les densités relatives des porteurs en
fonction de profondeur pour une base quasi-neutre ( E
=
aV/cm) pour différentes valeurs de la
vitesse de recombinaison SF n des porteurs à la jonction.
0.5
1
1ei-"··.,
0.015
0.03
x(cm)
Figure (1-5): Densité relative des porteurs en fonction de la profondeur x pour différentes
valeurs de SF n avec SB = 4.10 4 cmls
La figure (1-5) montre que lorsque la vitesse de recombinaison SF n à la jonction des
-porteurs photogénérés augmente ( pour SB fixée ), le maximum de la courbe de densité des
, porteurs s'éloigne de la jonction. Ce phénomène a déjà été observé sur la figure (1-4)' et il a été
interprété comme un élargissement de la zone de charge d'espace.
12
Ainsi, la zone de charge d'espace a une épaisseur plus importante au voisinage du court circuit
qu'au voisinage du circuit ouvert pour une photopile donnée. C'esî également le phénomène
qui est observé dans les photopiles dans lesquelles le champ cristallin est croissant.
La figure (1-6) représente le profil de la densité relative des porteurs pour différentes
valeurs de la vitesse de recombinaison des porteurs SB sur la tàce alTière pour le même point
de fonctionnement pour une photopile donnée.
•
\
\
0.5
0.001
o
0.015
0.03
x(cm)
Figure (1-6): Densité relative des porteurs en fonction de la profondeur x pour différentes
valeurs de SB avec SF n = 3.103 cm/s
La figure (1-6) montre que le maximum de la densité des porteurs demeure
pratiquement situé à la même position lorsque la vitesse SFn est maintenue constante, avec SB
variable. La seule variation de SB n'introduit pas une variation sigruficative de la densité des
porteurs à la jonction.
III ETUDE DU COURANT DANS LA BASE DE LA PHOTOPILE
Dans ce paragraphe, nous faison~.une étude en modélisation du photocourant délivré.
par la base de la photopile. Ce photocourant est dû à la circulation des électrons qui traversent
la zone de charge d'espace.
Nous étudierons le photocourant pour différents points de fonctionnement de la photopile (
déterminés par la vitesse de recombinaison des porteurs SFn il la jonction ).
Au cours de cette étude, l'influence du champ électrique cristallin et des phénomènes de
recombinaison aux interfaces sur la densité de courant sera mise en évidence.
Nous nous intéresserons enfin à l'influence de la vitesse de 'recombinaison des porteurs SB à la
face arrière sur la densité de courant.
13
A partir de la densité des porteurs générés dans la base de la photopile, nous déduisons
la densité de photocourant des électrons par l'équation suivante [1-15]:
]
n
l
= q D
an
n
(x)
_ + ~ . n ( 0) . E
Ix=O
n
p
-p_---J
(lx
]
(1-9)
aO) Photocourant en fonction de SF n
En injectant la condition à la limite (1-6) dans l'équation (1-9), celle-ci peut être reécrite sous la
fonne suivante:
-.
]
n
-
=q(SF
n
+~l n E)n p (0)
(1-10)
A l'aide de l'équation (1-10), nous représentons sur la figure (1-7) les courbes de densité de
courant des électrons en fonction de leur vitesse de recombinaison SF n à la jonction pour
différentes photopiles caractérisées par leur champ cristallin E.
0035
"
/
---E-",j---
__ ..E=fL
/
E= 1;4
/
/
1
/
1
il
0.018
1
!
/
/
1
/1
- <~_/
/
.
1
---.L
-'
4.25
log(Sfn)
Figure (1-7): Densité de photocourant d'électrons dans la base en fonction de SFn pour
différentes photopiles av~ SB
=
OcmJs.
La figure (1-7) montre que la densité de photocourant des électrons est minimale pour
SFn tendant vers zéro et elle atteind sa valeur maximale lorsque SFn tend vers l'infini _
Ainsi, au voisinage du court circuit ( pour lequel le gradient à la jonction des porteurs générés
dans la base est positif), le courant.est maximal tandis qu'il est minimal au voisinage du circuit
-
.
14
ouvert. Ceci est en accord avec le fait qu'en court circuit, les électrons générés près de la
jonction la traversent, ce qui n'est pas le cas en circuit ouvert.
La figure (1-7) montre également que les densités de photocourant dans la base
dépendent du champ cristallin . Le photocourant croît dans le même sens que le champ
cristallin. La composante du champ cristallin qui contribue à l'augmentation du photocourant
est la composante suivant x, car dans notre modèle (modèle unidimensionnel), seuls les
électrons qui traversent la zone de charge d'espace participent au photocourant
En faisant varier SB, nous obtenons les profils suivants:
""i).a3~
.. E~5·
,-....
Ë
u
:;;:
........,
.---__----E.-=-.Q-
Vl
C
f
0
l-<
.....
1
U
f
~
1
<l)
Vl
<l)
/'
1
1
1
1
O.a17
"0
/
~
1
1
l-<
1
1
;:::l
0
u
0
.....
0
/
...c:
/
/
0..
/'
1.131°10-5
'---=-""'='--
a
.L..-
~.25
-----'
8.5
log(SFn)
Figure (I-8): Densité de photocourant d'électrons dans la base en fonction de SFn pour
différentes photopiles avec SB = I03 c m/s
15
--.
~t--
0.034
CSu
E = (5 .
:<
'-'
!
Cf}
c:
..
.
..
(
._-------I;-=-O---
//
,
U
tl)
~
/
/
o....
~
.. E=.!)
f
0.017 r-
-
;
/
/.
~:;
/
o
/il
:.
' :
U
;'
S
~
0...
,/
1.119 °
/
!
!
)
/
- 5 L...-""'-'-/-"'~="':::.,'
",,'-,', , - - - - - , - - : - ' - - - ' : - - - ' - - - - - - - '
10
o
8.5
4.25
log(Sfn)
Figure (1-9): Densité de photocourant des électrons dans la base en fonction de SFn pour
différentes photopiles avec SB
=
10 6cm/s.
Les figures (1-8) et (1-9) montrent que le photocourant est faiblement influencé par les
variations de la vitesse de recombinaison des porteurs à la face arrière de la base de ia
photopile. En effet, lorsque SB varie de
° à 106cm/s, nous n'observons pas une variation
significative de la densité de courant. Ceci s'explique par le fait que SB intervient dans la
densité de courant ( équation (1-10) ) par l'intermédiaire de la densité des porteurs, et nous
avons déjà observé dans la figure (1-6) que pour un point de fonctionnement donné, les
variations de SB n'influencent pas le gradient des porteurs générés à la jonction de la photopile.
Les figures (1-10) et (1-11) représentent la variation de la densité de photocourant en
fonction de SFn pour différentes photopiles caractérisées par leur champ cristallin et pour une
vitesse de recombinaison aux interfaces SFO n .
0.034 . - - - - - - - - ' ' ' ' - - - - ,J..~-:::::-=-------,
'E""S'
/
Cf}
c:
o....
U
tl)
~
Cf}
!
0.018 >-
tl)
-0
-
/j
/
~....
/
!
;:l
o
u
o
o
..c:
0...
1
0.001
a
4.25
85
log(Sfn)
Figure (1-10): Densité de photorourant d'électrons dans la base en fonction de SFn pour
diffé~.entes photopiles ~vec SFO n -= 102cm/s et SB = 103 cm/s.
]6
L~'­
0.0:4
:......-v
If'
/
E=O
!
/
,..
1
1
Vl
c:
J
./
o
/
......
...U
(l)
:a3
Vl
0.021-
//
(l)
-0
§......
::i
o
o
...o
..c:
u
0....
./
0008
o
/
-
1
4.25
~.5
log(SFn) -
figure (1-] 1): Densité de photoCQurant d'électrons dans la base en fonction de SFn pour
différentes photopiles avec SfO n = 103 cm/s et SB = 10 3cm/s.
Les figures (1-] 0) et (1-] ]) montrent que lorsque SFn tend vers zéro (au voisinage du
circuit ouvert), la densité de courant n'est pas nulle mais prend une valeur qui dépend de la
valeur de SfO n' Ainsi, lorsque SfO n augmente, la densité de courant augmente. Ceci indique
qu'il existe un courant résiduel dû à SfO n .
SFO n caractérise les effets des états d'interface dans la base. Elle se traduit par une perte de
porteurs de charge comme dans une résistance shunt. Le courant résiduel passera à travers
cette résistance shunt. C'est un courant de fuite. Il est d'autant plus important que les
recombinaisons aux interfaces sont importantes.
La figure (1-] 2) représente l'action des recombinaisons aux interfaces sur le
photocourant pour différentes photopiles.
r--..
N
0.03r'-----'------'1,.. -....-...-...-.- - ...-...-.-_..---.---'
...
$
S
""j
u
-;
~
... ~~.~~1 e4
. ./ ;'
,
li>
c:
J
o
.b
u
1
t
1
cu
1
:a3
~
r
O.ülS-
-0
(
(
~
:
g
(
,1
u
.2
..2
P-i
2.26~1O-s
-
/
1/
SFOn=le.2,f
: ; / SFOn=O
L--_=
o
1
...L.-
S
-'
10
log(SFn)
Figure (1-] 2): Densité de photocourant dans la base en fonction de SFn pour différentes
valeurs de SFOn
17
La figure (1-12) montre que lorsque les recombinaisons aux interfaces sont importantes,
( grandes valeurs de SfOn ), les pertes de courant sont aussi importantes. Inversement, iorsque
les recombinaisons aux interfaces sont faibles, les courants de fuite sont également faibles.
Pour une photopile de bonne qualité, les recombinaisons SfO n liées aux interfaces sont faibles.
Pour une photopile de mauvaise qualité, les recombinaisons liées aux interfaces sont
importantes.
Lorsque la photopile fonctionne en court circuit, les recombinaisons SfO n liées aux interfaces
subsistent mais elles sont masquées par les recombinaisons Sf 1 liées à la charge externe de la
photopile.
bO) Photocourânt en fonction de SB
Dan ce paragraphe, nous étudions l'influence de la vitesse de recombinaison SB des
porteurs à la face arrière de la base sur le photocourant.
Nous représentons sur la figure (1-13) la variation de la densité de photocourant en fonction de
SB pour différentes photopiles caractérisées par leur champ cristallin E.
1
··E·"5···
-
-
1
4
8
fog(S13 )
Figure (I -13): Densité de photocourant d'électrons dans la base en fonction de SB pour
différentes photoni!es
avec SF n = 103 crPJs.
•
Pour une valeur donnée de la vitesse de recombinaison SB, le photocourant est plus
important lorsque l'on passe d'une photopile à champ cristallin faible à une photopile à champ
cristallin élevé. Le champ cristallin accélérateur des électrons a donc pour effet d'augmenter le
photocourant. Ce phénomène a déjà été observé dans le paragraphe précedent.
18
La figure (1-13) indique également que l'influence de la vitesse de recombinaison des porteurs
SB à la face arrière sur la densité de courant, bien que faible, devient de plus en plus
perceptible lorsque le champ cristallin devient important Dans les photopiles dont la base est
considérée comme quasi-neutre ( E = OV/cm ), l'influence de SB sur Je photocourant n'est pas
observée.
La figure (1-14) représente la variation du photocourant de la base en fonction de la
vitesse de recombinaison SF n à la jonction des électrons pour trois valeurs de SB ( Ocmls,
2.10 2 cmls, 4.1 04cmls ) pour un champ cristallin nul.
SB=OL.~o-··A~;;;.fè4---·"·"
0.03
-
(
SB=:l~:l
,
.1
ç:
'"
o
b
.
u
cu
.
:qJ
cu
'"
-0
0.015
f
1-
-
~
~
o
....o
u
/
o
/
..c::
Çy
o
o
1
4.25
8.5
Iog(SFn)
Figure (1-14): Densité de photocourant des électrons dans une base quasi-neutre en fonction de
SF n pour différentes valeurs de SB (0,2.10 2 , 4.104 cmls).
La figure (1-14) montre que pour différentes valeurs de la vitesse de recombinaison SB
des électrons à la face arrière, la densité de photocourant est invariante lorsque SB augmente.
Ceci est également observé dans les figures (1-7), (1-8) et (1-9). En effet, en comparant par
exemple la valeur du courant de court circuit pour la même valeur du champ cristallin (prenons
par exemple celle pour laquelle le champ a la valeur 15 volts/cm), la densité de courant de
court circuit est de 35 mNcm 2 pour SB = Ocmls tandis qu'elle vaut 34 mNcm 2 pour SB =
10 3 cmls. Il en est de même lorsque l'on examine le comportement de la densité de courant au
voisinage du circuit ouvert.
La figure (1-15) met en évidence la variation de la densité de photocourant des
électrons en fonction de SB pour une photopile dont le champ cristallin est fixé à OV/crn.
.
-
19
<g
0.008
'\
\\
u
~
'-"
Ul
c:
o....
U
(1)
1
c-----_
0.008
f-
\
-
"
\
"-<1)
\,
Ul
(1)
"
'""0
§.... 0.008
-
::l
o
U
o
'6
..c
0...
1
0.008
o
4
log(Sll )
Figure (1-15): Densité de photocourant des électrons dans une base quasi-neutre en fonction de
SB pour SFn = 10 3cm/s.
Sur la figure (1-15), nous constatons que les deux extrêmes du photocourant en
fonction de SB prennent la même valeur jusqu'au millième près. Le photocourant ne varie donc
pas de façon sensible en fonction de la vitesse de recombinaison sur la face arrière SB des
porteurs. En effet, les électrons générés sur la face arrière de la base ( loin de la jonction) ne
contribuent pratiquement pas à la production du photocourant. Ils se recombinent dans le
massif avant même d'arriver à la jonction émetteurlbase.
Les courbes de densité de photocourant en fonction de la vitesse de recombinaison à la
jonction SFn des porteurs ont montré qu'au voisinage du court circuit (grandes valeurs de
SF n), le photocourant est constant. Des études récentes [1-11, 16, 22] ont déjà mis en évidence
ce phénomène. Cela est traduit par l'équation (1-11):
al
aSFn
__n_=O
(1-11)
L'équation (1-11) admet deux solutions qui sont:
(1-12)
20
(1-13)
Ces solutions montrent que la viiesse de recombinaison sur la face arrière SB des
électrons dans la base peut prendre deux valeurs possibles dont l'une (SB 1) dépend seulement
des paramètres de la base et l'autre (SB2,i) dépend, en plus des paramètres de la base, de la
nature de la radiation excitatrice.
.
La solution SB 1 est proportionnelle, à un coefficient multiplicatif près ( th(H/L) ), à la
vitesse de diffusion DIL [1-17] (pour un éclairement monochromatique).
La solution SB2 ,i dépend des termes de génération bi. Elle sera alors assimilée à la
vitesse de génération.
Pour une radiation multispectrale, SB2 est l'effet cumulé de chacune des radiations
monochromatiques. Alors dans ce cas, cette valeur de SB2 est obtenue par sommation sur
toute la série de chacune des valeurs SB2 ,i.
Nous présentons surIes figures (I -16), (I -17) les variations des vitesses de
recombinaison SB 1 et SB2,i en fonction de l'épaisseur de la base.
3000
.--------
o
o
--_.-
0015
0.03
H(cm)
Figure (1-16): Vitesse de recombinaison SBI en fonction de H (Ln
=
O.Olcm et D n = 26cm 2/s)
21
l
J
1
l
o
o
1
0.03
0.015
H(cm)
Figure (1-17): Vitesse de recombinâison SB2,i en fonction de H (Ln
=
0.0 lcm et D n = 26cm 2 /s
pour les trois termes de la série.
La vitesse de recombinaison sur la face arrière SB des porteurs montre que pour
chaque terme
de
la
série,
les vitesses
de
recombinaison
SB 1 et
SB2,i
tendent
asymptotiquement vers une valeur limite aux grandes valeurs de l'épaisseur H de la base.
Dans le tableau (1-1), nous déterminons la valeur limite de cette vitesse pour une base
d'épaisseur H = 300Jlm et dont le coefficient de diffusion des électrons 0 = 26cm 2 /s.
Tableau (1-1): Calcul des vitesses de recombinaison en face arrière des porteurs de charge
SB] (cm/s)
2.587 J03
SB2 (cm/s)
SB2 (cm/s)
SB2 (cm/s)
i=1
i=2
i= 3
2.613 J03
2.616 J03
2.659 10 3
DIL (cm/s)
2.6 10 3
La vitesse de recombinaison limite des porteurs de charge à la face arrière est donc
proche de la vitesse de diffusion qui est de 2.6 J03 cm/s.
La figure (1-18) montre la variation de la vitesse de recombinaison pour l'ensemble du
spectre en fonction de l'épaisseur de la base
..
22
11
1.5 105.
!
1
~
U'l
Eu
'--"
\
Q)
......
1::
cd
......
""3
U'l
Q
1
'Q)
l-
1
I::
0
\
U'l
'Cd
1::
:..0
-
1 105
5-10
~\
4
E
0
u
1
Q)
l-
-
\
1
'"
Q)
'U
Q)
'"
U'l
Q)
......
>
a
a
'- ----'"--
-
T
0.015
-,----_ .. -
0.03
H(cm)
Figure (1-18): Vitesse de recombinaison pour l'ensemble du spectre de la radiation excitatrice
en fonction de H pour Ln = O.Olcm et On = 26cm 2/s.
Cette figure montre que la vitesse de recombinaison passe par une valeur maximale
lorsque l'épaisseur de la base augmente. Ce maximum se situe en dessous de 75 Jlm. Lorsque la
vitesse de recombinaison prend cette valeur, le photocourant n'atteindra pas sa valeur optimale,
en comparaIson avec le photocouram pour une valeur différente de la vitesse de
recombinaison.
Toutefois, cette dernière inquiétude est levée dans la mesure où les photopiles que nous
étudions (photopiles au silicium) sont des photopiles dont la base a une épaisseur comprise
entre 180 et 300 Jlm.
IV ETUDE DE LA PHOTOTENSION
Dans ce paragraphe, nous étudierons l'influence de la vitesse de recombinaison des
porteurs SF n à la jonction sur la tension délivrée par la base de la photopile.
Nous nous intéresserons également à l'action du champ cristallin sur la tension.
Nous étudierons enfin l'influence de la vitesse de recombinaison des porteurs SB à la face
arrière sur la tension.
L'application de l'équation de Boltzmann pour les faibles niveaux d'injection (dans la
base), nous permet de relier la densité des porteurs à la tension par:
23
(1-14)
Dans cette expression:
n (0) est la densité des porteurs minoritaires de charge créés dans la base en x =
P
o.
YT est la tension thermique. VT peut s'écrire Y = KT ou en tenant compte de la
T
q
D
mobilité J..l n des électrons, V = __ ...D_,
T
,un
. _ n.2
_
.
nO = _1- avec n- étant la conèentration intrinsèque .des électrons et NB est le taux
.p
N I , .
B
de dopage de la base en atomes d'impureté.
y est la tension délivrée par la photopile
La phototension est déduite de l'équation (1-14) par:
V
~
V ln\
T
:p
L
:0) + 11
(1-15)
np
aO) Phototension en fonction de SF n
L'expression de la phototension en fonction de Sfn est:
V(SFn)~
VTln
n (Sf)
p n~ n +1
l
1
(1-16)
La figure (1-19) représente la variation de la phototension en fonction de la vitesse de la
recombinaison des porteurs Sf n à la jonction pour différentes photopiles caractérisées par leur
champ cristallin.
24 .
s:::
o
'v)
s:::
-
0.341 -
~
.8
o
..s:::
0...
o
1
6.75
13.5
log(SFn)
Figure (1-19): Phototension en fonction de SF pour SB = 102 cm/s pour différentes photopiles
n
La figure (1-19) indique que la phototension est maximale pour les faibles valeurs de la
vitesse de recombinaison des porteurs à la jonction. Elle décroît lorsque la vitesse de
recombinaison augmente.
La valeur de phototension atteinte pour les faibles valeurs de vitesse de recombinaison des
porteurs à la jonction (qui définit le circuit ouvert) est la tension de circuit ouvert. C'est la
tension maximale que peut délivrer la photopile.
Aux grandes valeurs de la vitesse de recombinaison à la jonction des porteurs, la tension prend
une valeur nulle. En court circuit, la photopile ne délivre pas de tension.
La figure (1-19) indique également que pour différentes valeurs du champ électrique
cristallin, la tension de circuit ouvert est d'autant plus importante que le champ cristallin est
important. Le phénomène qui se produit est un stockage des charges à la jonction. Le champ
cristallin renvoie alors les charges vers la jonction.
bD) Phototension en fonction de SB
Nous avons représenté sur la figure (1-19) les variations de la phototension en fonction
de la vitesse de recombinaison à la jonction des électrons SF n pour une valeur de la vitesse de
recombinaison SB à la face arrière.
Sur la figure (1-20), nous représentons la variation de la phototension en fonction de SB pour
différentes photopiles caractérisées par leur champ cristallin E.
25
0.64
.--,
. .. _. __ E=_O___________ __
0.62
-
-
E=5
-
0.6 -
. . . E. === -lS. --- -- 1
0.58
o
5
tO
15
log(SB)
Figure (1-20): Phototension en fonction de SB pour SF n = 10 3cm/s pour différentes valeurs de
E (en V/cm)
Les courbes de la figure (1-20) indiquent que la phototension varie peu lorsque la
vitesse de recombinaison SB augmente. Néanmoins, en faisant une analyse plus approfondie,
nous constatons que la tension délivrée par la photopile diminue lorsque la vitesse de
recombinaison à la face arrière des électrons augmente. Cela est beaucoup plus perceptible
-POUf
un champ cristallin important.
V
ETUDE EN MODELISATION
DE LA CARACTERISTIQUE COURANT-
TENSION DANS LA BASE
Les études du courant et de la tension ( paragraphes III et IV ) délivrés par la photopile
éclairée par une lumière blanche indiquent que ces deux paramètres macroscopiques dépendent
de-la vitesse de recombinaison SFn à la jonction des porteurs.
En reliant ces deux paramètres à l'aide du paramètre phénoménologique SF n , nous pouvons
observer simultanément leur comportement.
La figure (1-21) représente les caractéristiques courant-tension obtenues dans la base
pour différentes photopiles caractérisées par leur champ cristallin E.
26
0.034
15
E\-~
---
0 ------ ------ -------------------------------"
\
---~-E-o.
\
\
<Il
\
\
tî
\
~
\
t::
o
....
li)
00\7
f-
\
i
IL
li)
\
-0
\
~....
\l:
<Il
\
\
\
\
:-
:J
o
u
\
\
S
o
..c
\
1
0..
1
1
O.6R2
034\
phototension (V)
Figure (1-21): Caractéristiques courant-tension de la base pour SB
=
10 6 cm/s pour différentes
photopiles.
La figure (1-21) montre que lorsque la tension délivrée par la photopile est minimale, Je
courant est maximal: C'est le cas où ta photopile fonctionne en court circuit. Inversement,
lorsque la tension délivrée par la photopile est maximale, le courant est minimal: Ceci est Je cas
où la photopile fonctionne en circuit ouvert.
Par ailleurs, ces caractéristiques montrent l'influence du champ électrique cristallin sur
le courant et la tension que délivre la photopile. Lorsque le champ électrique augmente, le
courant de court circuit augmente. Il en est de même pour la tension de circuit ouvert. Le
champ électrique accélérateur d'électrons a pour effet d'augmenter le courant de court circuit et
la tension de circuit ouvert.
VI LE COURANT DE DIODE
En reécrivant l'équation (I-I 0) en tenant compte de l'équation (1-7), il vient que:
J n (SFn ) = q(SFO n + ~lnE}np (0) +q. SF1n p (0)
(1-16)
Posons:
(I - 17)
et
Jt(SFn)=qoSFlonp(O)
(1-18)
où Jt(SF n) est le courant qui traverserait la résistance de charge externe et h(SF n) est le
courant qui est-perdu à cause des phénomènes d'interface:
L'équation (1-18) se reécrira:
27
:
o[ (YJ ]
Jf(SFn )=q·(SFO n +!l Il ·E)·n p exp --.
--1
V
T
(1-19)
En circuit ouvert, nous faisons les hypothèses suivantes:
2°) SF 1 «(SFO n + !lnE)
De la première hypothèse. il vient que: J f (SF n
Et ~e la" seconde hypoth~se: h(SF n)
1
)~ q . (SFü n + fi P . E) . n ~ [expl ~ J
» Jt(SF n), ce qui conduit à J n (~Fn) ~ J f (SFn). Ainsi,
le photocourant se réduit au courant de fuite.
Ce courant de fuite, qui est relatif à la vitesse de recombinaison aux interfaces, peut
être décomposé de la manière suivante:
J (SF )
f
n
= J d (SFn ) + J r (SF n )
(1-20)
où
J d (SF n )=q-SFO n
.no[exP(~.]-l]
p
V
T
(1-21)
et
(1-22)
Jd(SF n) est la fraction du courant de fuite de la photopile sous éçlairement
correspondant à un courant de diode sous obscurité.
JrCSFn) est la fraction du courant de füite qui traverserait une résistance placée en parallèle
avec la diode. C'est le courant de saturation 11-16].
En court circuit, nous pouvons faire l'hypothèse suivante: SF 1 » (SFO n + !lnE), ce qui
conduit à: J n (SFn) ~ J t (SFn ). Dans ce mode de fonctionnement alors, le photocourant est
presque entièrement délivré dans le circuit extérieur
Dans un mode de fonctionnement intermédiaire, les recombinaisons liées aux effets
d'interface et celles liées à la résistance de charge externe sont à prendre en compte.
28
Sur la figure (1-22) nous représentons la variation du courant de diode en fonction de la
phototension pour SFO n = 102 cm/s.
N
0.006
1
E
:<u
1
1
1
'-"
~
1
~
'c:
:::1
u
0.003
J
-
{
t1
~
1
..D
1
o
i
~
§
~
8
i
1. 894'10
14
l'
~//
'----:.-----"-----'----=~----'
0.341
0.006
0.677
Phototension (V)
Figure (1-22):Courant de diode en fonction de la tension V pour SFO n = I02cm/s.
Le courant de diode est obtenu à partir de la densité des porteurs photogénérés. Il est
faible lorsque la tension délivrée par la photopile est faible cette situation se produit au
voisinage du court circuit. Au voisinage du circuit ouvert, le courant de diode devient
important de même que la tension de circuit ouvert.
Les vitesses de recombinaison induites par les états d'interface masquent celles qui sont
introduites par la charge externe en circuit ouvert. Si ces recombinaisons interfaciales sont
importantes, la photopile sera de mauvaise qualité et la tension de circuit ouvert qu'elle délivre
sera faible. Par contre, si les recombinaisons interfaciales sont faibles, la photopile sera de
bonne qualité et la tension de circuit ouvert qu'elle délivre sera élevée.
En court circuit par contre, il se produit l'effet contraire à savoir que ce sont les vitesses de
recombinaison introduites par la charge externe qui masquent celles induites par les états
d'interface. Cependant, les recombinaisons liées aux interfaces subsistent et déterminent la
qualité de la photopile.
VU PUISSANCE ELECTRIQUE DELIVREE PAR LA BASE DE LA PHOTOPILE
Ce paragraphe est consacré à l'étude en modélisation de la puissance électrique
produite par la photopile. Nous étudierons l'influence de la vitesse de recombinaison des
porteurs SFn à la jonction sur la puissance de la photopile. Nous examinerons aussi les effets
des phénomènes d'interface et du champ cristallin sur cette puissance.
Lorsque la photopile est en fonctionnement, divers. processus de pertes limitent ses
perfonnances ( pef!es ·Iiées à la structure du matéria.u, pertes au niveau des int~rfaces
29
émetteurlbase, faces externes de la base) [1-11]. Nous ne tiendrons compte que des pertes liées
au paramètre phénoménologique SFû n.
Nous avons évalué dans les paragraphes (III) et (IV) le courant et la tension délivrés par la
photopile.
La puissance délivrée par la photopile est donnée le produit des deux grandeurs
précédentes.
Ainsi, nous écrivons:
(1-23)
Dans cette expression:
P(SF n) est la puissance délivrée par la base de la photopile en fonction de la vitesse de
.reco mb-inai son des porteurs à la jonction
Jt(SF n) désigne le courant délivré au circuit extérieur en fonction de la vitesse de
recombinaison des porteurs la jonction
V(SF n) désigne la tension en fonction de la vitesse de recombinaison des porteurs la
jonction
Nous représentons sur la figure (1-23) la variation de la puissance délivrée par la base
pour différentes photopiles caractérisées par leur champ cristallin en fonction de la vitesse de
recombinaison des électrons à la jonction:
o
6.75
log(SFn)
13.5
.
.
Figure (1-23): Puissance délivrée par la base en fonction de SF n pour SFû n = ûcmls pour
différentes photopiles avec SB = l û3em/s.
La figure (1-23) montre que la puissance délivrée par la base de la photopile est faible
lorsque celle-ci fonctionne en court circuit ou en circuit ouvert. Elle passe par un maximum qui
est situé en un point de fonctionnement intennédiaire. Ce point de fonctionnement pour lequel
30
la puissance est maximale se déplace vers le circuit ouvert lorsque le champ électrique cristallin
est élevé.
La figure (1-23) montre également que lorsque le champ électrique cristallin est élevé,
la puissance délivrée par la base de la photopile augmente. Ce phénomène tire son origine de
l'orientation que nous avons attribuée à la composante suivant l'axe (ox) ( figure (1-1) ) du
champ cristallin: En effet, pour un vecteur champ cristallin orienté de la jonction vers la face
arrière de la base ( x > 0 ), son action est de renvoyer les électrons générés vers la jonction.
Sur la figure (1-24), nous représentons la variation de la puissance délivrée par la base
de différentes photopiles caractérisées par des recombinaisons introduites par les états
d'interface.
,
0.015
,
1
SFOn=le2 r~"
1
/
1
:!
1
.
,
.
;i
1
•
r ,
0.005 -
-
:i
'.
. J
'"
... SFOn=le4
.....J././
'.
1
8.5
17
log(SFn)
Figure (1-24): Puissance délivrée par la base en fonction de SF n, pour SB
différentes valeurs de SFO n
La figure (1-24) montre que les recombinaisons liées aux
=
interf~-lces
103 cmJs et pour
ont pour effet de
diminuer la puissance de la photopile. En effet, pour deux photopiles données, la puissance
maximale de celle dont les effets d'interface sont faibles sera plus importante que pour celle
dont les effets d'interface' sont élevés. Les états d'interface déterminent la qualité de la
photopile.
La puissance et la tension ont une variable commune qui est la vitesse de recombinaison
SF n à la jonction des porteurs. Nous pouvons donc étudier simultanément le comportement de
la puissance en fonction de la tension à l'aide de cette vitesse de recombinaison
Sur la figure (1-25), nous représentons la variation de la puissance en fonction de la
tension pour différentes ph,?topiles caract.éris~es par leur champ cristallin E.
31
0.02
./
E = 15/
"
/
,//
/
/
/
·E:::C··5 \\
-',
\
\
\
1
1
/
./
0.01
1
1
1
1
1
1
1
o
0.344
0.006
0.682
Phototension (V)
Figure (1-25): Puissance délivrée par la base en fonction de la tension pour différentes
photopiles avec SB = 10 3cm/s.
La figure (1-25) nous indique que la puissance électrique délivrée par la base de la
photopile augmente linéairement aux faibles valeurs de la tension, atteind un maximum et
décroît rapidement au voisinage de la tension de circuit ouvert. Le maximum de puissance se
rapproche de la tension de circuit ouvert pour les champs cristallins élevés. Ce constat a déjà
été fait sur la figure (1-23).
La détermination de la valeur de la vitesse de recombinaison à la jonction pour laquelle
la puissance électrique délivrée par la photopile est maximale se fait par la résolution de
l'équation suivante:
ùP(SF )
__ ..
?SF
n__ = 0
n
(1-24)
L'équation (1-24) est une équation transcendante dont la résolution peut se faire
graphiquement.
VIII RESISTANCE DE CHARGE DE LA PHOTOPILE
Dans ce paragraphe, nous faisons une étude en modélisation de la résistance de charge
'de la photopile. Nous étudierons l'action de la charge externe sur le point de fonctionnement de
la photopile...
32
D'après l'équation (I-7), I~ point de fonctionnement de la photopile peut être détenniné par SF 1
qui est définie comme la vitesse de reéombinaison à la jonction des porteurs introduite par la
charge externe de la photopile. Dans le paragraphe (IV), Jt(SF n) est le courant délivré au
circuit extérieur dont la résistance est la résistance de charge externe.
La résistance de charge externe peut alors être obtenue à l'aide de la relation (1-25):
(1-25)
La figure (I-26) représente les variations de la vitesse de recombinaison
d~s
p0r:!.eurs à
la Jonction en fonct}on de la 'résistance de charge externe d'une ph~)topile dont la base est
considérée comme quasi-neutre.
1
2.75
~
~
\
-
~\
1.375
00
\
.Q
,
'-,
..............
"
'" .._-~
1
o
-.-----
- - - - . . - -_ _
119.41
Résistance de charge (o.cm2)
Figure (I-26): Vitesse de recombinaison à la jonction en fonction de la résistance de charge
pour SFO n = Ocmls pour une base quasi-neutre.
La fibTlJre (1-26) montre que pour de grandes valeurs de résistance de charge externe de
la photopile, la vitesse de recombinaison à la jonction des porteurs générés est faible. Et
inversement, pour de faibles valeurs de résistance de charge, la vitesse de recombinaison des
porteurs est élevée.
Ainsi, lorsque la charge externe de la photopile a une résistance élevée, la vitesse de
recombinaison ( induite par cette charge externe) à la jonction des porteurs est faible Les
porteurs som donc stockés à la jonction. Dans ce cas, la photopile fonctionne en cîrcuit ouveI1.
Pour une valeur faible de la résistance de charge, la vitesse de recombinaison ( introduite par la
charge externe) à la jonction des porteurs est élevée. Ils peuvent donc traverser la jonction et
être collectés par les grilles. La photopile fonctionne alors en court circuit.
33
La figure (1-27) représente la variation du point de fonctionnement d'une photopile
caractérisée par les recombinaisons introduites par les étais d'interface en fonction de la charge
externe.
4.5
""- "-
-.,
"
~."'''--
~-.,~........ _~....
"2
I-Ll
{()
'-"''''''
"
).)5
"---'
--
.....
00
,
\
..s
0
\
1
)0.618
50309
·.80
Résistance de charge (O.cm2)
Figure (I-27):Vitesse de recombinaison à lajonction en fonction de la résistance de charge
pour SFO n = 10 3 cm/s.
La figure (1-27) montre que lorsque l'on prend en compte les états d'interface, la valeur
de la résistance de charge pour laquelle la photopile fonctionne en circuit ouvert est faible,
comparée a celle de la figure (1-26). Il en est de même pour la valeur de la résistance qui
détermine le fonctionnement en court circuit de la photopile. Cette figure montre aussi que la
résistance de charge atteind une asymptote au voisinage du circuit ouvert.
Enfin, la qualité de la photopile étant déterminée par les états d'interface, la tension de
circuit ouvert sera élevée pour une photopile de bonne qualité et elle sera faible si la photopile
est de mauvaise qualité. Il en sera de même pour le courant de court circuit.
IX
ETUDE DE LA CAPACITE DE L'ELARGISSEMENT DE LA ZONE DE
CHARGE D'ESPACE
Dans ce paragraphe, nous faisons une étude en modélisation de la capacité de
l'élargissement de la zone de charge d'espace en fonction du point de fonctionnement de la
photopile.
Lorsque le champ cristallin diminue, nous avons
obselY~
que la zone de charge d'espace
. s'élargit (figures (1-2), (1-3), et (1-4)). Ce phénomène a également été observé sur l'étude de la
densité des porteurs lorsque la vitesse de recombinaison SF n à la jonction des porteurs
augmente (figure (1-5)).
Des études de régimes transitoires du courant de court circuit et de la tension de circuit ouvert
[1-18 .. 20] font apparaître des effets liés aux capacités inteI}lesde la cellule sur les courbes de
.courant ou de .tension.
· ...... ~
34
En ne faisant intervenir que les modificatiom; de la densité des porteurs stockés dans la base [121], il est possible d'évaluer la capacité de l'élargissement de la zone de charge d'espacé.
La quantité de charge électrique totale Q stockée à la jonction est:
Q " q. np(O)
(1-26)
où q est la charge d'un électron et np(O) est la densité des porteurs à la jonction ( en x = 0 )
La capacité Cp de l'élargissement de la zone de charge d'espace de la photopile est donnée par
la relation classique:
(1-27)
Cp == Q/V
Dans cette relation, V est la tension délivrée par la photopile à la jonction.
-
.
La figure (1-28) montre la variation de la capacité de l'élargissement de la zone de
charge d'espace de la photopile en fonction de la vitesse de recombinaison des porteurs Sf n à
la jonction pour une base quasi-neutre.
figure (1-28): Capacité l'élargissement de la zone de charge d'espace en fonction de Sf n pour
SB ~= l03 cm / s
La figure (1-28) indique que lorsque la vitesse de recombinaison Sf n à la jonction des
porteurs est faible ( voisinage du circuit ouvert, Sf n ~ 0 ), la capacité de la jonction atteind sa
valeur maximale tandis qu'elle est presque faible pour les valeurs de Sf n élevées.
En circuit ouvert, les portqJrs de charge générés ne traversent pas la jonction. Ils sont stockés
de part et d'autre de cette jonction et elle est ainsi assimilable à un condensateur. En court
circuit ( grandes valeurs de Sfn ), les porteurs générés dans la photopile traversent la jonction
et sont collectés par les grilles. Dans ce dernier cas alors, il n'y a pas de stockage de charge,
d'où une capacité faible.
35
En tenant compte ( pour l'étude d,e la capacité de la jonction) du comportement de la
densité des porteurs en fonction de la profondeur de la base pour différentes valeurs de SF n, il
apparaît qu'un élargissement de la zone de charge d'espace ( qui est une conséquence d'une
augmentation de SFn ) se traduit par une diminution de la capacité de la jonction alors que le
rétrécissement de cette zone ( conséquence d'une diminution de SF n) augmente sa capacité.
En conclusion, nous pouvons dire que pour une photopile fonctionnant en circuit
ouvert, l'élargissement de la zone de charge d'espace est faible et sa capacité est élevée tandis
que cet élargissement est plus important et la capacité devient faible pour une photopile
fonctionnant en court circuit.
CONCLUSION
L'étude de la base de la photopile nous a montré que lorsque la charge externe introduit
une vitesse de recombinaison faible comparée à cel1e qui est induite par les états d'interface, (
Sf 1 « SfO n ), la vitesse de recombinaison introduite par les états d'interface masque cel1e qui
est due à la charge externe. Dans le cas contraire ( SF 1 » SfO n ), la vitesse de recombinaison
des porteurs introduite par la charge externe masque celle qui est induite par les états
d'interface.
Lorsque la photopile fonctionne en court circuit, les vitesses de recombinaison Sf n à la
jonction des porteurs sont élevées et la zone de charge d'espace s'élargit.
La capacité de l'élargissement de la zone de charge d'espace est d'autant plus faible que
la vitesse de recombinaison Sf n est élevée. Les faibles capacités se retrouvent donc en court
circuit (élargissement de la zone de charge d'espace important) tandis qu'en circuit ouvert
(élargissement de la zone de charge d'espace moins important), les capacités sont importantes.
Cette étude a également montré que le champ électrique cristallin contribue à
augmenter la puissance de la photopile. Par contre, un champ cristallin faible a pour effet de
rétrécir l'élargissement de la zone de charge d'espace.
L'étude a enfin montré que des paramètres intrinsèques à la photopile limitent ses
performances. Ce sont essentiellement des paramètres qui tirent leur origine des phénomènes
de recombinaisons aux interfaces. Du point de vue électrique, nous avons associé au paramètre
phénomé~ologique
SfO n ( qui définit les états d'interface) une diode et une résistance shunt.
Ce paramètre phénoménologique détermine la qualité de la photopile.
36
BIBLJ[OGRAPHlE
[1-1]: A. CUEVAS, A. LUQUE, 1. EGUREN, J DEL ALAMO
"High Efficiency Bifacial Back Surface Field Solar CeUs" Solar Cells, Vol. 3, n04, pp. 337-340
198]
[1-2]: 1. DEL ALAMO, 1. EGUREN, A. LUQUE
"Operating Limits of Al-alloyed High-Low JUllctions for B.S.F. Solar Cells" Solid State
Electron. Vol 24, nOS, pp. 415-420, 1981
[1-3]: 1. EGUREN, 1. DEL ALAMO, A. LUQUE
"Optimisation ofp+ Doping Level ofn+ p p+ bifaèial B.S.F. Solar Cells By Ion Implantation"
Electron. Letters Vol. 16, n016, pp.633-634, 1980
[1-4]: A. LUQUE, 1.M. RUIZ, A. CUEVAS, 1. EGUREN, 1. SANGRADOR 1.M. AGOST
GOMEl, G. SALA, 1. DEL ALAMO.
"Static Concentrated Array With Double Side IIIuminated Solar Cell" Energia Solare e Nuove
Prospettive. Comples., Conferenza Intrenazionale., Milano, lTALlA, Vol. 1, pp 421-429 1980
[1-5]: G. C. JAIN, S. N. SINGH and R. KOTNALA
"Diffusion Length Determination In n+ p p+ Structure Based Silicon Solar Cells From the
Intensity Dependence of the Short Circuit CUITent for Illumination from the p+ Side" Solar
Cells 8 239-48, 1983
[1-6]: S. K. SHARMA, S. N. SINGH, B. C. CHAKRAVART Y and B. K. DAS
"Determination of Minority Carrier Diffusion Length in p-Silicon Wafer By PhotocuITent
Generation Method" 1. App!. Phys. 60 (10) pp. 3550-52, 1986
[1-7]:
M.
YA
BAKIROV,
R.
S.
MADATOV,
M.
YU
MUSTAFAEVA.
M.
ALLAKHVERDlEV, R B. GASYMOV
"Bi facial Solar Cell" Geliotehnika (Taskent) Coden GLOTTA Y, pp 64-65 1987
[1-8]: Le Quang NAM and M. ROOOT (Dir.)
"High Efficiency Solar Cells based on multicrystalline Solar" Thèse de Doctorat, Université de
Paris 07, 1992
[1-9]: Alain RICAUD
37
"Improvement of Silicon Solar Cells Efficiency With a Four Mirrors Configuration" Rapport,
FRA. DA, 1984
[1-10]: Daniel L. MElER., leong-Mo HWANG and Robel1 B. CAMPBELL
"The Effect of Doping Density and Injection Level on Minority-Carrier Liftime as Applied to
Bifacial Dendritic Web Silicon Solar Cells" I.E.E.E. Transactions
E.D.-35, nOl, pp. 70-79 lanuary 1988.
011
Electron Deviees, Vol.
[1-11]: Mamadou Lamine SOW
"Phénomène de Recombinaison dans la Photopile en Régime Statique et Transitoire" Thèse de
doctorat de 3ème Cyc1e, Ô.C.A.D., Dakar, Sénégal, Nov. Î 995.[1-12]: 1. FURLAN and S. AMON, Solid State Elect. Vol. 28 n° 12 (1985) 1241-3
[1-13]: MOHAMMAD S. N.
" An Alternative Method for the Performance Analysis of Silicon Solar Cel1s ", 1. Appl. Phys.
61 (2),767-772,1987.
[1-14]: Martin A. GREEN, Solar Cells, Ed. PRENTICE-HALL, U.S.A. page 96, (1982)
(1-15]: H. 1. HOVEL
Semiconductors and semimetals-Vol.ll, Solar Cells, p.50, Academie Press, 1975
[1-16]: Casimir MUSERUKA
"Effet de la longueur d'onde de l'excitation optique sur les phénomènes de recombinaison dans
une photopile en régime statique et transitoire" Thèse de doctorat de 3èmeJ:;ycle, U. C. A. O.,
Dakar, Sénégal, Mars 1995.
[1-17]: P. de VISSCHERE, Solid State Elect. 29(11), pp.1161-1165(l986)
[1-18]: R. GOPAL, R D. WlVEDI and S. K. SIRVATAVA Sol id State Electronics 26, pp.
1101-10 (1983)
[1-19]: M. A. GREEN Solar Cells Il, pp. 147-161,(1984)
[1-20]: S. R. DARIWAL Solid StateElectronics Vol. 24, nOlO, pp. 915-27 (198.1)
[1-21]: G. SIS~OKO Thèse de doctorat de 3 ème Cyële, p. 70 U.C.A.D. D(ikar-Sénégal( 1986)
38
[1-22]: G. SISSOKO, C. MUSERUKA, A. CORREA, 1. GAYE, A. L. NDIAYE
"Light Spectral Effect on Recombination Parameters of Silicon Solar Cell" Proc. 5th. World
Renewable Energy Congress, p. 1487, 15-21 June Denver (U.S.A.) 1996
. ;'
39
CHAPITRE II
ETUDE DE L'EMETTEUR D'UNE PHOTOPILE EN REGIME STATIQUE
INTRODUCTION
Ce chapitre est consacré à l'étude en régime statique du fonctionnement de l'emetteur
de la photopile qui est maintenue sous une excitation lumineuse blanche constante.
Dans cette étude, nous nous proposons d'extraire les paramètres macroscopiques ( courant,
tension, puissance, résistance de charge et capacité) de l'émetteur.
l~nf1uence
Nous an'alyserons
des recombinaisons des porteurs de charge aux interfaces
sur la puissance délivrée par l'émetteur de la photopile..
1 ETUDE DE LA DENSITE DES TROUS DANS L'EMETTEUR
Dans l'émetteur "dopé" de type n, les porteurs minoritaires sont des trous de charge q.
La densité des trous obéit à la loi de conservation des charges dont l'équation est donnée par:
a2 p n ( x ) - -~ PE
ap n (x)
-.
ax 2
Dp
ax
p (x)-p
n
n
0
L2
G(x)
=---
D
p
(II -1 )
P
Dans cette expression, Pn(x) désigne la densité des trous, ,u p est la mobilité des trous,
Dp est le coefficient de diffusion des trous dans l'émetteur, L p est la longueur de diffusion des
trous, pO est la concentration des trous à l'équilibre thermodynamique, et enfin G (x) est le
n
taux de génération des trous en fonction de la profondeur de l'émetteur [11-1 J.
1-1 Résolution de l'équation de continuité
En posant:
.1
1
[~E)2 + - 4
= -pD
L2 '
'
~
=
~ P E, et y
2· D
PpP
. l'équation (II-1) s'écrira comme suit:
,..--:-
=
~.1
2
40
.
a1 p ( x ) ,a p ( x)
n
-2p
n
2
ax
c7X
p (x)·_p
n
0
G(x)
n
=---
2
L
p
D
(1l-2)
P
La solution générale de l'équation (Il-2) se présente sous la torme suivante:
'J 3
x
x
x
' p (x)_po =e- P c e Y +c e- Y
+ L K.e
n
n
3
4
. i=l 1
'['
b.x
1
(1l-3)
avec
,
K.
a.
=
1
1
D
[b~-2P'b' __1)
pli
(1l-4)
L2
P.
La détermination des coefficients c3 et C4 se fait à l'aide des conditions aux limites qui sont:
1°) A la jonction ( en x = 0 ):
(1l-5)
SF p est la vitesse de recombinaison des trous à la jonction. C'est un paramètre
phénoménologique qui représente pour les trous, ce que SFn est pour les électrons.
AJors, il peut se décomposer en deux composantes comme suit:
SF = SFO + SF
2
p
P
(1l-6)
Dans cette relation, SF 2 est contrôlée la charge externe et SFO p caractérise les effets des états
d'interface à la jonction (côté émetteur) [II-2].
2°) Sur la face externe de l'émetteur ( en x
apn(x)\
ax
=
-dE)
SE
---.
x = -dE -
D
p
Pn (
dE
)
(1\-7)
41
Dans l'expression (II-7), SE désigne la vitesse de recombinaison des trous sur la face
externe de l'émetteur, Elle caractérise ies rerombinaisons des trous qui se déroulent à l'interface
émetteur/grilles collectrices,
11-2 Etude de la densité des porteurs
Dans ce paragraphe, nous faisons une étude en modélisation de la densité des trous
générés dans l'émetteur de la photopile pour diftërents points de fonctionnement.
Les paramètres de l'étude en modélisation sont:
Epaisseur de l'émetteur: dE = IJ1m,
Longueur de diffusion des trous: Lp :," 0.'1 J-lm,Taux de dopage de l'émetteùr: NE ;,':. 1020 cm- 3 ,
Mobilité des trous dans l'émetteur: IIp = 150cm 2/V.s,
Coefficient de diffusion D = 4cm2/s,
A l'aide de l'équation (II-2) munie de ses conditions aux limites, nous représentons sur la figure
(lI-l) les profils de densité des trous générés dans l'émetteur de la photopile en fonction de la
profondeur x pour différentes photopiles caractérisées par leur champ cristallin E (en V/cm).
1.3'1010
,.-------y------,----.------,------,
"
1>15
x(cm)
Figure (11-1 ):Densité des trous dans l'émetteur en fonction de sa profondeur x au voisinage du
circuit ouvert (SFp
=
Oc mis) et SE
=
103c!~/s pour différentes photopiles
La figure (II-I) représente la densité des trous en fonction de la profondeur de
l'émetteur au voisinage du circuit ouvert. Elle indique que le gradient des porteurs générés près
de la jonction est nul. Les porteurs situés dans cette région ne traversent donc pas la jonction.
Ils y sont stockés. Pour les porteur~ générés loin de la jonction, le gradient est négatif Ceux-ci
42
non plus ne traversent pas la jonction. Us peuvent se recombiner en volume ou à la face externe
de l'émetteur.
Cette figure montre également que la densité des trous dans l'émetteur n'est pas influencée par
le champ cristallin constant. Cependant, d'autres études [1I-3] ont montré l'influence du champ
variable sur les paramètres de l'émetteur.
Sur la figure (11-2) , nous représentons la densité des trous en fonction de la profondeur
au voisinage du court circuit pour diftèrentes photopiles caractérisées par leur champ cristallin
E (en V/cm):
1.5"10
10
1
1
1
1
-..
,
.f")
E
u
'-'
<Il
.....
1"10
10
-
f
:::
Q)
/
t
Er 0
0
0..
1
1
1
<Il
Q)
'"0
-<l)
1
-
5.109 1-'
/
.~
i
C
1
<Il
Q)
1
Cl
1
1
o
o
1
1
1
4·10 5
6·10 5
8"10 5
0.0001
x(cm)
Figure (11-2): Densité des trous dans l'émetteur en fonction de sa profondeur pour SFp = 10 7
cm/s et SE = l 03 cm/s pour différentes valeurs de E (V/cm)
La figure (1I-2) indique qu'au vOlsmage du court circuit .(pour lequel la vitesse de
recombinaison SF p des trous à la jonction est élevée), le profil de la densité des trous générés
dans l'émetteur présente trois régions:
- Une première région (proche de la jonction) où le gradient des porteurs est positif. Les trous
générés dans cette région traversent donc la jonction. Ils contribuent alors à la production du
photocourant.
~
Une deuxième région ou le gradient des porteurs est nul. Les porteurs qui se trouvent dans
cette région ne traversent pas la jonction.
- Et enfin, une troisième région (loin de la jonction) où le gradient des porteurs est négatif. Les
porteurs générés dans cette région aussi ne traversent pas la jonction. Ils se recombinent en
volume ou sur la face externe de l'émetteur.
Les porteurs de la deuxième et de la troisième région ne participent pas à la production du
photocourant. Pour ceux-ci, la photopile est placée en circuit ouvert. Comme les porteurs de la
. première région traversent la jonction: il se produit un phénomène semblable à. celui qui a été
43
observé dans la base à savoir que tout se passe comme si la photopile se réduisait d'une
quantité équivalente à la distance entre la jonction et la deuxième région. Ce phénomène est
alors assimilable à un élargissement de la zone de charge d'espace.
Sur la figure (II-3), nous présentons la densité des trous dans l'émetteur pour une
vitesse de recombinaison SE = 107cm/s et pour différentes photopiles caractérisées par leur
champ cristallin E (en V/cm).
•
r---M
1
E
u
-........
Vl
'-
Ë"')
J.IO IO
:J
o
Elo
Vl
(1)
;
0-
-(1)
......
.
/
(1)
t:
"'0
'.
1
E'~5
/
1
5.109
Vl
C
(1)
a
o
\
\
1
~
o
\
\
\
\
\
\
1
4"\0
1
5
6"\0
5
8·\0 5
0.000\
x(cm)
Figure (1I-3): Densité des trous dans l'émetteur en fonction de la profondeur x-de l'émetteur
pour SFp = 107 cm/s et SE=10 7 cm/s pour différentes photopiles.
La figure (II-3) montre que pour de grandes valeurs de la vitesse de recombinaison des
trous SE à la face externe de l'émetteur, la densité des porteurs générés près de la face externe
est faible. Les recombinaisons des porteurs dans cette partie de la photopile sont importantes.
C'est le phénomène qui se produit dans les surfaces de contact ohmique Tout se passe comme
si les contacts matériau semi-conducteur/grilles métalliques étaient des contacts métaVmétal.
II ETUDE DU PHOTOCOURANT DES TROUS
Ce paragraphe est une étude en modélisation du photocourant des trous en fonction de
la vitesse de recombinaison des trous à la jonction. Nous mettrons en évidence l'effet des états
d'interface de l'émetteur sur sa qualité.
Le courant délivré par l'émetteur de la photopile est dû au déplacement des trous qui traversent
la jonction.
La densité de photoc?,urant des trous est donnée par l'équation (11-8) [lIA]:
44
_ni
P 8x x=
8p
J
P
=q(-D
;
0:
+~ p (O)E)
P n
(11-8)
En réécrivant l'équation (11-8) à l'aide de la condition à la limite (Il-5), il vient que:
(Il-9)
A l'aide de l'équation (II-9), nous représentons sur la figure (11-4) les profils de densité
de photocourant délivré par l'émetteur en fonction de la vitesse de recombinaison des trous à la
jonction..p our di!férentes photopiles caractérisées par leuLchamp cristallin E (en V/cm),:
0.0003
if'·
-r--"
1
!
~
i
~
~
§
J
~
:k=15
.....
1
-
k=5
i=ü
u
0
:g
0...
1
2.635'10-7
0
3.5
17
log(SFp)
Figure (11-4): Densité de photocourant des trous en fonction de SFp pour SE
= 1Q3 crn/s pour
différentes photopiles.
La figure (11-4) montre que le photocourant de l'émetteur est faible aux fàibles valeurs
de la vitesse de recombinaison à la jonction des trous. 11 atteind sa valeur maximale aux
grandes valeurs de cette vitesse de recombinaison. En circuit ouvert, la photopile ne délivre pas
de courant tandis qu'en court circuit, le courant délivré par la photopile est maximal.
Cette figure montre également que la vitesse de recombinaison des trous aux interfaces
émetteur/contacts métalliques influencent peu le photocourant des trous. Ceci peut être lié aux
recombinaisons possibles des trous dans l'émetteur avant que ceux-ci ne traversent la jonction
.
.
pour participer à la production du courant.
Le champ cristallin constant n'influence pas le photocourant des trous car il intervient
dans Je-calcul du photocourant par l'intermédiaire de la densité des porteurs photogénérés.
Appliquons J'équation (11-6) représentant la décomposition de la vitesse de
. recombinaison des. trous en ses différentes composantes à l'équation (11-9) représentant la
45
densité de photo:courant des trous et· représentons la variation du photocourant des trous en
fonction de la vitesse de recombinaison SFp des trous à la jonction.
La figure (1I-5) présente les profils de densité de photocouram des trous en fonction de
SFp pour différentes photopiles caractérisées par les vitesses de recombinaison SFOp des
porteurs aux interfaces.
0.00032 , - - - - - - . -..-.t'·..-....-·- ..-...-....- ....-...-.. -...-...--'
...
;0
/
-
.t
,1
/1
(
~FOp= 1eo;1 J;'SFOp= 1e2
.....
..r·"
J
~FOp=
1eO
1
5.323°10-9 '----~.........- - - " - - - ' - - - - - - - - - - - - '
17
o
8.5
Iog(SFp)
Figure (11-5): Densité de photocourant des trous en fonction de SFp pour SE
=
l 03 cm/s et
pour différentes valeurs de SFOp (en cm/s)
La figure (Il-5) montre que la densité de photocourant des trous est faible en circuit
ouvert (faibles valeurs de la vitesse de recombinaison des trous à la jonction) et elle augmente
au fur et à mesure que cette vitesse de recombinaison augmente. La densité de photocourant
des trous atteind une valeur limite qui définit le courant de court circuit.
Elle est sensible aux variations de la vitesse de recombinaison SFOp des trous introduite par les
états d'interface.
En circuit ouvert, les recombinaisons liées aux interfaces masquent celles qui sont introduites
par la charge externe. POUf une photopile de bonne qualité, ces recombinaisons sont faibles,
tandis que pour une photopile de mauvaise qualité, ces recombinaisons sont importantes.
En court circuit, ces recombinaisons liées aux interfaces subsistent mais elles sont masquées
par celles qui sont introduites par la charge externe de la photopile. La qualité de la photopile
'est déterminée par ces phénomènes d'interface. Plus ils sont importants, plus la qualité de la
photopile est mauvaise.
III ETUDE DE LA PHOTOTENSION
46
La phototension de la photopile a pour origine le stockage des porteurs de charge
(électrons dans l'émetteur et trous dans la base). Ces gradients de concentration vont donner
naissance à un champ électrique, d'où une tension à lajonction (voir le paragraphe (1-3) ).
La tension délivrée par la photopile est calculée à partir des éléments de la base.
IV
ETUDE EN MODELISATION DE LA CARACTERISTIQUE COURANT-
TENSION DE L'EMETTEUR DE LA PHOTOPlLE
La caractéristique courant-tension de l'émetteur de la photopile peut être obtenue en
liant le photocourant (paragraphe (Il» et la phototension (paragraphe (lll» par le paramètre
phénoménologique commun qui est la vitesse d~ recombinaison à la jonêtion des trous.
Sur la figure (11-6), nous présentons les caractéristiques courant-tension obtenues en
modélisation pour différentes photopiles caractérisées par leur champ cristallin E (en Vlem).
0.00032 -
-
---_.
f=-····
..--.
~
~
<
'---'
-.gê
<n
1
E
tJ
0
p...
0
1
0
0.29
Ehototension (V)
0.717
Figure (11-6): Caractéristiques courant-tension dans l'émetteur pour SE = 10 3cm/s pour
différentes photopiles.
D'une façon générale, ces caractéristiques présentent la même allure que celles qui ont
été observées
da'15
la base de la photopile
No~s
observons alors que:
- Le photocourant des trous est maximal lorsque la tension délivrée par la photopile est
minimale. C'est le cas du fonctionnement en court circuit de l'émetteur de la photopile.
- Le photocourant des trous est minimal lorsque la tension délivrée par la photopile est
maximale. Dans ce cas, l'émetteur dela photopile fonctionne en circuit ouvert.
- Le champ n'influence pas de manière sensible la caractéristique courant-tension de l'émetteur
de la photopile. Ceci .déçoule du modèle du champ électrique contant.
47
V LE COURANT DE DIODE
A l'aide de l'équation (II-6), l'équation (1I-9) s'écrira:
J p =q[-(SFO p
+SF2)+~pE]Pn(O)
(ll-IO)
d'où
(II-II)
En posant:
'(Il-12)
où Je(SFp) est la fractiàn de photocourant des trous qui traverse la charge externe eUfe(SFp)
est celle qui est perdue dans les recombinaisons des porteurs aux interfaces.
L'expression de Jfe(SFp) est:
J fe
= -q .(SFO p '~p' E).P~[ eX{:T J-I]
(1I-13)
et celle de Je(SFp) est alors:
(II-14)
En circuit ouvert, nous faisons les hypothèses suivantes:
1°) Exp(Y/YT) » 1
et
D'après la première hypothèse, il vient que: J fe
~ .. q . (SFO p . ~p . E)· P~ [ex p( :T J] qUI
~
peut ètre décomposée en deux termes dont l'un ( ..q. SFO P P [ exp [
v~ ) - 1] ) est
proportionnel à un courant de diode sous obscurité et l'autre (-q. (S FO P - ~l P . E)· P~) est
proportionnel au courant qui traverserait la résistl1!lce shunt. Celui-ci est le courant de
saturation de l'émetteur de la photopile.
La diode et la résistance sont relatives à la vitesse de recombinaison SFOp à la jonction des
trous qui caractérise les états d'interface.
D'après la deuxième hypothèse: J p (SFP ) ~ J fe (SFp)' ce qui signifie que le photocourant se
réduit au courant de fuite.
48
En court circuit, nous posons: SFOp « (SF2 - ~pE). Dans ce cas, il vient que:
J p (SFP ) ~ Je (SFp ). Dans ce mode de fonctionnement, le photocourant est presque
entièrement délivré dans le circuit extérieur.
Dans un mode de fonctionnement intermédiaire, les phénomènes de recombinaison liées
aux interfaces et celles qui sont introduites par la résistance de charge externe coexistent.
La figure (Il-7) représente la vaiiatio~ du courant de diode en fonction de la tension de
différentes photopiles è~nictéri'sées pa~ leu'rch~p cristallin E (en V/cm).
-
...N
>
1.307"10 5
1
E
u
:<
1
1
1
1
1
'-'"
Q)
""0
0
""0
.-
6.535 " 10 6
i
'r-
c-
1
f
Q)
E = 1st
""0
1
......
i
@
l-.<
~
0
U
00"
1.934 " 10
17
1
0.006
E=J
E=Q/
0.362
G TI7
PhototensÎon (V)
Figure (1I-7): Courant de diode en fonction de la tension pour SfO p = 102 cmls pour
différentes photopiles.
Le courant de diode a été calculé à partir de la densité des porteurs photogénérés. Le
profil du courant de diode montre qu'il est très faible au voisinage du court circuit et il
augmente brutalement au voisinage du circuit ouvert.
Dans le fonctionnement en circuit ouvert de la photopile, les recombinaisons induites par les
états d'interface masquent celles qui sont introâuites par la charge externe ( Sf2 « SfOp ).
.
.
Par contre, il se produit le phénomène contraire en court circuit au cours duquel les
recombinaisons introduites par la charge externe masquent celles qui sont induites par les états
d'interfaces ( SF2 » SFOp ). Néanmoins, bien que les recombinaisons aux interfaces soient
masquées en court circuit par les recombinaisons introduites par la charge externe, elles
subsistent et ce sont elles qui déterminent la qualité de la photopile. La tension de circuit
49
ouvert d'une photopile de bonne qualité est élevée tandis qu'elle est faible pour une photopile
de mauvaise qualité. Il en est de même pour le courant de court circuit.
Enfin, l'influence du champ électrique cristallin n'a pas été observée sur le courant de
diode.
VI PUISSANCE DELIVREE PAR L'EMETTEUR
Ce paragraphe est une étude en modélisation de la puissance électrique produite par
l'émetteur de la photopile. Cette étude est effectuée en fonction du point de fonctionnement de
l'émetfeur. 'Elle tient compte des phénomènes de recombinaison dans les interfaces et du champ
. cristallin.
Nous ne tiendrons compte pour le calcul de la puissance électrique de l'émetteur que des pertes
causées par le paramètre phénoménologique SFOp.
La puissance électrique Pp(SFp) délivrée par l'émetteur de la photopile est donnée par
l'équation (II-15):
Pp(SFp)
=
(Jp(SFp)-Jfe(SFp)). V(SF n)
(II-15)
Nous représentons sur la figure (II-8) les variations de la puissance électrique de
l'émetteur en fonction de la vitesse de recombinaison des trous SFp à la jonction pour des
photopiles caractérisées par leur champ cristallin E (en V/cm).
0.0001
j
\,
\.
"-'.
."E=O
\
\ E=5
1
!
"
\
~
\
\E=15
'\,
\
f
-'
o
Figure (1I~8):
7.5
15
log(SFp)
Puissance délivrée par l'émetteur en fonction de SFp pour SFO p
différentes photopiles.
=
Ocmls pour
50
La figure (11-8) montre que d'une manière généraie, l'allure des courbes de puissance
délivrée par l'émetteur est la même que celle délivrée par la base de la photopile (Chapitre l,
paragraphe (III) )
La puissance électrique est faible au voisinage du circuit ouvert (faibles valeurs de la vitesse de
recombinaison des trous à la jonction) et du court circuit (grandes valeurs de la vitesse de
recombinaison des trous à la jonction). Elle atteind sa valeur maximale en un point de
fonctionnement intermédiaire.
La figure (11-8) montre également que la puissance électrique produite par l'émetteur est très
peu influencée par le champ cristallin constant.
Sur la figure (II-9), nous représentons la variation de la puissance électrique produite
par l'émetteur de la photopile en 'fonction cre la vitesse de recombinaison SFp des trous à la
jonction pour différentes valeurs de SFOp correspondant à différentes qualités de photopiles.
0.0Q044
("
,........
;
N
,
1
S
u
~
u
~
....
"-
':
/
f
-
Il)
\.'
'.
\
t
1
.?f9p~J'el
~
~
-
"'
..
\.
\
("
~
\.
\
t/
'9
\
. . ê.~Op=le4
1
0
8.5
0
17
log(SFp)
Figure(II-9): Puissance délivrée par l'émetteur en fonction de SFp pour différentes valeurs de
SFOp.
La figure (11-9) montre qu'aux faibles valeurs de la vitesse de recombinaison SF2 des
trous à la jonction ( circuit ouvert ), la qualité d'une photopile à l'autre diminue lorsque les
phénomènes de recombinaison aux interfaces deviennent de plus en plus importants. Dans ce
cas, la photopile fonctionne en circuit ouvert mais la tension de circuit ouvert est faible. Pour
des effets d'interface faibles dans une photopile fonctionnant en circuit ouvert, la tension de,
circuit ouvert sera importante. C'est le cas des photopiles de bonne qualité.
Aux grandes valeurs de SF2, les recombinaisons aux interfaces subsistent mais elles sont
masquées par l'action de la résistance de charge externe La photopile est alors placée en court
circuit. Le courant de court circuit sera d'autant plus important que la qualité de la photopile
est bonne.
51
La détermination du point :de puissance maximal se fait à l'aide de l'équation (1I-16):
(1I-16)
dont la résolution peut se faire de manière graphique.
VU LA RESISTANCE DE CHARGE nE L'EMETTEUR
Dans ce paragraphe, nous faisons une étude en modélisation de la résistance de ~harge
extèrne de la photopile. Nous étiJdierons le comportement des points de fonctio~Jnement de
l'émetteur de la photopile en fonction de la charge externe.
La résistance de charge externe de la photopile est en compétition avec la résistance shunt
propre de l'émetteur de la photopile qui introduit elle aussi une vitesse de recombinaison SFOp
des trous à la jonction.
La fraction de courant délivrée par l'émetteur qui traverse la résistance de charge externe
Rp(SFp) sous la tension V(SF n) conduit à l'expression (1I-17)
(1I-17)
Nous présentons sur la figure (II-IO) les variations de la vitesse de recombinaison des
trous à la jonction en fonction de la résistance de charge de l'émetteur de la photopile.
4
1
1
1
",-.....
0..
i-Ll
en
'--/
00 :2
........
0
-
"\
\
1
"
\.
"
'
.....
...,,-----------.
1
0
Û
1-10 8
-1··---..
:2 -10
8
J
3 -10
8
4 -,.- 8
!U
Résistance de charge (O.cm2)
Figure (ll-lO): Résistance de charge externe en fonction de Sfp.
La figure (1I-1 0) montre que les grandes valeurs de la résistance de charge externe de la
photopile introduisent de faibles vitesses de recombinaison des trous à la jonction. Dans ce cas,
la photopile fonctionne en circuit ouvert. Les faiblès valeurs de la résistance de charge externe
52
de la photopile introduisent de grandes vitesses de recombinaison des trous à la jonction. Ce
phénomène se produit lorsque la photopile fonctionne en court circuit.
VIIJ
ETUDE DE LA CAPACITE DE L'ELARGISSEMENT DE LA ZONE DE
CHARGE D'ESPACE
Dans ce paragraphe, nous faisons une étude en modélisation de la capacité de
l'élargissement de la zone de charge d'espace qui a lieu dans l'émetteur de la photopile.
L'étude de la densité des trous générés dans l'émetteur a montré que la zone de charge d'espace
s'élargit lorsque la vitesse de recombinaison des trous augmente. Pour les porteurs qui ne
participent pas à la production du"-photocburant, h pllOtopil'e semble être en circuit ouvert quel
que soit son point de fonctionnement. Ces porteurs stockés dans la 'photopile se comportent
comme des charges présentes sur les armatures d'un condensateur.
La capacité de l'élargissement de la zone de charge d'espace est calculée en ne tenant compte
des variations de la densité des porteurs photogénérés.
En désignant par C'p la capacité de l'élargissement de la zone de charge d'espace, nous avons:
C' = Qp
p
V
(11-18)
où Qp est la quantité de charges stockées à la jonction et V la tension qui y règne. Qp est
donnée par la relation Qp = q.Pn(O) où Pn(O) est la densité des trous à la jonction.
La figure (II-Il) reproduit la variation de la capacité de l'élargissement de la zone de
charge d'espace en fonction de la vitesse de recombinaison des trous à la jonction:
1.0"10-5 ,....,,---...-....- - - . . . . - - - , - - - - - - - ,
',\\
"-
~
\
'0
'~o.
9.00nO-6
l':l
u
\
~-
\
1
1
\•
1
\
\
\
6.411°10 - 9
L
\\
'-
',-
'--.. _
--'-_---....:~
o
log(S~)
_l
1
3.5
.
Figure (II-11): Capacité de l'élargissement de la zone de charge d'espace en fonction de SFp
pour SE
=
103 c mls
La figure (II-11) montre que la capacité de l'élargissement de la zone de charge
d'espace prend -de grandes valeurs au voisi!1age du circuit ouvert ( SFp - 0 ) et elle diminue
53
lorsque la vitesse de recombinaison des trous augmente (court circuit) Ceci a déjà été observé
dans la base.
Au voisinage du circuit ouvert, les porteurs ne traversent pas la jonction émetteur/base. Ils sont
stockés à la jonction.
En court circuit, les porteurs générés au niveau de la jonction la traversent et participent au
photocourant. Il n'y a donc plus stockage des charges générées à la jonction, d'où une faible
capacité pour l'élargissement de la zone de charge d'espace.
S4
CONCLUSlON
L'étude de l'émetteur de la photopile a montré que lorsque la résistance de charge
externe introduit une vitesse de recombinaison Sf2 des trous à la jonction faible comparée à la
vitesse de recombinaison SfOp induite par les états d'interface (SF2 «
SfOp), les
recombinaisons interfaciales masquent les recombinaisons introduites par la charge externe.
Dans le cas contraire ( Sf2 »
SfOp ), ce sont les recombinaisons introduites par la charge
externe qui masquent celles qui sont induites par les phénomènes liés aux états d'interface.
Lorsque la photopile fonctionne en court circuit, les vitesses de reêombinaison Sfp des
trous à la jonctiOIi sont élevées et la zone de charge d'espace s'élargit. La capacité de
l'élargissement de' la zone de charge d'espace est d'àut~mt plus faible que l'élargissement est
important.
L'étude a également montré que contrairement au phénomène observé dans la base de
la photopile, le champ cristallin constant n'influence pas de façon notable les paramètres de
macroscopiques de l'émetteur de la photopile.
L'étude de la puissance de l'émetteur a enfin montré que les recombinaisons aux
interfaces limitent les performances de la photopile. Du point de vue électrique, nous associons
au paramètre phénoménologique SfOp ( introduite par les états d'interface) une diode et une
résistance shunt.
55
BffiLIOGRAPHIE
[1I-I]: J. FURLAN and S AMON, Solid State Elect. Vol. 28 n°]2 (1985) 1241-3
[11-2]: Martin A. GREEN, Solar Cells, Ed. PRENTlCE-HAll, U.S.A. page 96, (1982)
[11-3]: S. SIVOTHTHAMAN, Le Qwang NAM, M. ROOOT, J. NUS, M. GHANNAM, J.
COPPYE, G. PALMERS, O. SARTl
"Optimization of Bulk and
Surface Recombination
Parameters
in
High
Efficiency
Polycristalline Solar Cells" Proc. 11th. European Photovoltaic Solar Energy Conf and
Exhibition 12-16 Oct. 1992[1I-4]: H. J. HOVEl
Semiconductors and semimetals- VoL 11 , Solar Cells, pp. 50, Academic Press, 1975
56
CHAPITRE III
ETUDE EN REGIME STATIQUE D'UNE PHOTOPILE ECLAIREE PAR SA FACE
ARRIERE
INTRODUCTION
La recherche de l'amélioration du rendement des photopiles a conduit à la fabrication de
photop.iles pouvant être éclairées par les deux faces. Ces photopiles, encore appelées
photopIles bJaciales [III-1..4 t prés-entent une face amère fôrtement "dopée" en atomes
.
-
d'impureté sur une faible épaisseur. Cette zone "surdopée" offre l'avantage de créer un champ
électrique qui a pour effet de renvoyer vers la jonction les charges photogénérées. L'une des
conséquences de l'existence de ce champ électrique est la diminution de la vitesse de
recombinaison SB des porteurs sur la face arrière.
Dans ce chapitre, nous étudions le fonctionnement en régime statique d'une photopile éclairée
par la face arrière.
Nous examinerons le comportement du photocourant et de la phototension de la photopile en
fonction des vitesses de recombinaison SF n et SB des porteurs de charge respectivement à la
jonction et sur la face arrière.
Nous étudierons les caractéristiques statiques 1-V de la photopile et l'influence de l'effet des
paramètres de l'excitation optique sur les vitesses de recombinaison SF n et SB.
1 ETUDE DE LA DENSITE DES PORTEURS DANS LA BASE
La densité mp(x) des porteurs photogénérés dans la base (de type p) éclairée par sa
face arrière est décrite par l'équation de continuité:
a2 m
Il E am (x)
_------'-p__ + _n_ . --:P__
ùx 2
On
ex
(x)
m (x)-m o
pp
L2
G'(x)
=---
n
0
°
(III-I)
n
Dans cette équation, mp est la concentration des électrons à l'équilibre, les paramètres
Ln, On. ~n ( déja dètinis dans l'equatlon (1-1) ) èièsignent respectivement la 'iongueur de
diffusion. le coefficient de diffusion. et la mobilité des électrons.
En maintenant l'origine des abscisses en x
=
0 ( jonction émetteurlbase ) et pour un
éclairement multispectral en face arrière, le taux de génération G(x) [III-5] s'écrira:
57
3
-b.(H-x)
G'(x)= l a.·e
1
.
1=
1
(1ll-2)
1
où ai, bi et H ont été définis dans le chapitre 1.
11-1 Résolution de l'équation de continuité
L'équation (IIl-I) est une équation différentielle du second ordre dont la solution
générale se présente sous la forme suivante:
m (x)-mo=e
p
P"
_I1 X (
1-'
-
y.x
-Y'X)- +
c e . -+c-e
5
. 6 -
3
l
.
=1
1
K.e
-b.(H-x)
1
1
(1ll-3)
où les paramètres ~, y, et Ki ont déjà été déterminés dans le chapitre 1.
La détermination des constantes cS et c6 se fait à l'aide des conditions aux limites (1-6) et (1-8).
11-2 Etude de la densité des porteurs
Nous représentons la modélisation du profil de la densité des porteurs en fonction de la
profondeur de la base de la photopile.
L'influence du champ électrique cristallin et de la vitesse de recombinaison SF n des porteurs de
charge à la jonction sur la densité des porteurs sera mise en évidence_
A l'aide de l'équation (lII-3) munie des conditions aux limites, nous présentons sur la figure
(III-I) les profils de densité des porteurs en fonction de la profondeur x de la base pour
différentes valeurs du champ cristallin E (en V Icm) correspondant à différentes photopiles_
8°10 13 , . - - - - - - - - - , - - - - - - - - - - ,
E = l;î
Ul
<1)
/
-0
~
!
·-.:.c.-. :.c· ~-~- -~ ~= = :- l ._-_-_-_- - _·~_~_f_"_/-_~_-~_(_) _1
,w" l.:.c.-. :.co
~-....
~
--
<{).Oy
x(cm)
Figure (IJI-I): Densité des porteurs dans la base pour SF n = Ocm/s et SB = 102 cm/s en
fonction de la profo~deur pour différentes photopiles (Ln = 501J.m)
58
La figure (III -1) montre que la densité des porteurs de charge générés dans la base de
la photopile fonctionnant en circuit ouvert est plus faible au niveau de la jonction que sur la
face arrière. Dans ce mode de fonctionnement, le gradient des porteurs à la jonction est nul.
Les porteurs créés ne traversent pas la jonction.
La génération des porteurs de charge est plus importante sur la face arrière qu'à la jonction de
la photopile éclairée par la face arrière.
La figure (IIl-l) montre également que pour différentes photopiles caractérisées par leur
champ cristallin accélérateur, la densité des porteurs photogénérés est plus importante lorsque
le champ cristallin est important.
Sur -la figure (1Il-2), noûs présentons les profils de densité des porteurs pour différentes
photopiles caractérisées par leur champ cristallin E (en V Icm) en fonctionnement au voisinage
du court circuit.
s·.ol3 , - - - - - - - - - - - - , 1 - - - - - - - - - - - - - ,
/
.r
/
/
/
/
/
-
-" ..
- ' r ---
o
~
x(cm)
Figure (1ll-2): Densité des porteurs dans la base pour SF n = 106cm/ s et SB '''' 102 cm/s en
fonction de la profondeur pour différentes photopiles
La figure (1ll-2) montre que pour un point de fonctionnement voisin du court circuit
(grandes valeurs de SF n), le gradient des porteurs à la jonction est supérieur à zéro. Ainsi, la
'"itesse SFn âes porleurs est suffisamment elevee pour leur permettre de traverser la jonction.
Elle montre également une forte génération de porteurs à la face arrière. Ce phénomène a déjà
été observé dans la base de la photopile fonctionnant au voisinage du circuit ouvert (Figure(lIl1».
La figure (IIl-2) indique aussi que pour différentes photopiles caractérisées par leur champ
cristallin et fonctionnant en court circuit, la densité des porteurs ph~togénérés est importante
lorsque le champ cristallin est important.
59
Il ETUDE DU COURANT DANS L'\ BASE
Dans ce paragraphe, nous faisons une étude en modélisation de la densité de
photocourant délivrée par la base de la photopile éclairée par la face arrière.
Nous étudierons l'influence des vitesses de recombinaison Sf n et SB des porteurs de charge
respectivement à la jonction et sur la face arrière de la base de la photopile sur la densité de
courant. L'influence des phénomènes de recombinaison liés aux états des interfaces sera
également mise en évidence.
A partir de la densité des porteurs, la densité de courant est donnée par [1II-6]:
ant
J' =q D
n
[
n
(x)
P
OX
.
]
l'
-0+J..l E·m (0)
xn
p
(IlI-4)
aO) Photocourant en fonction de SFn
A l'aide de l'équation (1-6) du chapitre 1 ( dans laquelle la densité des porteurs est
désignée par mp(x) ), l'équation (IlI-4) devient:
J' :::q(SF +J..l E)m (0)
n
n
n
p
(1ll-5)
A partir de l'expression de la densité de courant, nous produisons les courbes de
variation du photocourant en fonction de la vitesse de recombinaison Sf n des porteurs à la
jonction à travers la figure (1Il-3) pour différentes valeurs du champ cristallin E (en Vlem)
correspondant à différentes qualités de photopiles.
60
0.02
i
1
1
,1
-
IL ~ 15
0.01 -
VJ
Q)
i
'"0
§....
g
/
/
u
i
1
.8
~
E~S
/
0..
6.77?10 8 '------='-/_-'-'-_""'-------'-I_ _
.L_·~_".O_-_... -_-_-_=__--------'-
log(Sl'n)
'Ü-
figure (111-3): Densité de photocourant dans la base en fonction de Sf n pour SB
pour différentes photopiles.
=
102cmls
La figure (IIl-3) montre que pour les faibles valeurs de la vitesse de recombinaison Sf n
à la jonction des porteurs ( circuit ouvert ), la densité de photocourant est faible. Lorsque la
vitesse Sf n augmente, la densité de photocourant augmente jusqu'à une valeur maximale qui
définit le courant de court circuit.
Pour différentes qualités de photopiles, la densité de photocourant est d'autant plus importante
que le champ cristallin ( nous avons fait l'hypothèse d'un champ cristallin accélérateur
d'électrons) est important pour un point de fonctionnement donné.
Sur la figure (III-4), nous représentons le profil des densités de photocourant des
électrons pour différentes qualités de photopiles ayant différentes valeurs de la vitesse de
recombinaison SfOn des électrons à la jonction introduites par les états d'interface [III-7].
.
0.001
··t······
.-.......
.
.
,i
,',
;,
'1
.
::iFOn= 1e:4
.... - ....
1
' .:;
~
1
i
-
~5
(
.
t
u
o
.2
f
0..
~.031'10
-
.,
.
,
1
_1
r
f:>FOn=uf
_ /,/ SFOn=O
1--_---=..'
oC·
1
-'---
-'
log(~n)
figur~ (IlIA): Densité de photocourant en fonction de Sf n pour SB = 102cmls et pour
différentes valeurs de SfO n
61
La figure (1II-4) montre que pour de faibles valeurs de la vitesse de recombinaison Sf n
des porteurs de charge à la jonction (colTespondant au fonctionnement en circuit ouvel1 de la
photopile), le photocourant délivrée par la photopile est faible. Il augmente au fur et à mesure
que SFO n augmente. SFO n caractérise les fuites qui ont lieu dans les états d'interface. Cette
figure montre alors que l'influence des effets d'interface sur le photocourant est importante
pour les faibles valeurs de la vitesse de recombinaison à la jonction des porteurs imposée par la
charge externe.
Ces effets d'interface sont masqués au voisinage du court circuit. En effet, dans ce mode de
fonctionnement, la vitesse de recombinaison SF 1 à la jonction des porteurs introduite par la
résistance de charge externe est très élevée par rapport à SFO n ( SF 1 » SFO n ). En court
circuit, la vitesse-de recombinaison à'"la jonction des pdrteurs se réduit à celle définie par la
charge externe (SFn ~ SF1)·
Les figures (1II-1) et (III-2) représentant les profils de densité des porteurs ont montré
une forte génération de porteurs à la face arrière de la base. Les figures (1II-3) et (III-4)
montrent que la densité de photocourant est constante quelle que soit SF n au voisinage du
court circuit.
Dans ce paragraphe, nous étudierons l'influence du rayonnement sur la vitesse de
recombinaison SB à la face arrière des porteurs.
En court circuit, nous écrivons:
al'
__n_=
aSFn
°
(1II-6)
Cette équation aboutit à une équation du second degré à coefficients constants en SB qui est:
2
A SB + B SB + C =
°
(111-7)
où nous avons:
1[
Sf
2 + L . -n. th [H
[H '] . (1 - exp( - b· . H). [SF
n D
L
A == - . 1+ L .- n. th D2
n D
L
n
n
n,
J
n
n
J]]
011-8)
62
1
B=-·
On
(1l1-9)
et
c=
(11l-IO)
Les racines SBI et SB2 de l'équation (II1-7) sont données par:
-B--Ji.
SB I =-2-A-
(III-11)
et
-B+-Ji.
SB 2 =-2-A-
où
~
(11I-12)
est le discriminant ( positif) de l'équation (l1l-7)
Les racines de l'équation (II J- 7) sont des fonctions des paramètres H, Ln On et des termes de
génération. En tàisam la sommation sur tous les termes de la seriè en i (prenant en compte
toutes les radiations composant le spectre du rayonnement), les vitesses SB 1 et SB2
constituent les vitesses de recombinaison résultantes des porteurs à la face arrière de la base.
De ces deux racines, SB2 > 0 et SB l < 0
Physiquement, une vitesse de recombinaison négative correspond à un gradient positif en face
arrière pour la densité des porteurs. Le profil de la densité des porteu.rs est analogue à celui qui
est produit par une injection électrique de porteurs. Une vitesse de recombinaison positive
63
correspond à fun gradient négatif en face arrière. Le profil de la densité des porteurs est
semblable à celui qui est produit par une génération optique de porteurs.
Ainsi, la vitesse de recombinaison des porteurs à la face arrière de la base des porteurs est la
racine SB2. Elle tire son origine de l'effet optique résultant du rayonnement.
La figure (III-5) reproduit la variation de la vitesse de recombinaison SB2 des porteurs
à la face arrière en fonction de l'épaisseur de la base.
1. 724 "10
5
1
r-..
li)
Êu
'--'
01
CD 8.619 10
4
Cl
lfJ
dl
7
-
1
!
li)
li)
i
dl
......
1
>
l,
a
.j = 1 .i.==-2 _i=:= 3 __ .
-- .-- -- --- --
-.
1
0
0.015
0.03
H(cm)
Figure (III-5): Variation de la vitesse de recombinaison SB2 en fonction de l'épaisseur de la
base pour SF n = 10 7cm/s
La figure (III-5) montre que la vitesse de recombinaison des porteurs à la face arrière
est élevée pour des photopiles dont la base est de très faible épaisseur. Elle décroît lorsque
l'épaisseur de la base augmente et atteind une valeur limite.
L'épaisseur moyenne de la base d'une photopile au silicium étant de 200J.-lm, nous présentons
dans les tableaux (lII-l), (III-2) et (HI-3) les vitesses de recombinaison calculées pour
différentes qualités de photopiles.
Tableau (lII-l ): Calcul de la vitesse de génération-recombinaison SB2 pour différentes
photopiles (Ln = 25J.-lm, On = 26cm 2/s)
H(~m)
SB2(Cm/s)
150
3.12 104
200
3.12 10 4
250
3.12 104
3.12 10 4
300
64
Tableau crll-2): Calcul de la vitesse de génération-recombinaison SB2 pour différentes
photopiles (l-n = 4S~lm, On = 26cm 2/s)
1.738 104
1.734 104
ISO
200
1. 733 104
1.733 104
2S0
300
Tableau (Il1-3I: Calcul·de la vitesse.de génération-recombinaison SB2 pour différentes
photopiles (Ln = 7Sllm, On = 26cm 2/s)
H(llm)
200
1.079 104
1.0S0 104
2S0
1.043 104 .
300
1.041 104
ISO
Remarques: Les tableaux (lII-I), (I11-2) et (III-3) montrent que:
Pour des photopiles au silicium de même dopage (0 est constant) et d'épaisseurs différentes
(IS0Ilm < H < 300llm), la vitesse de recombinaison SB2 est constante.
Pour des photopiles de même dopage
CD
est constant) et de recombinaisons en volume
différentes (Ln variable), la vitesse de recombinaison SB2 des porteurs de charge en face
arrière varie. Lorsque Ln augmente, SB2 diminue. De faibles recombinaisons en volume
produisent de fortes recombinaisons en surface.
bO) Photocourant en fonction de SB
Dans l'équation (III-S), la densité des porteurs mp(O) dépend de la vitesse de
recombinaison SB des porteurs à la face arrière de la base.
Nous produisons la variation du photocoUfant en fC!1ction de SB 2 !2. 5~ure (IIJ-6) ,peur une
photopile dont la base est quasi-neutre (E
=
OV/cm).
65
---.'-
0.00\
1
\ '.
\
\
\
\,
\
\.
-
-
\
'.
"
\
~',~
_
_
-._.-
--
1
o
j
00·
"10·
log(SB)
Figure (11I-6): Photocourant en fonction de SB pour SF n = 10 5cmls.
La figure (III -6) montre que pour les faibles valeurs de la vitesse de recombinaison SB,
le photocourant est constant et prend une valeur élevée: Cette zone correspond aux photopiles
B.S.F.
Aux grandes valeurs de SB, le photocourant est également constant mais il prend une valeur
plus faible. Cette zone correspond aux photopiles ohmiques.
Dans les domaines où le photocourant en fonction de SB est constant, nous pouvons poser
l'équation:
al'
__
n =0
(III-13)
aSB
La résolution de l'équation (111-13) mène à l'équation de variables SF n:
p. SF 2 -\- Q. SF + R = 0
n
n
(1Il-14)
L'équation (111-14) est une équation du second degré en SFn à coefficients constants tels que:
67
En posant .1 comme étant le discriminant de l'équation (III - 14), les deux solutions possibles
(car .1 dépend des paramètres H, Ln, On, SB et des termes de génération) de cette équation
s'écrivent:
--Q - li.
SF'nl _. ---.. -----~
(1ll-18)
2·P
et
(1II-19)
Les expressions (Ill-18) et (Ill-19) ne dépendent pas du point de fonctionnement de la
photopil~.
Elles dépendent seulement qe H, Ln, On, SB et des termes de génération.
La -solution positive (SF n2) correspond à la vitesse de recombinaison produite par une
génération optique de porteurs tandis que la solution négative (SF n 1) correspond à la vitesse
de recombinaison produite par une injection électrique de porteurs. La source d'excitation étanl
lumineuse, la vitesse de recombinaison des porteurs est la vitesse SF n2.
Cette vitesse de recombinaison a pour origine le couplage optique entre l'émetteur et la base de
la photopile.
Sur la figure (III-7), nous produisons la variation de la vitesse de recombinaison SFn2
des porteurs due au couplage optique en fonction de l'épaisseur de la base.
2241.214
N
Cl
~
1133.696
20.118
lÛJ
H (cm)
lÛ .03J
Figure (1lI-7): Variation de SF n2 en fonction de l'épaisseur H de la base
La figure (Ill-7) montre que pour des photopiles au silicium d'épaisseurs différente:;
(150~m
<H<
300~lm),
la vitesse de recombinaison Sfn2 des porteurs de charge à la jonction
due à l'effet optique tend vers une valeur limite au-delà de laquelle les variations de la base
n'influencent pas SF n2. Ceci signifie que les phénomènes de recombinaison liés à l'excitation
optique sont les mêmes à la jonction de la photopile.
111 ETUDE DE LA PHOTOTENSION
68
A l'aide de l'équation de Boltzmèmn, la tension Va délivrée par la photopile éclairée par
la face arrière de la base s'exprime par:
,
r
i'
Hi
t->
(0)
j
V ::::. \1 'T .• n 1,-------- +- 1
a
J.
1
0
1
m
L
(III-20)
P
Nous représentons sur la figure (IlI-8) la variation de la tension en fonction de la
vitesse de recombinaison Sf n des électrons à la jonction pour des photopiles de différents
champs cristallins_
:>
0.4
'.
<::
o
oc;;
<::
<J
"0
o
..r::
0..
(>.2
o
<{Y
log(SFn)
Ftgilre (IlI-8): Tension délivrée par la photopile éclairée par l'arrière en fonction de SF n pour
SB 104cm/s et pour différentes valeurs du champ E (V/cm)
==0
La figure (1Il-8) montre que la tension délivrée par la photopile éclairée par la face
arrière de la base est maximale aux tàibles valeurs de la vitesse de recombinaison SF n à la
jonction des porteurs. Cette valeur cOlTespc1nd à la tension de circuit ouvert. Aux grandes
valeurs de SFn, la photopile ne délivre pas de tension. Elle fonctionne en court circuit.
La figure (IIl-8) montre également que pour différentes photopiles, la tension délivrée par
chacune d'elles est d'autant plus importante que le champ cristallin ( accélérateur d'électrons)
est important.
En tenant compte des effets des états d'interface, nous reproduisons sur la figure (1II-9) la
variation de la tension en fonction de la vitesse de recombinaison à la jonction des porteurs
pour différentes valeurs de SfO n correspondant à différentes qualités de photopiles.
69
-
,
"
'.
'-.
o
15
15
log(Sfn)
Figure (1lI-9): 1=ension délivrée par la photopile éclairée par l'arrière en fonction de Sf n pour
différentes valeurs de SFO n (cm/s)
La figure (IIl-9) montre l'influence des états d'interface sur la tension de circuit ouvert.
Lorsque les effets des états d'interface deviennent de plus en plus importants d'une photopile à
l'autre ( grandes valeurs de SFO n ), la tension de circuit ouvert diminue.
Nous présentons sur le tableau (IIIA) les valeurs calculées des tensions de circuit ouvert pour
trois photopiles caractérisées par les états d'interface.
Tableau (IlIA): Tensions de circuit ouvert calculées pour trois photopiles caractérisées par les
états d'interface
Photopiles
SFO n
V eo
(crn/s)
(mY)
504
B
10 2
104
475
C
105
423
A
Le tableau (III-4) montre une variation considérable de la tension de circuit ouvert
calCulée pour les trois photopiles considérées. La tension de circuit ouvert baisse lorsque les
états d'interface ( caractérises par ia vitesse de recombinaison SFO n ) deviennent importants.
La qualité de la photopile est influencée par les états d'interface: Plus les
recombinaisons aux interfaces d'une photopile sont importantes, plus elle est de mauvaise
qualité.
70
IV CARACTERISTIQUES COURANT-TENSION DE LA PHOTOPILE
Dans ce paragraphe, nous faisons une étude en modélisation de la caractéristique 1-V
.de la photopile éclairée par la face arrière. Elle est obtenue en reliant le courant à la tension de
la photopile pour chaque point de fonctionnement caractérisé par la vitesse de recombinaison
SF n ·
La figure (1II-10) représente les caractéristiques courant-tension de différentes photopiles
caractérisées par le champ cristallin E (en V/cm)
0.022
E~ 1~__
..........
1
-_._ ... _-.. __
..... -
,~
N
E
u
:;:
\
\
1
\
\
\
\
'-'
en
c::
0
.....
U
Q)
~
<Il
Q)
0.011
I-
f-
\
\
\
\
'"Cl
§.....
::l
0
U
0
0
...c::
p..,
.
..E .':~.5 ...
E-=-lL-
-8
---t-
6.776 10
.0000449373'
Phototensioll (V)
.0628167,
Figure (III-I 0): Caractéristiques courant-tension de trois photopiles éclairées par la face arrière
pour SB = 102 crnls
La figure (III-lO) montre que-le courant de court circuit et la tension de circuit ouvert
sont très peu sensibles aux faibles variations de la vitesse de recombinaison des électrons sur la
face arrière de la base. Elles montrent également que pour différentes photopiles, les valeurs de
courant de court circuit et de tension de circuit ouvert sont d'autant plus importantes que le
champ cristallin ( accélérateur d'électrons) est important
V ETUDE DU COURANT DE DIODE Otl COURANT D'OBSCURITE
En tenant compte des effets des états d'interface, l'équation (lIl-S) s'écrit:
(Bl-21)
L'expression (III-21). peut se
décor..npo~erde
la manière suivante:
71
l'n =l'f+J\
(III-22)
où
(111-23)
et
J'f est la fraction de photocourant relative aux phénomenes d'interface. Ils caractérisent les
pertes au niveau des interfaces.
J't est la fraction du photocourant qui traverse la charge externe.
Lorsque la photopile· fonctionne en circuit ouvert, nous faisons les hypothèses
suivantes:
]1
découle de la premiére hypothèse que J' f (SFn )
~ q .(SFO n + Il n . E)· m~ [ex p [ ~~ )] et
de la seconde que J'n (SF n ) ~ J'f (SF n )·
Le photocourant se réduit dans ce cas au coural!! de fuite qui peut se décomposer en un
courant de diode J'd sous obscurité et en un courant l'r qui traverserait la résistance shunt de la
photopile dont les expressions sont
(1Il-25)
et
J' r =q·(SFO n +"~/l ·E)·m op
(111-26)
Lorsque la photopile fonctionne en court circuit, l'hypothèse SF J » (SFO n + ~nE)
'conduit à J' n (S Fn ) : : : J' t (SFn ). Dans ce mode de fonctionnement alors, le photocourant est
presque entièrement délivré dans le circuit extérieur.
Dans un mode de fonctionnement intermédiaire, les phénomènes liés aux états
d'interfaces et ceux liés à la charge externe coexistent.
72
La figure (Ill-Il) représente la variation du courant de diode en fonction de la tension
délivrée par la photopile.
(J (JO 1
,
~
N
1
E
1
~
-.......-
1
u
1
1
'(1)
1
·ë
1
:::l
u
1
VJ
0
.D
1
1
!
0
=0
§....
1
E .=
:::l
0
E~·
U
.
3.916 \0
/
\i5
5
12
0.\07
0.367
0.627
Phototension (V)
Figure (III-Il): Courant de diode en fonction de la tension pour SB = 10 2 cm/s et SFO n
102 cm/s et pour différentes valeurs du champ E (V/cm)
=
Le courant de diode sous obscurité représenté à la figure (Ill-Il) est calculé à partir de
la densité des porteurs photogénérés dans la photopile
Cette figure montre que le courant de diode sous obscurité correspondant au courant de fuite
de la photopile sous illumination est négligeable au voisinage du court circuit (faibles valeurs
de la tension délivrée par la photopile). Dans ce mode de fonctionnement, les recombinaisons
liées aux interfaces sont masquées par les recombinaisons liées à la charge externe de la
photopile. Cependant, les phénomènes d'interface subsistent.
Au voisinage du circuit ouvert (grandes valeurs de la tension délivrée par la photopile), le
courant de diode devient important. En circuit ouvel1, les phénomènes de recombinaison liés
aux interfaces masquent à leur tour les recombinaisons liées à la charge externe Les fuites sont
importantes dans ce cas.
Enfin, tout comme dans le cas de l'éclairement de la photopile par la face avant de
l'émetteur, l'influence du champ sur le courant de diode n'est pas remarquable dans Je cas de la
photopile éclairée par la face arrière de la base.
VI PUISSANCE DELIVREE PAR LA BASE DE LA PHOTOPILE
Dans ce paragraphe, nous faisons une étude en modélisation de la puissance électrique
délivrée par la base de la photopile. Nous mettrons en évidence l'influence du champ cristallin
accélérateur d'électrons et des phénomènes liés aux états d'interface sur la puissance de la
photopile.
73
Nous ne tiendrons compte, pour le calcul de la puissance électrique de la photopile, que des
pertes liées aux recombinaisons aux interfaces. Avec cette hypothèse, la puissance P'(SF n) de
la photopile s'exprime par:
P'(SF )=J' (Sf) \1 (SF )
t
n
a
n
n
(111-27)
Nous présentons sur la figure (Ill-12) la puissance électrique de différentes photopiles
caractérisées par leur champ cristallin E (en Y/cm) en fonction de la vitesse de recombinaison
des électrons à la jonction.
OJlIl
i
1
i
<l)
u
§
O.OO(i
i
CIl
CIl
1
1
1
:::l
0..
1
1
\
/
\
!
/
5.6.12.10- 9 '----"---"-~
<{).>
log(SFn)
Figure (1II-12): Puissance de trois photopiles caractérisées par leur champ cristallin E (Y/cm)
en fonction de SF n pour SB = Ocrnls.
La figure (III-12) montre que la puissance des photopiles est faible en circuit ouvert et
en court circuit. Elle atteind une valeur maximale en un point de fonctionnement intermédiaire.
La puissance délivrée par une photopile est d'autant plus importante que le champ cristallin (
accélérateur d'électrons) est important.
En tenant compte des effets d'interface, nous représentons sur la figure (1 JI -13) la puissance
délivrée par deux photopiles de différentes qualités caractérisées par les recombinaisons liées
aux états d'interface pour différents points de fonctionnement:
74
1
0.000::113
g;
)
,
,
1
,
,
1
,
,
1
:
,
,
,
,
,
-.1
o
,
,
'--_--'
1.5
15
log(SFn)
Figure (III-13): Puissance délivrée
p~r
deux photopiles de différentes qualités en fonction de
SF n pour SB == 10 2cmls
La figure (III-13) montre que la puissance maximale de la photopile diminue lorsque les
recombinaisons aux interfaces deviennent importantes. Les pertes dans les interfaces
contribuent à diminuer la puissance électrique que délivre la photopile.
Nous analysons dans le tableau (I1I-5) l'influence des recombinaisons aux interfaces sur la
puissance maximale des photopiles.
Tableau (III-5): Influence des recombinaisons aux interfaces sur la puissance maximale
Photopiles
SFO n
P max
(mW/cm 2)
C
(cmls)
102
0
104
0.199
0213
Le tableau (III-5) montre que pour de fortes recombinaisons aux interfaces, la
puissance maximale de la photopile diminue. C'est le phénomène qui se déroule dans les
photopiles de mauvaise qualité.
Le~
recombinaisons aux interfaces déterminent la qualité de la photopile
VIl RESISTANCE DE CHARGE DE LA PHOTOPILE
Nous étudions en modélisation la résistance de charge externe de la photopile. La
fraction de photocourant qui traverse la résistance de charge externe de la photopile est l't (
équation (III-24) ) Elle sera exprimée alors par:
75
V (SF )
R'(SF )=~_n~.
n
l' (SF \
t
nJ
(1ll-28)
La figure (1ll-14) montre les points de fonctionnement de la photopile pour différentes
valeurs de sa charge externe:
0.4 .95387t+006'
Résistance de charge (O. cm2)
Figure (IIl-14): Points de fonctionnement de la photopile pour différentes valeurs de la charge
externe.
La figure (IIl-14) montre que pour de grandes valeurs de la charge externe, la vitesse
de recombinaison SFn des porteurs de charge à la jonction est faible. La photopile fonctionne
en circuit ouvert.
Pour de faibles valeurs de la charge externe, la vitesse de recombinaison SFn des porteurs à la
jonction est élevée. La photopile fonctionne en court circuit.
UX
ETUDE DE LA CAPACITE DE L'E',LARGiSSEMENT DE LA ZONE DE
CHARGE D'ESPACE
Lorsque la photopile est éclairée par la face arrière de la base et qu'elle fonctionne en
circuit ouvert, les porteurs générés ne traversent pas la jonction. lis restent dans la base où ils
peuvent se recombiner. De même, dans le fonctionnement en court circuit de la photopile,
certains porteurs ne traversent pas la jonction. Pour ceux-ci, la photopile est en circuit ouvert.
Pour les porteurs se trouvant dans la région de la photopile où ils ne traversent pas la jonction,
la photopile semble être réduite à cette région. D'où un phénomène qui ressemble à un
élargissement de la jonction.
76
En ne tenant compte que des modifications de la densité des porteurs dans la base, nous
effectuons un calcul en modélisation de la capacité C' de l'élargissement de cette jonction par la
relation suivante:
C' = V'/Q'
(1ll-29)
où Q' = q. mp(O)
La figure 011-15) représente la variation de la capacité de l'élargissement de la zone de
charge d'espace en fonction de la vitesse de recombinaison SFn des porteurs à la jonction.
"
-7
1.4 JO'
==--.
,--
---,
1
.',
\
\,
'.
\
\
\\
.'.
\
\.
'\
1.336"10 -}O
1
<--.~.
'--------'----=---'
'Ü,
log(Sfn)
Figure (111-15): Capacité de l'élargissement de la zone de charge d'espace en fonction de SF n
pour SB = 10 3cm/s
La figure (111-15) montre qu'aux grandes valeurs de la vitesse de recombinaison des
porteurs à la jonction ( voisinage du court circuit ), la capacité de l'élargissement de la zone de
charge d'espace est nulle ( C'
~
0 ) Dans ce mode de fonctionnement, l'élargissement de la
zone de charge d'espace est important.
Aux faibles valeurs de la vitesse de recombinaison des porteurs à la jonction ( voisinage du
circuit ouvert ), la capacité de l'élargissement de la zone de charge d'espace est élevée. En
circuit ouvert, l'élargissement de la zone de charge d'espace est faible.
CONCLUSION
Au cours de l'étude du fonctionnement en régime statique d'une photopile éclairée par
la face arrière de la base, nous avons pu observer l'effet du rayonnement sur les vitesses de
recombinaison SF n et SB des porteurs respectivement à la jonction et sur la face arrière.
La vitesse SF n ( qui se découplait auparavant en deux composantes dont l'une est liée à la
charge ext~me de la photopile et l'autre relative aux effets d'interface ) peut contenir une
77
troisième une composante SFopt liée au couplage optique entre l'émetteur et la base. Ainsi, il
vient que: SF n = SFû n + SF l + SFopt ·
La vitesse SB contient une composante relative à J'effet optique SB opt en plus de la
composante SBint liée aux effets d'interface à la face arrière Ainsi: SB = SBint + SB opt
Nous avons également pu étudier les effets d'interface sur la qualité de la photopile. Nous
avons pu remarquer que la qualité de la photopile se détériore lorsque les phénomènes
d'interface deviennent importants. Ces phénomènes de recombinaison aux interfaces
introduisent une vitesse de recombinaison SFû des porteurs à la jonction qui causent une
diminution de la tension de circuit ouvert et augmentent les fuites dans la photopile.
78
BIBLIOGRAPHIE
[III-l]: A. CUEVAS, A. LUQUE, 1. EGUREN, 1. DEL ALAMO
"High Efficiency Bifacial Back Surfaee Field Solar Cells" Solar Cells, Vol. 3, n04, pp 337-340
1981
[I1I-2]: 1. EGUREN, 1. DEL ALAMO, A. LUQUE
"Optimisation of p+ Doping Level of n+ p p+ bifacial BS.F. Olar Cells By Ion Implantation"
Electron. Letters Vol. 16, n° 16, pp.633-634, 1980
. [111-3]: G. C. JAIN: S. N. SINGH"and R. KOTNALA
.
,
"Diffusion Length Determination ln n+ p p+ Structure Based Silicon Solar Cells From the
Intensity Dependenee of the Short Circuit CUITent for Illumination trom the p+ Side" Solar
Cells 8 239-48, 1983
[III-4]:
M.
YA
BAKIROV,
R.
S.
MADATOV,
M.
YU
MUSTAFAEVA.
M.
ALLAKHVERDIEV, R. B. GASYMOV
"Bifacial Solar Cell" Geliotehnika. (Taskent) Coden GLOTTAY, pp 64-65 1987
[111-5]: Daniel L. MEIER, leong-Mo HWANG and Robert B CAMPBELL
"The Effect of Doping Density and Injection Level on Minority-Carrier Liftime as Applied to
Bifacial Dendritic Web Silicon Solar Cells" I.E.E.E. Transactions on Electron Deviees, Vol.
E.D.-35, nO l, pp 70-79 January 1988.
[I1I-6]: H. 1. HOVEL
Semiconductors and semimetals-Vol.ll, Solar Cells, pp. 50, Academic Press, 1975
[Ill-7]: Martin A. GREEN, Solar Cells, Ed. PRENTICE-HALL, U.S.A. page 96, (1982)
79
CHAPITRE IV
ETUDE D'UNE PHOTOPTLE BIJ!'ACIAI-,E ECLAIREE: PAR LES DEUX FACES
lNTRODUCTION
Dans cette partie, nous faisons L1ne étude en modélisation de la photopile bifaciale sous
double éclairement [IV -1.. 5]. Nous étudierons le photocourant et la phototension en différents
points de fonctionnement de la photopile L'influence du champ électrique cristallin et des
recombinaisons liées aux états d'interface sur ces paramètres sera mise en évidence.
Nous étudierons également la variation de la puissance électrique de la photopile selon Té point
de fonctionnement. "L'effet de phénomènes de recombinaison
Au cours de cette étude, nous ne prendrons en compte que la contribution de la base de la
photopile éclairée par les deux faces. Les études antérieures ont montré une faible contribution
de l'émetteur sur le photocourant. En effet, en négligeant la contribution de l'émetteur, nous
faisons une erreur relative inférieure à 1% dans le calcul en modélisation du photocourant
NOLIS dégagerons enfin l'intérêt que présente les photopiles bifaciales à partir de l'étude du
courant, de la tension et de la puissance électrique.
Sur la figure (IV-1), nous présentons le schéma simplifié d'une photopile bifaciale éclairée par
les deux faces.
L
.J
) L
tJ
tJ
<
;:J
<
) L
Base
) L
r-
"
t
] onction x = 0
Figure (IV-l): Schéma simplifié d'une photopile bifaciale éclairée par les deux faces
Dans ces photopiles, des contacts métalliques sont placés sur les faces avant et arrière de la
base afin de recueillir le photocoLirant
Nous nous intéresserons dans cette étude en
modéli~tio!1
en x = O.
1 ETUDE DE LA DENSITE DES PORTEURS
au passage des porteurs à la iC'r.C!~'.:'r.
80
En considérant que les deux éclairements sont indépendants l'un de l'autre, nous ferons
l'hypothèse que les densités de porteurs générés par les deux éclairements sont des grandeurs
additives. Ainsi, la densité des porteurs photogénérés est la somme algébrique de chacune des
densités de porteurs générés par chaque éclairement
En désignant cette résultante par Rp(x), il vient que
Rp(x) = np(x) + mp(x)
(IV-l)
Nous rappelons que dans cette équation: np(x) désigne la densité des électrons générés sous
J'action de l'éclairement par la face avant de l'émetteur, mp(x) la densité des électrons générés
sous J'action de l'éclairement par la face arrière de la base (Chapitres r et Ill).
Rp(x) désigne la densité des élec·trons générés sous l'action simultanée des deux éclairements.
Sur la figure (IV-2), nous représentons les profils de densité des porteurs Rp(x) en
fonction de la profondeur x de la base pour des photopiles de ditférentes qualités caractérisées
par leur champ cristallin E (en V/cm) et fonctionnant en circuit ouvert.
3.10 14 . - - - - - - - - - . - 1 - - - - - - ,
E ~ 15
.~.
-
~
-
o
1
o
0015
0.03
x(crn)
Figure (IV-2): Densité des porteurs en circuit ouvert ( SF n = Ocm/s) pour différentes
photopiles caractérisées par leur champ E ( en VIcm ) avec SB = 102crn/s
La figure (IV-2) montre que pour de faibles ,:a!e'-J;"s de la vitesse de reccmbinaison SF n
des porteurs à la jonction, le gradient des porteurs est inférieur ou égal à zéro. Les porteurs ne
peuvent donc pas traverser la jonction. C'est le phénomène qui se déroule en circuit ouvert. Ils
ne participent pas à la production du photocourant
Cette figure montre également que la densité des porteurs générés dans la base de la photopile
fonctionnant en circuit ouvert est plus importante dans une photopile où le champ cristallin est
plus élevé que dans une autre.
81
Enfin, nous observons que la génération des porteurs est importante il la jonction et sur la face
arrière pour une photopile subissant le double éclairement.
Sur la figure (lV-3), nous représentons les profils de densité de porteurs photogénérés dans la
base de différentes photopiles bifaciales caractérisées par leur champ cristallin E (en V/cm) en
fonction de la profondeur x de la base pour un point de fonctionnement intermédiaire.
2°10
13
---r')
1
E
u
18°10
13
....
CIl
::l
(1)
t
0
0.
16°10
/
r.
"--"
13
.
.
,
\
\-
-E=5
,
1
\
"
1> 15
CIl
(1)
-0
-(1)
13
c: 14°10
0
CIl
(1)
° 13
1.210
o
0.015
0.03
x(cm)
Figure (IV-3) Densité des porteurs pour SF n = 104 cm/s pour des photopiles caractérisées par
leur champ cristallin E ( en V/cm) avec SB = 104 cm/s
La figure (IV-3) montre que la densité des porteurs générés dans la base des photopiles
bifaciales pour le point de fonctionnement choisi présente plusieurs zones:
Une première zone proche de la jonction où le gradient de la densité des porteurs est positif.
Les porteurs situés dans cette zone peuvent traverser la jonction et participer à la production
dl! photocourant.
Une deuxième où le gradient de la densité des porteurs s'annule deux fois en passant par des
valeurs négatives. Les porteurs générés dans cette zone sont "bloqués" dans cette ïégion où ils
peuvent se recombiner.
Une troisième zone où le gradient de la densité des porteurs s'annule deux fois en passant par
des valeurs positives. Les porteurs situés dans cette zone peuvent se. déplacer seulement dans
cette région car en bordure de zone, leur gradient S'annule iis se recombinerons dans cette
zone. Ceux-ci ne participent pas à la production du courant.
Une quatrième zone enfin située près de la face arrière où le gradient des porteurs est inférieur
ou égal à zéro Ces porteurs ne participent pas à la production du photocourant.
Pour les porteurs qui ne participent pas à la production du courant et qui se trouvent dans les
deuxième, troisième et quatrième zone, la pho~opil~ semble être en circuit ouvert. La base
parait donc être réduite d'une quantité égale à l'épaisseur de là première zone. C'est le
82
phénomène de l'élargissement de la zone de charge d'espace observé dans les chapitres l, II et
Ill. Ce phénomène est également observé d'une photopile à J'autre lorsque le champ cristallin
diminue.
Sur la figure (IV-4), nous représentons les profils de densité des porteurs en fonction de la
profondeur x de la base de différentes photopiles bifaciales éclairées par les deux faces et
caractérisées par leur champ cristallin E (en VIcm) fonctionnant en court circuit.
)"10 14
. - - - - - - - - " ' T1- - - - - - - - - ,
,.......
r'"l
E
u
'-'
~
-
2"10 14 ,--
~
li)
t
o
!
0..
CIl
li)
~
i
1"10
14
"!
E=5
-
1
CIl
C
J
J
li)
o
1
,
.:.,...-~_
o
o
..
1
0.015
0.03
x(cm)
10 6cm/s pour des photopiles caractérisées par
Figure (IV-4): Densité des porteurs pour SF n =
leur champ cristallin E ( en V/cm) avec SB = Ocm/s
La figure (IV-4) montre que lorsque la vitesse de recombinaison SF n des porteurs à la
jonction est élevée, le gradient de la densité des porteurs à la jonction est positif Pour de telles
vitesses de recombinaison, les porteurs pourront donc traverser la jonction. Il n'y a donc pas de
stockage de charges. Ce mode de fonctionnement correspond au court circuit. Pour les
porteurs situés loin de la jonction et pour lesquels le gradient est positif, ils peuvent se
recombiner dans la photopile et ne pas participer à la production du courant.
Il ETUDE DU PHOTOCOURANT
Dans ce paragraphe, nous étudions le photocourant produit par la photopile éclairée sur
les deux faces. L'influence des recombinaisons aux interfaces sur le photocourant sera mise en
évidence. Une étude comparative des courants de court circuit délivrés par les photopiles sous
divers éclairements (éclairement côté émetteur, côté base et éclairement sur les deux faces)
sera effectuée.
83
A l'aide de la densité des pqrteurs Rp(x) produite par le double éclairement, nous déduisons la
densité de courant par:
(IV-2)
Sur la figure (IV-5) , nous représentons la densité de photocourant pour des photopiles
caractérisées par leur champ cristallin et éclairées sur les deux faces en fonction de la vitesse de
recombinaison SF n.
.---. 0.062
. NE
,E= 15
/
u
/
~
--...-
/
/
Vl
/
1
1
t::
...
0
üCl)
1
/
~
Vl
Cl)
. E.,:".5
1
1
/
0.031
"0
/
/
/
/
/
2
4
6
8
log(SFn)
Figure (lV-5): Densité de photocourant en fonction de SF n pour des photopiles caractérisées
par leur champ cristallin E ( en V/cm) avec SB = 104cm/s
La figure (IV-5) montre que les courbes de photocourant obtenues ont la même allure
que celles qui ont été précédemment représentées dans le cas d'un éclairement par la face avant
ou par la face arrière uniquement. Cependant, l'amplitude du photocourant produit par la
photopile sous double illumination (face avant et face arrière)est plus importante que dans les
autres cas.
La figure (IV-6) représente le profil de densité de photocourant des porteurs pour deux
photopiles 'de différentes qualités dont les bases sont quasi-neutres (E = avIcm).
84
OD3J
,/
'/
.--...
SFOn= l..e4-' ' j
-----
N
8w
1
1
~~
1
/
S
~
1
!
0.016
o
w
.....o
o
..c:
P-t
/
1
;SFOn=O
1
1
tJ'll "10
-5
-/"(
---'-
L--~
o
6.75
-'
13.5
log(SFn) .Figure (1 V-6): Densité de photocourant pour deux photopiles de différentes qualités en
fonction de SF n.
La figure (IV-6) du photocourant en fonction de la vitesse de recombinaison SF n des
porteurs à la jonction garde la même allure que celles qui ont été présentées précédemment
dans les cas d'un éclairement sur une seule face de la photopile. lei, elle dégage, pour un SfO n
donné, un effet plus important des effets des états d'interface aux environs du point de
fonctionnement du circuit ouvert en produisant un courant de fuite plus élevé dans le cas du
double éclairement de la photopile comparée au simple éclairement (face avant ou anière).
Pour une photopile de mauvaise qualité ( les recombinaisons aux interfaces sont importantes ),
une fraction importante du photocourant est absorbée dans les processus de recombinaisons
interfaciales pour tout point de fonctionnement, tandis que dans les photopiles de bonne
qualité, les recombinaisons interfaciales sont minimisées, ce qui provoque de faibles pertes dans
la photopile.
Dans le tableau (I V-1), nous présentons les valeurs calculées des courants de court
circuit pour les divers cas d'éclairement. Jcc 1 représente le courant de court circuit produit par
la photopile éclairée en face avant (côté émetteur), Jcc 2 celui produit par la photopile éclairée
en face arrière (côté base) et Jc c3 celui produit par la photopile éclairée sur les deux faces.
Nous présentons les courants de court circuit en supposant l'effet des états d'interface constant
quel que soit le côté de l'éclairement mais en gardant les recombinaisons en volume variables.
Nous avons calculé les courants de
leur champ cristallin E (en V/cm).
COLIrt
circuit pour différentes photopiles caractérisées par
85
Tableau (IV-1 ): Tableau de comparaison des courants de court circuit pour différentes
photopiles ( On = 26cm 2/s et H = 300l1m ).
Photopiles
Jcc 1
Jcc 2
E en V/cm
(mAJcm 2 )
(mAJcm 2 )
Ln = 100 I1m
Ln = 45 ).lm
0.35
A: E = 0
29
B: E= 5
32
C: E= 15
34
Jcc 3/Jcc l
Jcc3/Jcc2
3]
1.069
88.57
41
1.281
41
62
1824
10.33
Jcc 3
(mAJcm 2)
Ln = 100 /lm
6
Le tableau (IV -1) montre l'importance du double éclairement sur le courant de court
circuit pour une photopile. Le double éclairement permet d'obtenir environ 1.5 fois plus de
courant que l'éclairement par l'émetteur uniquement et près de 10 à 100 fois plus de courant
que l'éclairement par la face arrière de la base de la photopile.
III ETUDE DE LA TENSION
La tension Vr délivrée par la photopile est exprimée par l'équation de Boltzmann:
° [R (0)
V =~ln
r
Il
tA"n
p
R
0
l
+1
(IV-3)
p
Vr dépend du point de fonctionnement de la photopile. C'est une fonction de la vitesse
de recombinaison SF n des électrons à la jonction Sur la figure (IV-7), nous présentons la
variation de la tension pour des photopiles bifaciales de différentes qualités
86
0.631 r---"""~::::------',I--------'
-------_ ~On=le2
SfOn=l e4 ' , ',,-
,
" ,
,
"
ç:
o
.~
-
0.3161-
.....
o
Qj
......
o
..c:
Ç4
o
1
o
6.15
13 ..5
log(SFn)
Figure (IV-7): Tension délivrée par des photopiles bifaciales de différentes qualités en fonction
de SF n pour SB = 104 cm/s.
La figure (I V-7) de la tension en fonction de la vitesse de recombinaison SFn des
porteurs de charge à la jonction d'une photopile bifaciale soumise à des éclairements par ses
deux faces présente la même allure que celle qui ont été présentées précédemment dans les cas
où la photopile est éclairée par une seule face.
La tension de circuit ouvert est atteinte aux faibles valeurs de SF n. Elle diminue lorsque les
phénomènes de recombinaison aux interfaces deviennent importants.
Dans le tableau (IV-2), nous calculons la tension de circuit ouvert obtenue en modélisation
pour deux photopiles dont la qualité est caractérisée par les phénomènes de recombinaison aux
interfaces.
Tableau (IV-2): Calcul de la tension de circuit ouvert pour deux photopiles bifaciales de
différentes qualités.
SFO n (cm/s)
Photopiles
V co (mV)
A
632
B
590
Le tableau (IV-2) montre que la photopile A est de qualité supérieure à la photopile BLes
.
.
recombinaisons aux interfaces dans la photopile A étant moins importantes que les
recombinaisons aux interfaces dans la photopile B, la tension de circuit ouvert délivrée par la
photopile A est plus importante que celle qui est délivrée par la photopile B.
87
IV CARACTERISTIQUES COURANT-TENSION DE LA PHOTOPILE ECLAIREE
PAR LES DEUX FACES.
Nous présentons sur la figure (lV-8) les caractèristiques I-V obtenues en modélisation
pour des photopiles éclairées par les deux faces Elles sont obtenues en reliant à la tension, le
courant produit par la photopile en chaque point de fonctionnement.
""'
N
E
u
0062
1
=<
'-'
f/)
t:
E5
o....
\
u
1
~
~
~
<Il
~
\
"'Cl
i
§....
!
::l
o
U
o
o
...c:
p.
o
1
o
0.349
0.698
PhototcnsiOll CV)
Figure (IV-8): Caractéristiques courant-tension pour des photopiles bifaciales caractérisées par
leur champ cristallin pour SB
=
I04 cm/s.
Ces différentes caractéristiques montrent des similitudes avec celles qui ont été
présentées précédemment. Pour les faibles valeurs de tension ( fonctionnement de la photopile
au voisinage du court circuit ), le photocourant est maximal tandis qu'il est minimal au
voisinage aux grandes valeurs de tension ( fonctionnement de la photopile au voisinage du
circuit ouvert )
V ETUDE DU COURANT DE DIODE
En reécrivant l'équation (IV-2) avec les conditions aux limites (1-6) et (1-8) du chapitre
1 ( dans lesquelles la densité de porteurs est remplacée par Rp(x) ), et en tenant compte des
recombinaisons aux interfaces, la densité de photocourant s'exprime par:
(lV-4)
Posons:
(IV-5)
88
et
J"t(SFn)=qoSF1oRp(O)
(IV-6)
où J"t(SF n) est la fraction de courant qui traverserait la résistance de charge externe et
J"f(SF n) est celle qui est perdue à cause des états d'interface:
L'expression (IV-5) peut être reécrite sous la forme:
(IV-7)
En circuit ouvert, nous faisons les hypothèses suiv.<!ntes:
2°) SF 1 « (SFO n + IlnE)
La premiere hypothese conduit à: J" f (SFn)
~ q . (SFO n + ~ n . E)· R~ [ ex p ( ~~ )]
La seconde hypothèse permet d'écrire: J"f(SF n) »
j"t(SF n), ce
J r (SFn ) : : : J f (SFn) Ainsi, le photocourant se réduit au courant de fuite.
qui
conduit
à
Ce courant de fuite, qui est relatif à la vitesse de recombinaison aux interfaces, peut
être décomposé de la manière suivante:
J" f (SFn )=J" d (SFn )+J" r (SF)
n
(IV -8)
où
r
J " d(SFn)=q-SFOnoR Gp [ exp ( VT.-I
V )
]
(IV-9)
et
(IV-10)
J"d(SF n) est la fraction du courant de fuite de la photopile sous éclairement qui est
proportionnelle à un courant de diode sous obscurité et J" r(SF~) ( courant de saturation) est
celle qui traverserait une résistance placée en parallèle avec la diode.
En court circuit, nous pouvons faire l'hypothèse suivante: SF 1 » (SFO n + IlnE), ce qui
conduit à: J r (SFn ) : : : J" t (SFn ). Dans ce mode de fonctionnement alors, le photocourant est
presque entièrement délivré dans le circuit extérieur.
89
Dans un mode de fonctionnement intennédiaire, les recombinaisons liées aux effets
d'interface et celles liées à la résistance de charge externe sont à prendre en compte
La figure (IV-9) représente la variation du courant de diode en fonction de la
phototension pour SFO n = l02cm/s
0.03
1
1
\
"......
N
E
u
~
'-'
-
'Q)
002
e-
-
ï::::
::l
u
Ul
.0
0
=0
§....
E •
'-
I~
i
0.01
-
[ . S'
1
::l
0
E
1
1
0.2
0,4
0.6
0
0
oi
AJ
U
1
OR
Phototension (V)
Figure (IV-9): Courant de diode pour des photopiles bifaciales caractérisées par leur champ
cristallin pour SFO n = l02cm/s et SB
=
l04cm/s en fonction de la tension Vr
La figure (IV-9) montre que lorsque la photopile fonctionne en circuit ouvert ( faibles
valeurs de la vitesse de recombinaison des porteurs à la jonction ), la tension délivrée par la
photopile est importante et à ce point de fonctionnement, le courant de diode est élevé
En court circuit ( grandes valeurs de la vitesse de recombinaison des porteurs à la jonction ), le
courant de court circuit est important et la fraction de courant qui traverse la diode est faible.
La tension de circuit ouvert et le courant de court circuit sont d'autant plus importants que la
photopile est de bonne qualité.
VI ETUDE DE LA PUISSANCE DELIVREE PAR LA PHOTOPILE
Nous faisons une étude en modélisation de la puissance électrique de' la photopile
éclairée sur les deux faces. Une étude comparative de la puissance maximale délivrée par les
photopiles sous divers éclairements ( éclairement côté base, côté émetteur et éclairement sur
les deux faces) sera effectuée.
90
En partant de l'hypothèse que les seules pertes qui ont lieu dans la photopile sont causées par
les états d'interface ( caractérisées par la vitesse de recombinaison SfO n ), la puissance
électrique de la photopile s'exprime par:
Pr
-_c
l".·V
r
(IV-11)
r
La figure (l V-10) représente la variation de la puissance de trois photopiles bifaciales
caractérisées par leur champ cristallin en fonction de la vitesse de recombinaison SF n à la
jonction des électrons.
0.036
1
--------------:-------E~-
15
E ... :j
\
r>J?
"-
..
"
".
\
,
1
!
1
/
o
o
6.7"
13.5
log(5l'n)
Figure (IV- 10): Puissance électrique délivrée par des photopiles éclairées par les deux faces en
fonction de la vitesse de recombinaison des électrons à la jonction pour SB == 104 cm/s
La figure (IV- 10) montre que la puissance de la photopile est faible au voisinage du
court circuit ( grandes valeurs de la vitesse de recombinaison des porteurs à la jonction) et au
voisinage du circuit ouvert ( faibles valeurs de la vitesse de recombinaison des porteurs à la
jonction ). La puissance maximale est délivrée en un point de fonctionnement intermédiaire de
la photopile.
Lorsque le champ cristallin ( accélérateur des porteurs) augmente d'une photopile à l'autre, la
puissance maximale de la photopile augmente.
Dans le tableau (IV-3), nous comparons les puissances maximales PmI, P m2 et Pm3
obtenues en modélisation. PmI est la puissance maximale délivrée par une photopile éclairée
par ['émetteur, Pm2 est celle qui est délivrée par une photopile éclairée par la base et Pm3 est
celle qui est délivrée par une photopile éclairée par les deux faces.
91
Ces vaJeurs de puissances maximales sont produites pour différentes photopiles caractérisées
par leur champ cristallin.
Tableau (lV-3): Tableau de comparaison des puissances maximales calculées pour diftërentes
photopiles bifaciales (H = 30011m et SB
Photopiles
PmI
(mW/cm 2 )
P m2
PmJ
(mW/cm 2 )
(mW/cm 2 )
Ln = 100gm
Ln = 4SIJ.m
A: E = 0
15
B: E= 5"
C:E=IS
E(V/cm)
.
=
104cm/s)
PmJ/P m l
PmJ/P m2
0.136
Ln = 1001lm
16
1.067
117.6
17
0.431"
22
1.294
51.04
19
3.00
36
1.895
12
Le tableau (IV-3) montre que la puissance maximale délivrée par une photopile éclairée
suivant les deux faces est d'environ 1.5 fois plus élevée que celle qui est délivrée par la même
photopile éclairée suivant l'émetteur et d'environ 10 2 à 10 3 fois plus élevée que lorsque la
photopile est éclairée par la face arrière de la base.
VIl ETUDE DE LA RESISTANCE DE CHARGE
La charge externe est le paramètre qui fixe le point de fonctionnement de la photopile.
La fraction de photocourant qui traverse cette charge externe sous une tension Vr est Jn t
L'expression de la résistance de charge est:
R
r
Vr
=J"
t
(IV-12)
Nous représentons sur la figure (IV-1 1) la vitesse de recombinaison SF n des porteurs
de charge à la jonction en fonction de la charge externe d'une photopile éclairée par les deux
faces.
92
4
o
.--l.
35.n7
289.074
---'
)4292
Résistance de charge (O. cmD
Figu;e (IV-Il) Variation de SFn en fon~ti~n de la résistance de charge pour SFO n = i 02cOl/ s.
La figure (IV-11) montre que pour une charge externe élevée, la vitesse de
recombinaison des porteurs à la jonction est faible. Les grandes charges externes imposent
donc à la photopile un point de fonctionnement proche du circuit ouvert.
Quant aux faibles valeurs de charges externes, elles imposent à la photopile un point de
fonctionnement voisin du court circuit.
IIX
ETUDE DE LA CAPACITE DE L'ELARGISSEMENT DE LA ZONE DE
CHARGE D'ESPACE
L'étude de la densité des porteurs a montré un phénomène d'élargissement de la
jonction lorsque la vitesse de recombinaison SF n des porteurs à la jonction augmente. Ce
même phénomène est observé dans deux photopiles lorsque le champ cristallin diminue d'une
photopile à l'autre. Nous associons à l'élargissement de la jonction une capacité Cr qui dépend
de la densité des porteurs, dont l'expression est:
q.Rp(O)
C =---r
V
r
(IV-13)
La figure (IV-12) montre la variation de la capacité Cr correspondant à l'élargissement
de la jonction en fonction de la vitesse de recombinaison SF n des porteurs
93
, - - - - - - -1r - - - - - - - ,
:2 • 10 - 5
..•.
-~''',-
\
\
Î
\
-
\
\ \.
"\
o
1
o
3
~----- ..
6
log(Sfn)
Figure (IV-12): Capacité de l'élargissement de la zone de charge d'espace en fonction de SF n
pour. SB =.103 cmls
La figure (lV-12) montre qu'au voisinage du circuit ouvert ( SF n -. 0 ), la capacité de
l'élargissement de la jonction est importante tandis qu'elle est tàible lorsque la photopile
fonctionne au voisinage du court circuit.
En circuit ouvert, il y a stockage de charge à la jonction de la photopile, ce qui n'est pas le cas
en court circuit où les charges générées près de la jonction la traversent pour être collectées
sur les grilles.
Du point de vue quantitatif, l'influence du double éclairement sur la capacité de l'élargissement
de la photopile n'est pas remarquable. Lorsque la photopile est éclairée par l'émetteur ou par
les deux faces, la capacité de l'élargissement de la zone de charge d'espace, qui n'est
significative qu'en circuit ouvert, garde le même ordre de grandeur (
~
20l-lF ). Cela peut être
dû au fait que l'éclairement par la face arrière génère peu de porteurs à la jonction entre
l'émetteur et la base de la photopile, comparée à l'éclairement par la face externe de l'émetteur.
CONCLUSION
Au cours de celte étude en modélisation de la photopile bitàciale fonctionnant en
régime statique, nous avons mis en évidence l'importance de ce type de photopile par rapport
'aux photopiles conventionnelles.
Le CDurant et la puissance produits dans une photopile bifaciab 50nt plus importants que ceux
que délivre une photopile conventionnelle.
Les recombinaisons introduites par les états d'interface causent une diminution sensible de la
tension de circuit ouvert et augmentent les pertes de courant dans la photopile.
L'étude de l'émetteur de la photopile nous a permis de montrer que celui-ci participe peu à la
produ~tion
du photocourant global.
94
A partir de notre étude, la photopile sous illumination constante est équivalente à un
condensateur plan à charge constante et pour lequel l'écartement e des armatures est variable
(Figure (l V-13»
o
v
o
Figure (IV-13): Equivalent électrique d'une photopile sous illumination constante
Lorsque l'écartement e des armatures du condensateur est petit, la tension V est élevée, ce qui
correspond pour la photopile au fonctionnement en circuit ouvert. La capacité C du
condensateur est alors élevée.
Lorsque l'écartement e des armatures du condensateur est grand, la tension V est faible: C'est
le cas où la photopile fonctionne en court circuit. La capacité C du condensateur est alors
faible.
95
B:ffiLIOGRAPHI:E
[IV-]]: A. CUEVAS, A. LUQUE, l EGUREN, J. DEL ALAMO
"High Efficiency Bifacial Back Surface Field Solar CeUs"
SJll~LCe))s,
Vol. 3, n04, pp. 337-340
1981
[IV-2]: J. EGUREN, J. DEL ALAMO, A. LUQUE
"Optimisation of p+ Doping Level of n+ p p+ bifacial B SF. Solar Cells By Ion Implantation"
Electron. Letters Vol. 16, n016, pp.633-634, 1980
[IV-3]: A. LUQUE, J.M. RUIZ, A. CUEVAS, J EGUREN, 1. SANGRADOR, lM. AGOST'
GOMEZ, G. SALA, l bEL ALAMo.
"Static Coneentrated Array With Double Side Illuminated Solar Cell" Energia Solare e Nuove
Prospettive. Comples., Conferenza Intrenazionale., Milano, IT AllA, Vol. l, pp 421-429 1980
[IV-4]:
M.
YA
BAKIROV,
R.
S.
MADATOV,
M.
YU
MUSTAFAEVA.
M.
ALLAKHVERDIEV, R. B. GASYMOV
"Bifacial Solar Cell" Geliotehnika (Taskent) Caden GLOTTAY, pp 64-65 1987
[IV-5]: Daniel L. MEIER, leong-Mo HWANG and Robert B. CAMPBELL
"The Effect of Doping Density and Injection Level on Minority-Carrier Lifetime as Applied to
Bifacial Dendritic Web Silicon Solar CeUs" I.E.E.E. Transactions on Electron Deviees, Vol.
E.D.-35, nO l, pp. 70-79 lanuary 1988.
96
CHAPITRE V
METHODES DE DETERMINATION EN REGIME STATIQUE DES PARAMETRES
ELECTRONIQUES ET ELECTRIQUES D'UNE PHOTOPILE
INTRODUCTION
Différentes techniques de détermination des paramètres caractéristiques des photopiles
ont été développées afin d'influer sur les techniques de fabrication pour améliorer leurs
performances parmi lesquelles des téchniques en régime statiques [V -\ .. 3]
Ce chapitre est consacré à la détennination des paramètres électroniques et électriques
d'une photopile fonctionnant en régime statique sous éclairement multispectraL Nous
proposons une technique de détermination des vitesses de recombinaison SFO et SB ( à la
jonction et à la face arrière de la base ) et de la longueur de diffusion L des porteurs
minoritaires.
Nous proposons également une technique de détennination de paramètres électriques tels que
la résistance shunt et la capacité correspondant à l'élargissement de la zone de charge d'espace.
1 TECHNIQUE DE DETERMINATION DES PARAMETRES ELECTRONIQUES
}O)
Détermination de la longueur de diffusion L et de la vitesse de recombinaison SB des
porteurs dans la base de la photopile.
La solution SB2 (équation (1-13» de l'équation (l-l\) représentant le photocourant en
fonction de la vitesse de recombinaison SB des p011eurs sur la face arrière ( Chapitre J,
paragraphe (III) ) est une fonction de la longueur de diftùsion L des électrons L'équation (lIl) est valable en court circuit ( SF > 10 7crn/s ). En remplaçant alors SB2(L) dans l'équation
(l-9) représentant la densité J n de photocourant, l'expression de J n obtenue est celle du courant
de court circuit en fonction de la longueur de diffusion L.
La fonction Jsc(L) étant obtenue, pour une valeur mesurée Jsc de courant de court circuit,
correspondra une valeur de L qui est obtenue par l'intersection entre les courbes Jsc(L) et J sc .
Jsc(L) est une fonction de calibration [V-4].
La figure (V-l) représente Ja fonction de calibration Jsc(L) et une valeur du courant de
court circuit Jsc = 30.2mA pour une photopile dont la base est d'épaisseur
300~tm.
97
0032
__ J.sc
....
./
.
;.;:.::~.
__~-::-::
~~
...-.
./
.".
./
.../"r
CI>
ç:
o
b
l
u
!
lU
CIl
/
i
:a:i
lU
./
0.019
/
-0
f
~
1
~
l
o
u
i
o
.....
o
..c:
p..,
0.007
o 01
o
0.02
L(cm)
Figure (V-1): Détermination de la longueur de diffusion L des électrons par la technique de
l'intersection des courbes théorique et expérimentale de courant de court circuit.
Le tableau (V-1) représente les valeurs de longueur de diffusion L de durée de vie
T
et
de vitesse de recombinaison des électrons sur la face arrière de la base déterminées par notre
méthode. Les valeurs expérimentales de courant de court circuit [V-5] ont été mesurées pour
différentes photopiles.
Tableau CV -1 ): Détermination de L
et SB pour différentes photopiles
( H = 3001lm, D = 26cm 2 /s )
Photopiles
Jsc (mNcm 2 )
SFsc(crn/s)
T
LÜlm)
1: (
ilS )
à 13%
POLYX GBS
30.2
10 8
SB(crn/s)
à9%
ISO
8.65
5.51710 3
170
Il. 12
5.013 10 3
210
16.26
4.353 10 3
27-2A
POLYX GBS
30.5
28-lA
POLYX GBS
31
"
24-lC
2°) Discussions
Différents facteurs limi tatifs du courant de court circuit peuvent influencer la
détermination des paramètres du tableau (V-1) par notre technique. Parmi ces facteurs, nous
avons la préc~sion de mesure du courant de court circuit, celle de l'ép~isseur de la base de la
photopile et du coefficient de diffusion des porteurs de charge.
98
Nous effectuons une étude de J'influence de chacun des paramètres ci-dessus cités sur notre
technique de détermination des
paramètïe~
Erreur relative (l1J/J) du courant de court
de la photopile
cirç\JjL~ur
l<u:jétermination de L
Nous avons développé la technique de détermination de la longueur de diffusion L des
porteurs en considérant que la contribution de l'émetteur sur le courant de court circuit de la
photopile est négligeable ( cette contribution est de l'ordre de
J %:
Chapitre IV). Cette
hypothèse nous permet de trouver des valeurs de longueur de diffusion acceptables ( à 13%
près ).
Dans le tableau (V-1), Jes valeurs expérimentales de courant de court circuit sont conrïues à
10% près.
L'erreur de mesure peut donc être négligée paï rapport à l'erreur de modélisation.
Erreur relative (l1HJH) sur le courant de
COUlt
circuit
Nous présentons dans le tableau (V-2), les valeurs de courant de court circuit obtenues
en modélisation pour différentes valeurs de l'épaisseur H de la base
Tableau (V-2): Erreur de modélisation sur Jsc de H ( 0
H (!lm)
270
30
=
26cm 2/s )
290
30
--------------'--------
Ce tableau montre qu'une erreur de 7% sur la mesure de H n'introduit pas d'erreur à 1%
près sur la détermination du courant de court circuit en modélisation.
De même une erreur relative de Il % sur la mesure de H n'introduit pas d'erreur à 1% près sur
le courant de court circuit obtenu en modélisation pour une photopile dont le coefficient de
diffusion des porteurs minoritaires 0 est 26cm 2/s
Erreur relative (l1D/D) sur le courant de CQurt circuit
Nous présentons dans le tableau (V-3), les valeurs de courant de court-circuit obtenues
en modélisation pour différentes valeurs du coefficient de diffusion 0 des porteurs.
· 99
Tableau (V-3): Erreur de modélisation sur J sc de 0 ( H
Jsc (mA)
= 300~m
24
28
JI
31
)
Ce tableau montre qu'une erreur de 11 % sur la mesure de D n'introduit pas d'erreur à 1% près
sur le courant de court circuit en modélisation.
Des méthodes de mesure [V -6.9] du coeftlcient de diffusion 0 des porteurs
minoritaires et de l'épaisseur H de la base de la photopile sont considérées comme bonnes si la
précision de mesure de ces paramètres est de l'ordre de "10%.
Ainsi, la fonction de calibration JsC<L) que nous avons calculée n'introduit pas d'erreur
sensible sur la détermination de L, si l'émetteur de la photopile introduit une erreur de mesure
inférieure ou égale à 1% du courant de court circuit. Ce cas se produit pour les photopiles dont
l'émetteur présente les caractéristiques définies au Chapitre Il (paragraphe (1)) Dans ce cas
alors, la technique est applicable
Enfin, les résultats de longueur de diffusion obtenus dans le tableau (V-1) sont en
accord avec ceux qui sont produit par des mesures de réponse spectrale [V-5].
Il TECHNIQUE DE DETERMINATION DES PARAMETRES ELECTRIQUES
Dans cette partie, nous déterminons les paramètres électriques de la photopile en nous
servant de la longueur de diffusion L et de la vitesse de recombinaison SB des porteurs de
charge calculées précédemment
La tension de circuit ouvert
des photopiles étudiées
précédemment est
mesurée
expérimentalement par les auteurs.
1°) Détermination de la vitesse de recombinaison SFO n introduites par les états
d'interface
Lorsque la photopile fonctionne au vOlsmage du circuit ouvert, la vitesse de
recombinaison des porteurs de charge à la jonction se réduit à la vitesse SFOn introduite par les
états d'intertace.
La tension V délivrée par la photopile est la tension de circuit ouvert Vco. Elle est une fonction
de la vitesse SFO n- Nous obtenons alors une nouvelle fonction de calibration Vco(SFO n).
,.
_0 •
....
"
..
100
.La mesure de la tension de circuit ouvert d'une photopile permet de déterminer la valeur de
n
SFO par la technique dël'intersection entre la fonction de calibration Vco(SFO n) etla tension
de circuit ouvert Vco mesurée expérimentalement.
La figure (V-2) indique la technique de détermination de la vitesse de recombinaison
SFO n pour une tension de circuit ouvert Vco = 592mV
0.0&5
o
7.5
15
log(SfOn)
Figure (V-2): Technique de déterInination de SFO n
Le tableau (V-4) représente les valeurs de la vitesse de recombinaison SFO n à la
jonction des porteurs caractérisantJes effets d'interface pour les photopiles du tableau (V-1 )
Tableau (V-4): Détermination de la vitesse de recombinaison SFO n
Photopiles
POLYXGBS
V cn
log(SFO n)
(mV)
(cm/s)
589
4.08
592
4.06
596
3.98
28-IA
POLYXGBS
27-2A
POLYXGBS
24-1C
Ce tableau de mesures de SFO n caractérise les effets des états d'interface. Lorsque les
effets d'interface sont importants, la tension de circuit ouvert est faible.
2°) Détermination (je la r~~istanceshunfRsho et-(Je la c'apacitê Co de l'élargissem~nt de .
. la zone de. charge d'espace
101
A partir du tableau (V-4), nous calculons la rësistance shunt et la capacité de
l'élargissement de la zone de charge d'espace de la photopile.
Tableau (V-S): Détermination de Rsho et de Co
Photopiles
10g(SFO n)
(cm/s)
Rsho
(O.cm2 )
Co
OlF.cm- 3 )
4.08
22.86
4.17
POLYXGBS
. ...
27-2A
4.06
23.09
;4.32
POLYXGBS
3.98
24.12
5.07
POLYXGBS
28-1A
'
'
..
24-1C
Le tableau (V-S) montre que lorsque les effets d'interface deviennent importants
(recombinaisons interfaciales importantes), la résistance shunt diminue de même que la
capacité de l'élargissement de la zone de charge d'espace diminue; La diminution de la
résistance shunt se traduit par une augmentation des pertes de courant dans les états
d'iriterface. La diminution de la capacité de l'élargissement de la zone de charge d'espace a été
interprétée comme une augmentation de la vitesse de recombinaison à la jonction des porteurs
ou une diminution du champ cristallin.
L'augmentation des phénomènes de recombinaison aux interfaces se traduit par une diminution
de la qualité de la photopile,
III
APPLICATION
DE
LA
TECHNIQUE
DE
DETERMINATION
DES
PARAMETRES A UNE PHOTOPILE ECLAIREE PAR LA FACE ARRIERE
Dans le chapitre III, nous avons déterminé la vitesse recombinaison SB des porteurs à
la face arrière de la base correspondant à la photopile éclairée par la face arrière.
Nous faisons l'hypothèse que la photopile que nous étudions possède un émetteur dont les
caractéristiques respectent les conditions d'application de la méthod~.
La figure (V-3) indique la technique de détermination de la longueur de diffusion L à
partir de l'intersection entre la densité de courant Jsc(L) obtenue en modélisation en f~nction
de la longueur de diffusion et du courant de court circuit mesuré expérimentalement.
102
8
0.009
..r/~-
1
8
-"f-'
//
.~.
,~J
".
1j
i<::l
~
,,1
0.005 -
U
/
~
~
......
ë
Jsç= 0.00296
_
1
-(1)
.-
.~
I--l
-
!
1
".-
f'~
1
0 '""--------'----------'
o
0.02
0.01
L(cm)
. . . _ :. Ei~re (V'-~): Tec~qlle de détermination deJa longueur de diffusion L pQ~r une photopile
éclairée par-laface arrière.
• ,
Dans le tableau (V-6), nous présentons les valeurs de longueur de diffusion L
déterminées par notre technique pour une photopile soumise à des éclairements d'intensité
variable:
Tableau
CV-6): Détermination de L et SB ( H =
Int. lum.
(mW/cm2 )
Jsc [V-lO]
(Ncm 2)
100
160Jlm et NB = 3.10 16cm-3 )
SF
L(Jlm)
à 13%
0.00296
(cm/s)
108
40
0.61
34.2
0.000957
"
30
0.34
1.9 104
2.6 104
10.9
0.000299
"
20
0.15
3.9 104
't(Jls)
SB(cm/s)
à9%
Le tableau (V-6) présente les longueurs de diffusion L, les vitesses de recombinaison SB, ainsi
que les durées de vie
't
des porteurs déterminées par notre technique pour une photopile
éclairée par sa face arrière. Les durées de vie sont faibles pour l'éclairement en face arrière de
la base pour la photopile que nous venons d'étudier. Ceci provient du fait que l'éclairement en
face arrière génère peu de porteurs à la jonction de la photopile d'où un courant de court
circuit faible.
CONCLUSION
Nous venons de proposer des techniques de détermination des paramètres électroniques
et électriques des photopiles.
103
La technique (le détermination des paramètres électroniques de la photopile repose sur la
mesùre du courant de court circuit. EUe pennet de calculer la longueur de diffusion L, la
vitesse de recombinaison SB à la face arrière et la durée de vie t des porteurs générés par la
lumière excitatrice avec une précision d'autant plus bonne que la mesure du courant de court
circuit est précise.
Cependant, la technique n'est applicable que pour les photopiles dont la contribution de
l'émetteur au photocourant est de l'ordre de 1%.
La technique de détennination des paramètres électriques quant à elle repose sur la mesure de
la tension de circuit ouvert. Elle pennet de détenniner la
résistanc~
shunt et capacité de
':l'élai-gissèment -de la zone ,de charge d'espa~è par-ole caicut la vitesse ~e re"ë"ombinaison SFO-
- -Ccaractérisant les états d'i~terface) des porteurs à la jonction.
104
BIBLIOGRAPHIE
[V-1]: G. C. JAIN, S. N. SINGH and R. KOTNALA
"Diffusion Length Determination in n+pp+ Structure Based in Silicon Solar Cells From the
Intensity Dependance of the Short Circuit CUITent for Illumination from the p+ Side" Solar
Cells 8 pp. 239-48, 1983
[V-2]: S. K. SHARMA, S. N. SINGH, B. C. CHAKRAVARTY and B. K. DAS
"Determination of Minority Carrier Diffusion Length in p-Silicon Wafer by PhotocuITent
Generation Method" 1. Appl. Phys.,.60 (10) pp. 3550-52, 1986
[V-3]: L. SAMAJ • ,
"Lifetime of Minority Carriers in Polycristalline Semiconductors" Phys. Stat. Sol. (a) 10 l, 137
pp. 137-141 (1987)
[V-4]: G. SISSOKO, E. NANEMA, Y. L. B. BOCANDE, A. L. NDIAYE, M. ADJ
"Minority Carrier Diffusion Length Measurement In Silicon Solar Cel1 Under Steady Constant
White Bias Light" Proc. 5th. World Renewable Energy Congress, pp. 1594-1597 15-21 June
Denver (V.S.A.) 1996
[V-5]: Le Qwang NAM, M. RODOT, M. GHANNAM, J. COPPYE, P. de SCHEPPER, 1.
NUS, D. SARTI, 1. PERICHAUD, S. MARTINUZZI
"Solar Cells with 15,6% Efficiency on Multicrystalline Silicon, using Impurity Gettering, Baek
Surface Field, and Emitter Passivation" Int. 1. Solar Energy Vol.1l, pp. 273-279, 1992
[V-6]: S. SIVOTHAMAN, L. Q. NAM, M. RODOT, 1. NIlS, M. GHANNAM, 1. COPPYE,
G. PALMER, D. SARTI
Proc. Il th European Photovoltaïe Solar Energy Conference and Exhibition, 1992
[V-7]: M. A. GREEN
"High Effieieney Silicon Solar Cells", Trans. Tech. Publication (1987)
[V-8]: M. KuNSTAN and A. SANDER
Semicond. Sei. Technol. 7, (1992), pp. 51-59
[V-9]: LANDOLT-BÙRNSTEIN
New Series 1982; VoI.17(a)
~d.
O. Madelerng (Berlin: Springer)
105 .
[V-10]: Daniel L. MEIER, Jeong-Mo HWANG and Robert B. CAMPBELL
"The Effect of Doping Density and Injection Level on Minority-Carrier Lifetime as Applied to
Bifacial Dendritic Web Silicon Solar Cells" I.E.E.E. Transactions on Electron Deviees, Vol.
E.D.-35, n°1, pp. 70-79 January 1988.
106
CONCLUSION ET PERSPECtIVES
L'étude que nous venons d'effectuer sur la photopile bifaciale en fonctionnement en
régime statique sous éclairement multispectral nous a permis de comparer quantitativement la
part contributive de la base et de l'émetteur au photocourant global.
Il en est ressorti que le photocourant global est presque entièrement produit par la base de la
photopile. La contribution de l'émetteur au photocourant est négligeable,
Cette étude nous a conduit à considérer une nouvelle composante SF opt de la vitesse
de recombinaison SF à la jonction des porteurs qui est due aux effets de l'excitation optique.
- Elle nous a àussi êërioùits' à
vitesse de
prendre\~n '~OIÎ1'pte une éompo-santé liée à l'éclairement po~r la
recomblnais~n'SB 'à la face arrière des porteu'rs.
.
Au cours de cette étude, nous avons également proposé des méthodes de détermination
des paramètres électriques et électroniques de la photopile.
La méthode de détermination des paramètres électroniques que nous proposons repose sur la
mesure du courant de court circuit de la photopile. Elle conduit à la détermination de la durée
de vie
't,
de la longueur de diffusion L et de la vitesse de recombinaison SB des porteurs
minoritaires de charge en excès sur la face arrière.
La méthode de détermination des paramètres électriques quant à elle repose sur la mesure de la
tension de circuit ouvert. Elle conduit à la détermination de la composante de la vitesse de
recombinaison à la jonction des porteurs qui caractérise les phénomènes de recorIJ,binaisons aux
interfaces de la photopile. La détermination de cette composante permet de calculer la
résistance shunt et la capacité de l'élargissement de la zone de charge d'espace de la photopile.
L'influence du champ électrique cristallin sur les paramètres de la photopile a également été
, examinée. Nous avons considéré la composante du
cham~
qui accélère les porteurs de charge
générés.
De nouveaux axes d'étude peuvent être développés à partir de l'étude en modélisation de la
photopile que nous venons d'effectuer. Quelques-uns de ces axes sont:
1°) Dans l'étude en modélisation dè la photopile, la capacité de l'élargissement de la
zone de charge d'espace est assimilée à celle d'un condensateur plan. Il devrait donc être
possible de déterminer la constante diélectrique du matériau ayant servi à fabriquer la,!
photopile.