TD 02 / ph 102 d / I1 – ESIEE 2006 ① Loi de Child – Langmuir dans

TD 02 / ph 102 d / I1 – ESIEE 2006
Page 1 sur 3
c Loi de Child – Langmuir dans une diode à vide
Deux plaques métalliques planes, de surface S et distantes de d, sont soumises dans le vide à une
d.d.p U. Une des plaques, la cathode, dont le potentiel V0, est pris comme référence, émet des
électrons par effet thermoélectronique. Ces électrons sont captés par l'autre plaque, l'anode,
polarisée positivement: Vanode = U > 0. Le courant volumique est supposé uniforme.
1) Établir, à l'aide du théorème de l'énergie cinétique et de l'équation de Poisson, l'équation
différentielle à laquelle satisfait le potentiel V en fonction de la distance x à la cathode.
2) Trouver la relation I(U) entre l'intensité I et la d.d.p U; on admettra que le champ électrique
est nul pour x = 0.
d Distance de Debye
I. Si la concentration n (n = nombre de porteurs de charge par unité de volume) n'est pas uniforme,
il apparaît un courant de diffusion dont l'expression est donnée par la loi de Fick : Jd= − D grad(n)
où D est le coefficient de diffusion.
1) Ecrire la condition d'équilibre électrique entre les courants de conduction et de diffusion
pour un métal que l'on assimilera à un gaz d'électrons libres, de densité n, de mobilité µ,
évoluant dans un réseau d'ions fixes de concentration n0. On admettra que |n – n0| << n0 ;
2) Déduire (théorème de Gauss) l'équation différentielle, satisfaite par le champ électrique :
2
D
λ
−=∆ E E où 2
e0
0
Den
D
⋅µ⋅
⋅ε
=λ est la longueur de Debye. N.B. : 9
0
1910 u.SI
4≈⋅ πε .
II. Comme la diffusion s'oppose à l'accumulation de charges électriques sur la surface d'un
conducteur en équilibre, les charges se repartissent sur une certaine épaisseur que l'on se propose
d'évaluer. Pour atteindre cet objectif il faut résoudre l'équation différentielle, établie ci-dessus (loi
de Fick), dans le cas où une surface plane limite le conducteur.
1) En déduire que les charges se répartissent sur une couche d'épaisseur égale à quelques
longueurs de Debye λD.
2) Evaluer λD dans le cas d'un conducteur métallique (Cu) dont le coefficient de diffusion
s'écrit : Fe E
3
2
D⋅µ⋅= . On prendra n0 = 1029 m−3 et EF = 7 eV ;
3) Calculer, pour le métal Cu, τ (la durée de relaxation de la vitesse de dérive ou vitesse de
drift) et la mobilité
e
m
eτ⋅
−=µ en sachant que
2
e
e
ne
m
⋅
τ⋅
σ= . A.N. : la conductivité du cuivre
σCu ≈ 0.5·106 Ω−1·m−1 ; la concentration des porteurs dans le cuivre : ne ≈ 0.9·1029 m−3 ; la
masse de l’électron me ≈ 0.9·10−30 u.SI (kg) et la charge de l’électron |e| ≈ 1.6·10−19 u.SI (C).
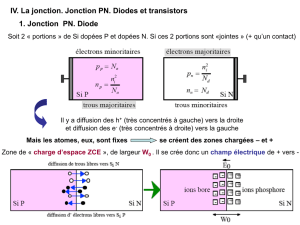
e Jonction p-n
On réalise une jonction p-n en dopant différemment deux parties d'un matériau semi-conducteur :
l'une de type p contient un excès de trous, l'autre de type n contient un excès d'électrons. La forte
inhomogénéité de la concentration des porteurs qui en résulte donne naissance à un double courant
de diffusion : les trous, majoritaires dans p, diffusent vers n et réciproquement les électrons,
majoritaires dans n, diffusent vers p. Par conséquent p se charge négativement et n positivement, ce
qui crée au niveau de la jonction, un champ électrique interne Ein0 orienté de n vers p (Fig. la). Par
son action sur les porteurs, ce champ limite la diffusion. Un équilibre s'établit alors entre courant de
diffusion et courant de conduction. En électronique, le composant constitué d'une jonction p-n
enfermé dans un boîtier protecteur est appelé une diode à jonction.

TD 02 / ph 102 d / I1 – ESIEE 2006
Page 2 sur 3
Fig. 1a
Considérons une diode p-n avec deux bornes, l'une P reliée à la région p et l'autre N reliée à la
région n. Si l'on applique une tension U = UAB = VA - VB, ce qui revient à appliquer un champ
électrique Ea le champ électrique interne qui agit sur les porteurs devient : Ei = Ein0 + Ea.
(1) Si la diode est polarisée en direct (U > 0), le champ électrique interne Ei est plus faible que Ein0.
Le déplacement des porteurs majoritaires est facilité et le courant passe entre A et B. Son intensité I
croit très rapidement avec la tension U jusqu'à atteindre quelques ampères pour une tension de
quelques volts.
(2) Si la diode est polarisée en inverse U < 0, Ei est plus intense que Ein0. Le courant n'est dû qu'à la
circulation de porteurs minoritaires. U intensité correspondante de ce courant inverse est très faible
Caractéristique de la diode à jonction
Fig. 1b
On constate que le comportement de la diode dépend de façon spectaculaire du signe de la tension
U (Fig. lb) :
Une allure fortement dissymétrique de la caractéristique rend la diode pratiquement équivalente à
un court-circuit dans le sens direct et à un circuit ouvert dans le sens inverse.
Ces propriétés de non-linéarité qui distinguent la diode des conducteurs ohmiques sont très utilisées
dans les circuits, notamment pour redresser des courants alternatifs. La caractéristique se trouve
dans le premier et le troisième quadrants : la diode est donc un récepteur (Fig. 1b).
La caractéristique I(U) de la diode à jonction a pour expression :
00
U
IIexp 1
U
=− où
23 4
B
019
kT1.4 10
UT0.910T
e1.6 10
−−
−
⋅×
=≈ ⋅≈×⋅
×
.
i) Calculer U0 à la température ambiante T 300 K.
ii) I0 = 5 µA ; calculer I(U) pour U = −5V, −2V, 0V, 0.1V, 0.5V et 5V. Conclure.

TD 02 / ph 102 d / I1 – ESIEE 2006
Page 3 sur 3
f Convertisseur photoélectrique – Effet photovoltaïque
En éclairant un semi-conducteur avec des photons dont l'énergie est supérieure au gap, on crée des
paires électrons-trous et par conséquent on augmente la densité des porteurs.
Dans le cas d'une jonction p-n, les électrons et les trous créés dans la zone intermédiaire sont
soumis au champ électrique interne Ein0, lequel déplace les premiers vers la région p et les seconds
vers la région n. Ces déplacements augmentent le courant inverse qui devient I0 + Iph. Le courant
photoélectrique Iph est proportionnel au nombre N de paires électrons-trous créées par seconde (Iph
= −Ne) et donc sensible au flux lumineux Φ qui éclaire la jonction. L'influence de Φ sur le courant
inverse d'une jonction p-n représente l'effet photovoltaique. L'équation de la caractéristique I(U) de
la jonction s'écrit alors :
()
00ph
0
U
IIexp I I
U
=−+
Sur la figure lb, on peut voir la modification de la caractéristique d'une jonction p-n sous l'effet d'un
flux lumineux. Une telle jonction éclairée se comporte alors soit comme un récepteur (quadrants 1
et surtout 3) soit comme un générateur (quadrant 4).
i) Calculer I pour U = −5V, 0V, 0.1V, 0.5V et 5V (I0 = 5 µA et Iph = 5 mA).
a) Photodiode
Une photodiode est une diode à jonction qui travaille en polarisation inverse (U < 0) car c'est dans
le quadrant 3 de la caractéristique que l'influence du flux lumineux est la plus grande (Fig. 1 b).
Pour une tension U < Uo, le courant I vaut :
()
0ph ph
III I−+ − si 0ph II.
Par conséquent, I est proportionnel au flux lumineux Φ. Aussi, lorsqu'on veut comparer des flux
lumineux, utilise-t-on la photodiode dans cette zone de la caractéristique. Notons que l'on a ainsi
réalisé une source de courant commandée par un flux lumineux.
ii) en utilisant le graphique 1b estimer la puissance électrique dans la région du 1er quadrant
limitée entre U∈[0.06 ; 0.1]V et I
∈
[0 ; 5]µA.
b) Cellule photovoltaïque ou photopile
Une jonction p-n éclairée se comporte comme un générateur lorsqu'elle travaille dans le quatrième
quadrant (U > 0 et I < 0). Ce générateur convertit de l'énergie lumineuse en énergie électrique. On
l'appelle cellule photovoltaique ou photopile.
En circuit ouvert (I = 0), on peut voir sur la caractéristique qu'une tension Uph apparaît aux bornes
de la jonction :
()
00ph
0
U
IIexp I I 0
U
=−+= si ph
ph 0 0
I
UUln1
I
=+
.
Cette tension de la photopile est de l'ordre de 0,06V pour une jonction au silicium.
iii) Calculer Iph pour U0 ∼ 25mV et I0 ∼ 5 µA.
Les photopiles sont de plus en plus utilisées pour produire de l'énergie électrique à partir de
l'énergie solaire. L'efficacité de la conversion g
UI
−
⋅
η=
Φ
atteint 0.22 et 0.28 respectivement pour
des photopiles au silicium et à l'arsénure de gallium (GaAs). Les photopiles réalisées actuellement
avec du silicium polycristallin ou amorphe ont des efficacités comprises entre 0.10 et 0.15. Les
valeurs usuelles sont U ∼−1V et I ∼ 1mA.
iv) Calculer les flux lumineux Φ en watt pour les efficacités susmentionnées.