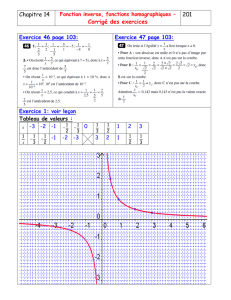
Addition et soustraction de polynômes.

Addition et soustraction de polynˆomes.
On dit que deux expressions alg´ebriques sont semblables si les variables de l’expression
peuvent ˆetre r´eordonn´ees de fa¸con `a ce que la partie des variables soient identiques.
•Par exemple 7x2yz5et 2yx2z5sont des termes semblables puisqu’on peut r´eordonner
les variables comme suit: 7x2yz5et 5x2yz5.
Il est possible d’additionner des termes semblables.
•Par exemple 7x2yz5+ 2x2yz5= 9x2yz5.
•Par contre si les termes ne sont pas semblables il est impossible de les additionner:
l’expression 3x2y+ 5xy2de peut pas ˆetre simplifi´ee et donc doit demeur´ee telle quelle.
Addition de polynˆomes.
L’addition de deux polynˆomes se fait essentiellement qu’en additionnant les termes de
chaque polynˆome qui sont semblables.
•Par exemple, soient les deux polynˆomes
7y3+ 9y2+y+ 5
et
y3+ 2y2+ 4y+ 12.
Pour additionner ces deux polynˆomes il suffit de rassembler les termes semblables des
deux polynˆomes commme suit:
7y3+ 9y2+y+ 5
+y3+ 2y2+ 4y+ 12
8y3+ 11y2+ 5y+ 17
Et donc
(7y3+ 9y2+y+ 5) + (y3+ 2y2+ 4y+ 12) = 8y3+ 11y2+ 5y+ 17
Il faut s’assurer que les termes semblables sont align´es en colonnes.
1

•Par exemple: additionner 2x4−12x2−x+ 12 et x3−2x2+ 3x+ 1.
2x4+ 0x3+−12x2+−1x+ 12
+ 0x4+ 1x3+−2x2+ 3x+ 1
2x4+ 1x3+−14x2+ 2x+ 13
Et donc
(2x4−12x2−x+ 12) + (x3−2x2+ 3x+ 1) = 2x4+x3−14x2+ 2x+ 13
Soustraction de polynˆomes.
Comme l’addition de deux polynˆomes la soustraction se fait essentiellement qu’en soustrayant
les termes de chaque polynˆome qui sont semblables.
•Par exemple, soient les deux polynˆomes
7y3+ 9y2+y+ 5
et
y3+ 2y2+ 4y+ 12.
Pour soustraire le deuxi`eme polynˆome du premier il suffit de rassembler les termes
semblables des deux polynˆomes pour ensuite soustraire chaque terme de la deuxi`eme
ligne du terme correspondant dans la premi`ere ligne comme suit:
7y3+ 9y2+y+ 5
−[y3+ 2y2+ 4y+ 12 ]
6y3+ 7y2+−3y+−7
Et donc
(7y3+ 9y2+y+ 5) −(y3+ 2y2+ 4y+ 12) = 6y3+ 7y2−3y−7
Il faut s’assurer que les termes semblables sont align´es en colonnes.
•Par exemple, pour effectuer la soustraction (2x4−12x2−x+ 12) −(x3−2x2+ 3x+ 1)
on proc`ede comme suit:
2

2x4+ 0x3+−12x2+−1x+ 12
−[ 0x4+ 1x3+−2x2+ 3x+ 1 ]
2x4+−1x3+−10x2+−4x+ 11
Et donc
(2x4−12x2−x+ 12) −(x3−2x2+ 3x+ 1) = 2x4−x3−10x2−4x+ 11
c
Club Pythagore, 2007
3