chap 4 triangle particulier cercle circonscrit

CHAPITRE 4
LES TRIANGLES : CONSTRUCTION AU RAPPORTEUR
TRIANGLES PARTICULIERS et CERCLE CIRCONSCRIT
I Triangle isocèle :
Rappel :
II Triangle équilatéral :
1) Rappel :
2) Remarque :
Les trois angles mesurent tous 60 °
III Triangles rectangles :
1) Construction :
Soit GUS un triangle rectangle en U c'est à dire que GUS est un angle droit.
2) Remarque :
Il existe aussi des triangles rectangles isocèles.
Ils possèdent les propriétés des triangles rectangles et isocèles.
Construis un triangle FBI rectangle isocèle en I tel que
IF = 5 cm et code la figure correctement.
[GS] est l'…hypoténuse……. du
triangle GUS rectangle en U.
B C
A
V I
E
G
US
F
IF
Propriété (admise) :
…si un triangle est isocèle alors il a deux angles de même mesure…
Propriété réciproque (admise) :
……… si un triangle a deux angles de même mesure alors c’est un
triangle isocèle …………
Propriété :
…si un triangle est équilatéral alors il a 3 angles de même mesure…
Propriété réciproque (admise) :
……Si un triangle a 3 angles de même mesure alors c’est un triangle
équilatéral…………………

IV Construction d’autres triangles à l’aide des angles :
Exercices types : Trace les triangles ABC suivants
1er cas : AB = 6 cm , AC = 4 cm et BAC = 70°
2ème cas : BC = 7 cm , ABC = 110° et BCA = 40°
V Utilisation du compas :
Méthode : comment reproduire un angle si on n’a pas de rapporteur ?
a) Nomme le sommet I et un point L et S sur chaque demi-droite
b) Trace une demi droite d’origine I et reporter la longueur de [IL]pour obtenir L
c) Reporte les longueurs de [IS] et [LS] au compas pour obtenir S
d) Trace [IS)
Cela revient à tracer un triangle de même longueur de côtés qu’ ILS
VI Médiatrice et cercle circonscrit :
1) Exercice d’introduction :
a) Kévin et Nicolas ont tous les deux leur arbre fétiche. Ils aiment faire
la course en partant chacun de leur arbre. Place deux points K et N
distants de 4 cm pour représenter leurs arbres.
b) Pour choisir le point d’arrivée de leur course, il faut construire
en bleu l’ensemble des points à égale distance des deux arbres K et N
et y placer un drapeau.
c) Comment se nomme la droite obtenue ? la médiatrice
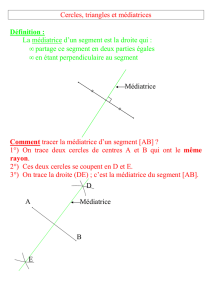
2) Définition de la médiatrice d’un segment :
La médiatrice d’un segment est la droite …perpendiculaire à ce segment en son milieu……….
3) Propriété (admise) :
a) Si un point appartient à la médiatrice d’un segment, alors il est situé à égale distance des extrémités de ce
segment.
b) Réciproquement: si un point est équidistant des extrémités d’un segment, alors il est situé sur la médiatrice
de ce segment.
I
S
L
Passer du tps sur les 2 cas pour la constr. du tri.
"BAC est aigu donc plus petit que l'angle droit."
K N
Arrivée

4) Construction de la médiatrice d’un segment [AB] :
5) Exercice d’introduction suite n°1 :
Nous retrouvons Kévin et Nicolas et le dessin de la partie 1).
d) Gabin a aussi son arbre G et il aimerait faire la course avec Nicolas.
Trace en rouge l’ensemble des points situés à égale distance de Gabin et de Nicolas.
e) Kévin s’ennuie, il propose d’organiser une course à trois.
Où peuvent-ils planter leur drapeau ?
Il faut un point qui soit aussi à la même distance de Kévin et de Gabin
On trace la médiatrice de [KG]
Les trois enfants doivent courir jusqu’au point d’intersection des trois médiatrices.
6) Propriété (admise) :
Les trois médiatrices d’un triangle sont concourantes
1) Construire un triangle BAC.
2) a) Construire D la médiatrice du segment [AB] puis ∆ la médiatrice du segment [CA]. Soit O le point d’intersection des droites D
et ∆ .
b) Démontrer que OA= OB et OA= OC.
3) Démontrer que O appartient à la médiatrice du segment [BC].
4) Que peut-on en conclure?
2) c) On sait que O appartient à la médiatrice de [AB] donc OA=OB.
On sait que O " " " " " " " " [AC] donc OA=OC.
3) On a démontré que OA=OB et OA= AC donc OB=OC. Par suite O est à la même
distance de B et C. donc O appartient à a médiatrice de [BC].
4) O est le point de concours (d'intersection) des trois médiatrices du triangle ABC
de plus OA=OB=OC donc O est le centre du cercle passant par les trois points A,B,C.
7) Exercice d’introduction suite n°2 :
Nous retrouvons Kévin, Nicolas et Gabin et le dessin de la partie 5).
f) Yann n’a pas d’arbre mais il veut courir avec ses camarades.
Nicolas est catégorique : « si tu veux jouer avec nous, ton arbre
doit être aussi loin du drapeau que les nôtres ! ».
Trace l’ensemble des points possibles pour l’arbre de Yann.
Sur un cercle de centre le drapeau et de rayon la distance
du drapeau à l’un des enfants
A
B
A
B
K N
G
arrivéeNG
arrivéeKN
K N
G
K N
G
DD
G
Y

8) Définitions :
Le cercle qui passe par les trois sommets d'un triangle est appelé cercle circonscrit
Le point d’intersection des trois médiatrices est centre du cercle circonscrit
9) Exercices types :
Sur les deux triangles tracés au IV , construis pour chacun les médiatrices des côtés du triangle, puis leur cercle
circonscrit.
10) Remarque :
Il suffit de tracer deux médiatrices pour l’obtenir.
le centre du cercle circonscrit n’est pas nécessairement à l’intérieur du triangle
le cercle circonscrit à un triangle est l’unique cercle qui passe par les 3 sommets de ce triangle
VII Exercice types :
1) Triangle équilatéral :
Trace un triangle équilatéral de côté 5 cm et son cercle circonscrit.
2) Triangle rectangle :
Trace un triangle rectangle de côtés de l’angle droit mesurant 6 cm et 4 cm puis son cercle circonscrit.
Que remarques tu ? Le centre du cercle circonscrit est le milieu de l’hypoténuse.
Repasse AB en rouge et faire
tracer sa médiatrice. Tourner la
feuille et repasse AC en vert et
faire tracer…