tp 2 symetrie

Nom ……………………… 6ème
Prénom ………………………
TP 6 AXES DE SYMETRIE SUR GEOGEBRA
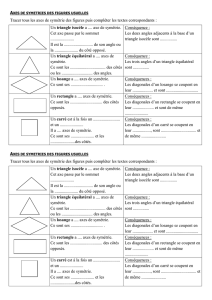
Exercice 1 Axe de symétrie d’un segment
Tracer un segment [AB].
Combien a-t-il d’axes de symétrie ? ………… Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Exercice 2 Axe de symétrie d’un angle
Construire un angle .
Combien a-t-il d’axes de symétrie ? ………… Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Remarque : pour tracer en rouge un objet, utiliser les propriétés de l’objet.
Exercice 3 : Axes de symétrie des triangles
a) Triangle isocèle
Construire un triangle FGH isocèle en H avec FG=5 cm et FH=7 cm.
Combien a-t-il d’axes de symétrie ? ............ Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Calculer avec GEOGEBRA les angles: =............ =............
Que constate-t-on ?
……………………………………………………………………………………….…………………………………….
Compléter les propriétés suivantes :
Si un triangle est ………………, alors ses deux angles à la base ont ………………………………..
Si un triangle est isocèle, alors son axe de symétrie est la …………………… de sa ……….. et aussi
la ……………….. de son angle au …………….. principal.
b) Triangle équilatéral
Construire un triangle IJK équilatéral tel que IJ=4 cm (polygone régulier) .
Combien a-t-il d’axes de symétrie ?............ Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Placer L le point d’intersection des axes de symétrie.
Tracer le cercle de centre L passant par I.
Que constate-t-on ?
……………………………………………………………………………………….…………………………………….
Calculer avec GEOGEBRA les angles: =............ =............ =............
Que constate-t-on ?
……………………………………………………………………………………….…………………………………….
Compléter les propriétés suivantes :
Un triangle équilatéral possède trois axes de symétrie : les ………………………… de ses côtés.
Si un triangle est ……………………., alors ses trois angles ont la même ………………..

Exercice 4 : Axes de symétrie des quadrilatères
Ne pas oublier de tracer à main levée la figure à main levée !
a) Rectangle
Construire un rectangle MNOP avec MN=6 cm et MP=3 cm.
Combien a-t-il d’axes de symétrie ?............ Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Un rectangle possède ………. axes de symétrie : les ………………………… de ses côtés.
b) Losange
Construire un losange QRST avec QR=8 cm et QS=2 cm.
Combien a-t-il d’axes de symétrie ?............ Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Un losange possède ………. axes de symétrie : les ………………………………………………………………….
c) Carré
Construire un carré UVWX avec UV=5 cm.
Combien a-t-il d’axes de symétrie ?............ Le(s) citer et le(s) tracer EN ROUGE sur la figure :
……………………………………………………………………………………….…………………………………….
Un carré possède ………. axes de symétrie : les …………………………………………………………………
…………………………………………………………………………………………………………………………………….