Mouvement parabolique dans un champ de pesanteur

Chapitre 3 : Mouvement parabolique dans un champ de pesanteur uniforme Terminale S
1 / 3
4ème Partie : Evolution temporelle des systèmes mécaniques
Chapitre 3 : Mouvement parabolique dans un champ de pesanteur uniforme.
c.f. TP N° 11 de Physique
Objectifs :
¾ Quelles sont les équations horaires du mouvement ?
¾ Quelle est la trajectoire du centre d’inertie du projectile?
I. Quelles sont les équations horaires du mouvement ?
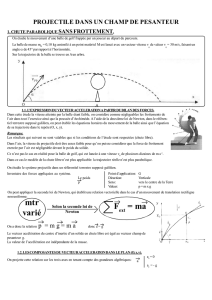
I.1. Bilan des forces extérieures au système
¾ On étudie le lancer d’un projectile avec une vitesse initiale 0 vdans un champ de pesanteur uniforme
(lancer au voisinage de la Terre)
e
nque…)
d’étude est supposé galiléen pour la durée de
ures :
¾ Le système d’étude est un projectile de masse m et d
centre d’inertie G (ex : balle de golf, boule de péta
¾ Le référentiel
O
0
v
i
k
j
α
g
z
x
l’expérience.
¾ Bilan des forces extérie
P- poids du projectile
A
- poussée d’Archimède Π
’air (frottement fluide) : - les forces de frottements de l
f proportionnelle à la vitesse du projectile
On supposera qu’on peut négliger A
et
Π(la masse volumique de l’air est très faible devant celle du projectile)
f (la vitesse initiale du projectile et la distance parcourue suffisamment faibles) devant P.
On pourra donc considérer que le mouvement du projectile est un mouvement de chute libre dans un champ
¾ endant !
y (0) = z (0) = 0
de pesanteur uniforme.
L’axe vertical Oz est asc
¾ A l’instant initial t = 0 s on a x(0) =
Le vecteur vitesse à l’instant initial est 0
v et l’angle de tir est noté (par rapport à l’axe horizontal Ox)
I.2.
α
Coordonnées du vecteur accélération
D’après la deuxième loi de Newton on sait que (t)amP G ⋅= ( est l’accélération du centre d’inertie) (t)aG
soit (t)amgm ⋅=⋅ d’où
G(t)ag = ainsi le vec ra la même direction, le même sens et l
mêm ecteur e pesanteur !
En projetant cette relation selon les trois axes du re
Gteur accélératio a
e valeur que le v champ d
père on obtient les coordonnées du vecteur accélération :
n au
ga
0a
0a =
(t)a
z
y
x
G
−=
=
I.3. Coordonnées du vecteur vitesse
cteur vitesse v¾ Il s’en suit les coordonnées du ve du centre d’inertie du projectile en intégrant les
coordonnées du vecteur accélération on obtient alors :

Chapitre 3 : Mouvement parabolique dans un champ de pesanteur uniforme Terminale S
2 / 3
4ème Partie : Evolution temporelle des systèmes mécaniques
3
2
1
Ctg
C
C
+⋅−=
=
=
z
y
x
v
v
v
v(t) d’après le conditions initiales on en déduit
()
()
αsinvtgv
0v
αcosvv
v(t)
0z
y
0x
⋅+⋅−=+⋅−=
=
⋅==
0z
0x
vtg
v
On remarque que :
- la composante horizontale du vecteur vitesse est constante et vaut
(
)
αcosvv 0x ⋅== 0x v
- la composante verticale du vecteur vitesse est une fonction affine décroissante du temps.
I.4. Equations horaires du mouvement
¾ Il s’en suit les coordonnées du vecteur positionOG du centre d’inertie du projectile en intégrant les
coordonnées du vecteur vitesse on obtient alors les équations horaires du mouvement :
()()
()()
60
2
60z
2
5
4040x
Ctαsinvtg
2
1
Ctvtg
2
1
C
CtαcosvCtv
+×⋅+×⋅−=+×+×⋅−=
=
+×⋅=+×=
z(t)
y(t)
x(t)
OG
D’après les conditions initiales on en déduit les équations horaires :
()()
()()
tαsinvtg
2
1
tvtg
2
1
z(t)
0y(t)
tαcosvtvx(t)
OG
0
2
0z
2
00x
×⋅+×⋅−=×+×⋅−=
=
×⋅=×=
¾ Les coordonnées du vecteur position (équations horaires du mouvement) nous montrent que le mouvement
du projectile est plan, la trajectoire est contenue dans le plan xOz.
¾ La fonction x(t) est une fonction linéaire de coefficient directeur
(
)
αcosv0
⋅
La fonction z(t) est une parabole.
II. Quelle est la trajectoire du centre d’inertie du projectile ?
II.1. Equation de la trajectoire
¾ A l’aide des équations horaires on peut déterminer l’équation de la trajectoire z = f (x).
¾ D’après l’équation horaire tv on peut en déduire que x(t) 0x ×=
()
αcosv
x
v
x
t
00x ⋅
==
En remplaçant l’expression précédente de t dans l’équation horaire z(t) on obtient l’équation de la trajectoire
du projectile :
tvtg
2
1
0z
2×+×⋅−=z(t) donc
() []
() ()
αcosv
x
αsinv
αcosv
x
g
2
1
0
0
2
0
2
⋅
×⋅+
⋅
×⋅−=z(x) en simplifiant on a:
() []
()
αtanx
αcosv
x
g
2
1
z(x) 2
0
2
×+
⋅
×⋅−=
¾ L’équation de la trajectoire est celle d’une parabole (dont la concavité est vers le bas).
¾ On remarque que l’équation de la trajectoire dépend des conditions initiales 0 vet α !

Chapitre 3 : Mouvement parabolique dans un champ de pesanteur uniforme Terminale S
3 / 3
4ème Partie : Evolution temporelle des systèmes mécaniques
II.2. Notions de flèche et de portée
¾ La flèche correspond à la hauteur maximale que peut atteindre le projectile, on la note F (c’est le sommet de
la parabole z(x) ).Voir Fig 3 p 214
Lorsque le projectile atteint la flèche alors la composante verticale de la vitesse en ce point est nulle soit :
()
0αsinvtgv 0Fz
=
⋅+⋅−= soit l’instant où le projectile est à sa hauteur maximale est :
F
t
(
)
g
αsinv
t0
F
⋅
=
et donc la hauteur maximale z(flèche) aura pour expression :
F
()()
(
)
(
)
g
αsinv
g
αsinv
g
2
1
tαsinvtg
2
12
2
0
2
2
2
0
F0
2
F
⋅
+
⋅
×⋅−=×⋅+×⋅−=)z(tF ce qui donne après
simplification :
()
g
αsinv
2
1
)z(t 0
F
⋅
⋅= 2
2
¾ La portée correspond à la distance maximale que peut atteindre le projectile, on la note P (c’est le point
d’intersection du projectile avec l’axe horizontal Ox qui correspond souvent au sol) Voir Fig 3 p 214
Lorsque le projectile atteint le point P alors 0)z(xP
=
ainsi cela revient à résoudre une équation du second
degré :
()
[]
()
0αtanx
αcosv
x
g
2
1
P
2
0
2
P=×+
⋅
×⋅−=)z(xP soit
() ()
0αtan
αcosv
x
g
2
1
x2
2
0
P
P=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+
⋅
×⋅−×=)z(xP
Les deux solutions analytiques sont :
- mais cela n’a aucun intérêt physique !!!
0xP=
-
() ()
g
αtanαcosv2
x
2
2
0
P
×⋅⋅
= ce qui donne par simplification
()
g
2αsinv
x
2
0
P
⋅
=
(car
() ()
()
αcos
αsin
αtan = et
() ()
(
)
2αsinαcosαsin2
=
⋅
⋅
)
II.3. Influence des conditions initiales sur la trajectoire
¾ Pour une même valeur de vitesse initiale v0, l’angle de tir α a une importance sur la flèche et la portée.
La portée sera maximale lorsque l’angle de tir est α = 45° (car sin (2α) = 1 et donc g
v
x
2
0
P=)
α
1 >
α
2 >
α
3
et
v0 est constant
z
x
α2
α1
α
3
z
x
¾ Pour une même direction (même angle de tir), plus v0 est grand, plus la flèche et la portée seront
importantes. Figure 4 B p 215 (attention dans ce cas on ne pourra plus négliger les frottements de l’air).