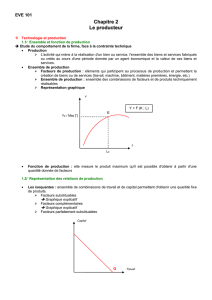
La productivité marginale

1
Chapitre 4: Les choix du producteur
Les types de technologie de production
Introduction
Fonction de production linéaire
Fonction de production Leontief
Fonction de production Cobb-Douglas
Différents concepts liés à la technologie de production
Le taux marginal de substitution technique (TMST)
La productivité marginale
Les rendements d’échelle
Le court et le long terme pour un producteur
Les profits et les coûts de production
Le profit
Les coûts
Le problème de la firme
La fonction de coût
La fonction de coût à court terme
La fonction de coût à long terme

2
Les types de technologie de production
Introduction
De façon schématisée, voici comme fonctionne la production
VOIR FIGURE 4.1
Le choix optimal du producteur se rapportera à la quantité optimale d’inputs à utiliser. Dans le
cas d’une concurrence pure et parfaite (CPP), ce choix dépendra des prix des inputs et des
outputs ainsi que du type de technologie de production.
Supposons que le producteur utilise
I
inputs pour produire
J
outputs
1,...,
inputs i I
⇒=
1,...,
outputs j J
⇒=
Supposons que la production de chaque produit (output) est caractérisée par un type de
technologie notée
f
(
f
pour fonction de production)
1 1 1
1
1
( ,..., )
...
( ,..., )
...
( ,..., )
I
j j I
J J I
q f x x
q f x x
q f x x
=
=
=
où
j
q
est la quantité de biens
j
produite,
i
x
est la quantité de facteurs de production
j
nécessaire à la production de
j
q
et
j
f
est la technologie de production utilisé pour produire le
bien
j
.
Notons qu’il est possible que le producteur utilise la même technologie pour produire
différents produits.

3
Sans perte de généralité, concentrons-nous sur une économie caractérisée par 2 inputs (
2
I
=
)
et 1 ouput (
1
J
=
). Par exemple
( , )
q f L K
=
Fonction de production linéaire
Cette technologie de production est caractérisée par le fait que les inputs sont parfaitement
substituables entre eux de sorte que la fonction de production est donnée par
1 2 1 2
( , )
q f x x a x b x
= = ⋅ + ⋅
Supposons que
a b
=
. Graphiquement, cela donne
VOIR FIGURE 4.2
Fonction de production Leontief
Cette technologie de production est caractérisée par le fait que les inputs sont parfaitement
complémentaires entre eux de sorte que la fonction de production est donnée par
1 2 1 2
( , ) min( , )
q f x x a x b x
= = ⋅ ⋅
Pour faciliter la compréhension de ce type de technologie de production, supposons que
q
est
la quantité de tasses de café,
1
x
la quantité de café et
2
x
la quantité d'eau. Graphiquement,
cela donne
VOIR FIGURE 4.3
où
1
q
,
2
q
et
3
q
représentent différents niveaux de production (
3 2 1
q q q
> >
).

4
Fonction de production Cobb-Douglas
Cette technologie de production est caractérisée par le fait que les inputs ne sont ni
parfaitement substituables, ni parfaitement complémentaires. On dit simplement que les input
sont (imparfaitement) substituables de sorte que la fonction de production est donnée par
1 2 1 2
( , )
q f x x A x x
α β
= = ⋅ ⋅
où
A
est la taille de la production (facteur de productivité totale),
α
et
β
sont des
paramètres qui régissent la réactivité de l’output
q
à des changements de quantité d’inputs
1
x
et
2
x
, respectivement. Plus précisément
1 2
1
ln ( , )
ln
f x x
x
α
∂
=∂ est l’élasticité output-input
1
x
1 2
2
ln ( , )
ln
f x x
x
β
∂
=∂ est l’élasticité output-input
2
x
Graphiquement, on a
VOIR FIGURE 4.4
Sur ce graphique est représentée une isoquant qui nous donne l’ensemble des combinaisons
1 2
( , )
x x
tel que la quantité produite est donnée par
1 2
( , )
q f x x
=.
→ les propriétés de l’isoquant sont les suivantes
• les isoquants ne se coupent jamais
• elles ont une pente négative
• plus on s’éloigne de l’origine des axes, plus le niveau de production augmente

5
Différents concepts liés à la technologie de
production
Le taux marginal de substitution technique (TMST)
Le taux marginal de substitution technique (TMST) nous donne la quantité d’inputs 2 à la
quelle le producteur doit renoncer lorsqu’il augmente la quantité d’inputs 1 de façon
infinitésimale tel que le niveau de production reste constant. Formellement il est donné par
1 1
2
1
x x
dx
TMST dx
=
= −
En d’autres termes, il nous donne la pente de l’isoquant lorsque la quantité d’inputs 1 utilisée
est
1 1
x x
=
.
La productivité moyenne de l’input
i
est la quantité produite par unité d’input
i
.
Formellement il est donné par
1 2
( , )
( 1,2)
ii
f x x
PM i
x
= =
La productivité marginale de l’input
i
est la variation de la quantité produite lorsque la
quantité d’inputs
i
varie de façon infinitésimale (variation marginale de
i
x
). Formellement il
est donné par
1 2
( , )
( 1,2)
ii
f x x
Pmg i
x
∂
= =
∂
Ayant en tête la définition du TMST faite ci-dessus, nous pouvons réécrire le TMST de la
façon suivante