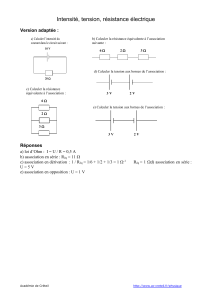
Associations de résistances

Prévoir une calculatrice
scientifique : par exemple
la LEXIBOOK
1 . Résistances en série
LOI : La résistance équivalente à plusieurs résistances en série est égale à leur somme
Exemple Réq = R1 + R2 Réq = R1 + R2 + R3
Question examen 1 :
R1 et R2 sont en série .On connaît l'in
tensité dans la série et la tension aux bor
nesde cette série . On peut donc calculer
la résistance totale de la série avec la
loi d'Ohm :
très simple Rtot = U / i = 10 V / 0,020 A = 500 ohms
Donc R1 = 500 - 100 = 400 ohms
( inutile de calculer U1 et U2 )
Question examen 2
On demande i dans la série . C'est le même dans R1 et R2 .
On peut calculer U1 , la tension sur R1
U1 = 5 - 2 = 3 V
Avec U1 et R1 on peut calculer i ( loi d'Ohm )
i = U1 / R1 = 3 V / 3 000 ohms = 0,001 A = ..? ... mA
( on pourrait trouver maintenant R2 . ........ ? )
2 . Résistances en parallèle .
On admet la loi suivante :
LOi : La résistance équivalente à 2 résistances R1 et R2 en parallèle est telle que :
1
Réq =1 R1 1 R2
A retenir ou
Réq=R1∗R2
R1R2
Pour 3 résistances R1 , R2 , R3 on a
1
Réq =1 R1 1 R2 1 R3
A retenir
Exemple 1 . Soit 2 résistances de 6 ohms et 3 ohms en parallèle . Quelle est la résistance
équivalente ?
On a donc
1
Réq =1 61 3
A la calculatrice on tape 1 : 6 + 1 : 3 = On trouve 0,5 qui est donc 1 / Réq c'est à dire
l'inverse de Réq ( L'inverse d'un nombre x c'est 1 / x ) Sur la calculatrice Lexibook
l'invers de x est obtenu avec la touche x-1 .
On a donc
1
Réq =0,5
Pour obtenir Réq il suffit de prendre l'inverse de 0,5 soit 1: 0,5 =
On trouve 2 ohms .
A la calculatrice , pour calculer Réq , il suffit de taper successivement :
1/6 + 1/3 = x-1 = Réponse 2 ohms Faire la manipulation . ( 2 est inférieur à 3 )
Il revient au même de taper successivement :
6 x-1 + 3 x-1 = x-1 = Faire la manipulation
Associations de résistances
R1 R2 R1 R2 R3
I = 20 mA
U1 U2
10 V
R1 = ?? R2=100Ω
I = ??
R1 = 3 kΩ
R2
5 V
2 V
R1
R2
Réq ??
10 Ω
20 Ω
5 Ω

On peut aussi utiliser la touche "fraction" ab/c sur la Lexibook .
1 ab/c 6 + 1 ab/c 3 = 1 / 2 Donc 1/ R = 1 / 2 En prenant l'inverse R = 2
Exemple 2
Résistance équivalente à 10 , 2 et 5 ohms en parallèle .
1
Réq =1 10 1 21 5
Faire le calcul de 3 façons comme pour l'exemple 1 .
Ecrire le calcul puis le taper . On utilise la touche x-1 4 fois
Avec la touche fraction ab/c : 1ab/c10 + 1ab/c2 + 1ab/c5 = 4 / 5 ( le faire )
D'où 1 / R = 4 / 5 . En prenant l'inverse des 2 côtés R = 5 / 4 = 5 : 4 = 1 , 25
Réponse : 1,25 ohm qui est inférieur à la plus petite des résistances .
Question examen 3
Quelle résistance faut-il mettre en // avec une résistance de 1 000 Ω pour obtenir 800 Ω ?
On cherche donc la résistance x telle que
1
1000 1 x=1 800
.
Cette égalité ou équation est du type a + x = b , x étant l'inconnue et a et b des nombres
connus .
Si l'on retranche a des 2 côtés du signe = on a une autre égalité :
a + x - a = b - a ou x = b - a
Avec 1 /1 000 + 1/x = 1/800 on btient 1 / x = 1/ 800 - 1/ 1 000 = 0 , 000 25
On doit maintenant prendre l'inverse de 0 , 000 25 en tapant 0,000 25 x -1 =
Résultat 4 000 ohms . Faire la vérification .
Finalament pour trouver x il suffit de taper successivement :
800 x -1 - 1 000 x -1 = x -1 = Faire la manipulation
ou bien
1 / 800 - 1 / 1 000 = x -1 = Faire la manipulation
Remarque : on prendra une résistance normalisée de 3 900 ohms
Autre exemple
Chercher la valeur de la résistance à mettre en parallèle avec 240 ohms pour obtenir 140
ohms .
On doit trouver 336 ohms ( donc pratiquement 330 normalisé )
Cas où les résistances en // sont identiques
On a
1
Réq =1 R1 R1 R
ou
1
Réq =111 R=3 R
En prenant les inverses aux 2 bouts :
Réq
1=R 3ou Réq=R 3
La résistance est divisée par 3 .
Si l'on a n résistances de R ohms en parallèle , la résistance équivalente est :
Réq=R
n
ou Réq = R / n A retenir
Question examen 4
Combien faut-il de résistance de 1 000 ohms en // pour obtenir une résistance de 50 ohms .
Cela permet de réaliser une charge fictive . Solution en page 4.
R R R Réq

Question examen 5 Résistance du dipôle AB ?
A QCM
A ) 60 Ω B ) 20 Ω C ) 15 Ω D ) 10 Ω
10 et 10 en série donne ......
20 et ..... en // donne ........
B ......... ..............
Toutes valeurs en ohms Solution en page 4
3 . Pont de Wheatstone
C'est un dispositif à 4 noeuds A , B , C , D qui permet de mesurer des résistances . Avec les
progrès de l'électronique il n'est plus utilisé mais le montage en pont existe toujours . Il sert
pour d'autres mesures .
Pou une fois voyons comment on trouve la résistance inconnue X .
On fait varier R2 pour obtenir un courant nul entre B et D . Alors la tension UBD est nulle .
On dit que le pont est à l'équilibre .
On a UBA = UBD + UDA
0
Donc UBA = UDA
E étant la tension aux bornes de la pile et
aussi aux bornes de ABC ou (R1 + R2) et
ADC ou (R4 + X ), on peut exprimer UBA ,la
tension sur R1 et UDA , la tension sur R4 , en
fonction de E et des 4 résistances :
UBA =
E∗R1
R1R2
UDA =
E∗R4
R4x
Comme les 2 tensions sont égales on peut
écrire
E∗R1
R1R2=E∗R4 R4X
On peut diviser par E des 2 côtés du signe = . Il reste alors :
R1
R1R2=R4 R4x
Ecrivons que les prosuits en croix sont égaux :
R1 * ( R4 + X ) = R4 * (R1 +R2)
Effectuons les 2 produits en suivant les flèches : R1 * R4 + R1 * X = R1 * R4 + R2 * R4
Le produit R1 * R4 figure des 2 côtés du signe = . Nous pouvons le supprimer . Nous
obtenons une nouvelle égalité :
R1 * X = R2 * R4 A retenir
On observe que R1 et X sont en face l'un de l'autre sur le pont ; même remarque pour R2
et R4 .
La dernière égalité est une équation d'inconnue X . Si l'on a par exemple 3 * X = 15 on
en tire X = 15 / 3 = ......?.... en divisant par 3 des 2 côtés du signe = .
Ici on obtient
X =
R2∗R4
R1
20
10
10
20
30 Réq ??

Question examen 6
Le galvanomètre G n'indique aucun courant
Calculer X dans ce circuit .
solution en page 4
Toutes valeurs en ohms
Corrigé des exercices
no 4
La résistance équivalente est 50 ohms obtenue avec des résistances de 1 000 ohms .
Formule de la page 2:
Réq=R
n
On cherche n .
On a donc
50=1000
n
ou encore
50
1=1000 n
Faisons les produits en croix
50 * n = 1 * 1 000 = 1000 D'où n = 1 000 / 50 = 20 résistances
no 5
On peut simplifier progressivement le schéma donné
10 et 10 en série donne 20
20 et 20 en // donne 10
20 et 10 en série donne 30
30 et 30 en // donne 15 Réponse C
no 6
On reconnaît un pont de Wheatstone
En faisant les produits des résistances en diagonale
100 * X = 300 * 200 ( équation d'inconnue X)
X =
300∗200
100
. Il reste
X=300∗2
1=600 ohms
Autres exercices
Exprimer la résistance des dipôles AB en fonction de r
voir page 5
100 200
300 X
10 V G

Pour calculer simplifier progressivement les schémas