Objectif Bac Mécanique de Newton p. 217

TISSERAND Correction DM n°4 Terminale S
1
Objectif Bac Mécanique de Newton p. 217
1. Fiche Technique d’une automobile
A. analyse des informations
1. a) Le poids est une force exprimée en Newton (N). La masse s’exprime en kg.
b) La puissance s’exprime en Watts (W) en unités SI.
2. L’accélération au sens physique peut-être positive ou négative. Les rubriques sont donc : Accélérations,
Reprises et Freinage.
A. Etude scientifique
1. a) cf. cours.
b) Dans la rubrique Reprises on peut calculer ΔV = Vfinal-Vinitial, donc a = ΔV/ treprise.
2. a) Si a est constante alors V(t) = a.t + V0 avec V0 = 0 m.s-1. Donc V(t) = a.t
b) V(t) = dx/dt donc x(t) = ½ .a.t2 + x0 avec x0 = 0 m. Donc x(t) = ½ .a.t2.
c) a1 = 2.x1 / t12 = 2.52 m.s-2 et a2 = 2.x2 / t22 = 1.89 m.s-2
a1 < a2 car les frottements mécaniques augmentent si la vitesse augmente.
3. a) V(t) = a.t + V0 avec V0 = constante.
b) Donc en reprise, a = (V- V0)/ treprise soit a(4ième) = 1,06 m.s-2 et a(5ième) = 0,68 m.s-2 .
le moteur est moins nerveux en 5ième vitesse.
4. a)
( ) ( )
( ) ( )
( ) ( )
12
2
1
2
2
2
1
2
2
2
1
2
212
2
1
2
2
2
2
1
2
2
2
1
22
1
2
2
22
2
..2)()(
)()(
.2
1
..
2
1
)()(
1
.)(
.)(
xxatVtV
tVtV
a
ttaxx
tVtV
a
ttdonc
tatV
tatV
!=!
!=!=!
!=!
"
#
"
$
%
=
=
Finalement :
( )
12
2
1
2
2
.2
)()(
xx
tVtV
a
!
!
=
b) On remplace par les valeurs de freinage avec V(t2) = 0 m.s-1.
On obtient : a1 = 113 m.s-2
a2 = 119 m.s-2
a3 = 126 m.s-2
c) Système : la voiture
Référentiel : terrestre (galiléen)
Bilan des forces : poids, réaction, force de freinage
2nde loi de Newton :
amFRP r
rrr
.=++
Avec
0
r
rr
=+ RP
car le mouvement s’inscrit dans le plan horizontal.
On projette sur l’axe Ox : F = m.a
Donc : F1 = 1,06 .104 N
F2 = 1,16 .104 N
F3 = 1,22 .104 N
Si F3 > F2 > F1 alors les frottements aérodynamiques ne peuvent plus être négligés à grande
vitesse.

TISSERAND Correction DM n°4 Terminale S
2
d) Théorème de l’énergie cinétique entre les points A et B : ΔABEcinétique = WP/AB + WR/AB + WF/AB
avec WP/AB = WR/AB = 0 J. car les forces sont perpendiculaires au déplacement AB.
Donc Ecin(B)- Ecin(A) = -F.AB avec Ecin(B) = ½. m.VB2 = 0 J.
Soit
AB
Vm
AB
E
FA
Acin
.2
.2
)( ==
2. Distance de freinage d’une automobile
1. Le mouvement est rectiligne décéléré.
2. a) Système : voiture
Référentiel : terrestre (galiléen)
Bilan des forces : poids, réaction et force de freinage
2nde loi de Newton :
amFRP r
rrr
.=++
Avec
0
r
rr
=+ RP
car le mouvement s’inscrit dans le plan horizontal.
Donc :
amF r
r
.=
b) la vitesse moyenne s’exprime par Vmoyenne = D/Δt
et d’après l’énoncé : Vmoyenne = (Vfinale+Vinitiale)/2 = (0+Vinitiale)/2
Donc : Δt = 2D / Vinitiale
Valeurs numériques :
Vinitiale (m.s-1)
Δt sèche (s)
Δt mouillée (s)
12,5
2,08
4,16
25,0
4,16
8,32
36,0
6,83
13,7
c) a = (Vfinale-Vinitiale)/ Δt = (0 -Vinitiale)/ Δt < 0
car l’accélération est opoosée au sens du mouvement pour décélérer le système.
Vinitiale (m.s-1)
a sèche (m.s-2)
a mouillée (m.s-2)
12,5
-6,01
-3,00
25,0
-6,01
-3,00
36,0
-5,27
-2,63
d) A grande vitesse, la valeur absolue de l’accélération diminue car on ne peut plus négliger les
frottements aérodynamiques.

TISSERAND Correction DM n°4 Terminale S
3
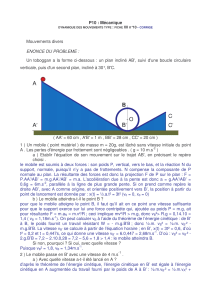
3. Etude du dépassement de 2 mobiles
1. Le solide I est derrière le solide II jusqu’à la position 14. Le dépassement a lieu entre les positions 14 et
15, donc entre les instants t14 = 14 × 0,02 = 2,8 .10-1s et t15 = 15 × 0,02 = 3,0 .10-1s
2. On trace les graphes suivants :
y = 38.382x + 10.043
y = 70.926x - 0.0265
-5
0
5
10
15
20
25
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35
t (s)
x I (10-2 m) x II (10-2 m)
Linéaire (x II (10-2 m)) Linéaire (x I (10-2 m))
La date du dépassement se situe à l’intersection des deux droites aux alentours de 3,0 .10-1s pour une
distance parcourue environ égale à 2,1 .10-1m.
3. Les mouvements sont rectilignes uniformes car les mobiles ne sont soumis qu’à des forces qui se
compensent (poids et réaction).
Donc
!
"
#
+=+=
+=+=
10,0.)0(.
0.)0(.
2222
1111
tVxtVx
tVxtVx
car x2(0) = 10 cm = 0,10 m
Donc : V1 = pente de la droite x I (t) = 7,1.10-1m.s-1
V2 = pente de la droite x II (t) = 3,9.10-1m.s-1
On cherche la date du dépassement pour une distance parcourue x :
39,0
10,0
71,0
10,0
21
!
==
!
==
xx
t
V
x
V
x
t

TISSERAND Correction DM n°4 Terminale S
4
Donc x = 2,22 .10-1m. et t = 0,31 s.
4. a) Système : Solides I et II.
Référentiel : Terrestre (galiléen).
Mouvement : rectiligne uniforme.
Bilan des forces : poids et réaction.
Comme la vitesse est constante, la variation d’énergie cinétique est nulle : ΔEcinetique = 0 J.
On retrouve d’après le théorème de l’énergie cinétique : WP/AB + WR/AB = 0 J.
Car WP/AB = WR/AB = 0 J. Le poids et la réaction sont perpendiculaires au déplacement AB.
L’énergie est conservée pour le système Solides I + II
b) Système : solide I.
Mouvement : la vitesse diminue après la solidarisation donc Vfinale < Vinitiale
D’après le théorème de l’énergie cinétique :
ΔEcinetique = ½ mVfinale2 - ½ mVinitiale2 < 0 J.
Comme on a toujours WP/AB = WR/AB = 0 J. Le poids et la réaction sont perpendiculaires au
déplacement AB.
On obtient : ΔEcinetique ≠ WP/AB + WR/AB
Le théorème de l’énergie cinétique n’est pas vérifié. L’énergie n’est pas conservée pour le solide I.
c) Système : Solide II.
Mouvement : la vitesse augmente après la solidarisation donc Vfinale > Vinitiale
D’après le théorème de l’énergie cinétique :
ΔEcinetique = ½ mVfinale2 - ½ mVinitiale2 > 0 J.
Comme on a toujours WP/AB = WR/AB = 0 J. Le poids et la réaction sont perpendiculaires au
déplacement AB.
On obtient : ΔEcinetique ≠ WP/AB + WR/AB
Le théorème de l’énergie cinétique n’est pas vérifié. L’énergie n’est pas conservée pour le solide II.