Travail des forces au cours d`un mouvement de translation rectiligne

1
Travail et énergie cinétique
1er exercice. Définitions.
1. Calculer l’énergie cinétique de translation d’une automobile de masse m = 1200 kg roulant à la vitesse
v = 90 km.h-1.
2. Exprimer et calculer la vitesse d’un électron de masse m = 9,1.10-31 kg possédant l’énergie cinétique
Ec = 500 eV. Donnée. 1 eV = 1,60.10-19 J.
3. Un voyageur, de masse m = 70 kg, dans un train, marche vers l’arrière du véhicule à la vitesse
constante v = 2 m.s-1. Le train roule en ligne droite à la vitesse constante vT = 25 m.s-1.
Calculer l’énergie cinétique de translation du voyageur :
a. dans le référentiel du train. b. dans le référentiel terrestre.
2ème exercice. Chute verticale dans l’air.
Un pot de fleurs de masse m = 2 kg tombe de la fenêtre
d’un appartement du 3ème étage d’un immeuble, située à la
hauteur H = 10 m au dessus du sol. Le solide est lâché sans
vitesse initiale, nous noterons G0 la position de son centre
d’inertie. Au point G, tel que G0G = h, la vitesse de son
centre d’inertie est v.
1. Dans un premier temps, on néglige la résistance de l’air.
a. A quelle(s) force(s) est soumis le solide ? Représenter
cette (ou ces) forces.
b. En appliquant le théorème de l’énergie cinétique, exprimer, en fonction de g et h, la vitesse atteinte
par le solide au point G. En déduire une autre unité pour la constante de pesanteur g.
c. La vitesse atteinte dépend-elle de la masse du solide ? Conclure.
d. Enoncé, en commun, avec le vocabulaire adapté, des lois de Galilée concernant la chute libre.
e. Application numérique. L’accélération de la pesanteur est g  9,8 m.s-2.
Calculer la vitesse du mobile à son arrivée au sol, en m.s-1 et en km.h-1.
f. Construire un diagramme des échanges énergétiques.
2. En fait, compte tenu de la résistance de l’air, l’énergie cinétique du solide à son arrivée au sol est égale
aux 2/3 de sa valeur théorique. La force de frottement
f
est supposée constante et colinéaire au vecteur
vitesse.
a. Faire le bilan des forces appliquées au solide. Déterminer la valeur de la force de frottement.
b. Construire un nouveau diagramme des échanges énergétiques.
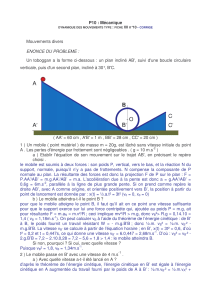
3ème exercice. Satellite géostationnaire.
Un satellite géostationnaire est toujours sur une orbite circulaire, centrée
au centre de la Terre et située dans le plan de l’équateur.
Le rayon de l’orbite est fixé : r  42150 km.
Données.
Le rayon moyen de la Terre : RT = 6370 km. La masse de
la Terre : MT  6.1024 kg.
Constante de gravitation : G = 6,67.10-11 N.m2.kg-2.
Le jour sidéral, période de rotation de la Terre dans le référentiel géocentrique : 1 j  86164 s.
1. Quelle est le mouvement d’un tel satellite dans le référentiel terrestre ? Déterminer son altitude z.
2. Compléter le schéma en faisant apparaître la force subie par le satellite. Calculer cette force pour un
satellite de masse m = 1 tonne.
3. Déterminer dans le référentiel géocentrique le sens du mouvement du satellite.
4. Montrer que, dans ce référentiel, le mouvement du satellite est uniforme :
a. par une méthode dynamique (utilisant les lois de Newton)
b. en utilisant le théorème de l’énergie cinétique.
5. Déterminer la période de révolution T, la vitesse angulaire  et la vitesse du satellite v. Représenter
v
.
G0
h
G
H

2
4ème exercice. Travail des forces au cours d’un mouvement de translation rectiligne uniforme.
Examinons, sous un nouvel angle, le problème déjà rencontré du skieur sur un remonte-pente.
Sa masse est m = 70 kg. Il est tiré par la perche d’un téléski à vitesse constante v = 5,0 m.s-1.
La piste est plane et inclinée d’un angle  = 20° par
rapport à l’horizontale.
La direction de la perche fait un angle  = 30° par
rapport à la piste.
Les frottements sont équivalents à une force constante
f
, colinéaire au vecteur vitesse et de valeur f = 100 N.
On donne g = 9,8 N.kg-1.
1. Faire le bilan des forces appliquées au skieur.
2. Considérons un déplacement d’amplitude AB = l.
Exprimer, en fonction des données utiles, les travaux du poids
P
du skieur, de la réaction normale
R
de
la piste, de la force de frottement
f
et de la tension
T
de la perche.
3. Sachant que le skieur est animé d’un mouvement de translation rectiligne uniforme, exprimer puis
calculer la valeur T de la tension de la perche.
4. Calculer la valeur de la puissance P développée par la tension
T
.
5ème exercice. Les oscillations du pendule.
Un pendule simple est constitué d'un solide ponctuel de masse m = 100 g suspendu à un fil inextensible et
sans masse de longueur l = 0,30 m.
L'accélération de la pesanteur est g  10 m.s-2.
On suppose négligeables les frottements.
L'expérimentateur écarte le pendule de sa position d'équilibre d'un angle
0 = 45° et le lâche sans vitesse initiale.
1. Le pendule faisant avec la verticale l'angle , faire le bilan des forces
auxquelles est soumis le solide. Représenter également le vecteur
vitesse au point G.
2. Exprimer, en fonction des données, le travail du poids et de la tension
du fil :
a. entre les points G0 et G.
b. entre les points G0 et G1.
3. En appliquant le théorème de l’énergie cinétique, établir l’expression
littérale de la vitesse v1 en G1. Calculer sa valeur.
6ème exercice. Plan incliné.
Un solide ponctuel, de masse m = 500 g, glisse le long d’un plan
incliné d’un angle  = 20°.
Au point O, d’abscisse 0, sa vitesse est v0 = 2,1 m.s-1.
Au point M, d’abscisse x, sa vitesse est v.
Accélération de la pesanteur : g = 9,8 m.s-2.
1. Définir le référentiel d’étude.
2. Hypothèse du mouvement sans frottements.
a. Faire le bilan des forces.
b. En appliquant le théorème de l’énergie cinétique, exprimer v en fonction de v0, g et .
La vitesse v dépend-elle de la masse ?
c. Calculer v pour x = 1,20 m.
3. En réalité v = 2,9 m.s-1. Justifier.
Exprimer, puis calculer, la valeur f de la force de frottement, supposée constante, responsable de cette
différence.
 = 20°
O
M (x)
i
j
O
O
G1
G
G0
+
0