Solides en mouvement

Solides en mouvement
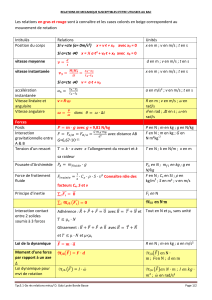
I) Principe fondamental de la dynamique appliquée au solide :(système indéformable)
I.1) Principe des actions réciproques ou 3ème loi de Newton:
Lorsque un système S exerce une force
'SS
F
sur un système S’, le système S’ exerce au
même instant une force
'
'SS F
sur S. Ces deux forces ont même droite d’action et vérifient
la relation
''S S S S
FF
R
P
I.2) Exemple de forces :
Poids d’un objet
Poussée d’Archimède
Tension d’un ressort
Frottements
P mg
2
N kg m s
ao
P Vg
3 3 2
N kg m m m s
Poids du volume d’eau déplacé
.T k l
1
N N m m
K raideur du ressort
l
élongation
Les frottements sont
donnés
tan
S
frot
fR
NN
P
0Vg
P
R
f
P
I.3) Deuxième loi de Newton :Principe fondamental de la dynamique.
Dans un référentiel galiléen la somme des forces extérieures appliquées à un solide est égale au produit de la masse
du solide par l’accélération de son centre d’inertie.
G
F ma
Unités F en N , a en m.s-2,m en kg.
GG
Gdv v
adt t
et
GdOM
vdt
OM
vecteur
position du solide dans un repère
, , ,O i j k
L’expression générale du mouvement d’un solide
uniformément accéléré est
2
()
1
() 2
initiale
initiale initiale
v t a t v
d t a t v t d
I.4) Couple exercé par une force sur un axe:
O un point de l’axe .
C OM F
sinC OM F
r en m ; F en N ; C en N.m.
O
F
M
r
sinF
I.5) Moments d’inertie:
Le moment d’inertie quantifie la résistance d’un corps à la mise en rotation, comme les masses ils
s’ajoutent.
2
ii
i
J m r
pour un cylindre
2
1
2
J MR
(unité : kg.m²)
I.6) Principe fondamental de la dynamique des systèmes en rotation :
d
CJ
dt
Unités: C en N.m, J en kg.m2,
dt
d
en rad.s-2
dt
d
vitesse angulaire en rad.s-1 et
2
2
dt
d
dt
d
accélération angulaire en rad.s-2
R
M

I.7) Transmission des couples :
Couple transmis : L’énergie est conservée sur chaque pièce en rotation :
1 1 1 2 2 2
P C P C    
Rapport de transmission d’un engrenage :
Rapport de transmission :
1 2 2 1
2 1 1 2
CR
CR
Si le rendement de la transmission est a comptabiliser, il se répercute sur le
couple :
21
2 1 1 2 2
1 1 1
22
PP
P C C
CC
C
II) Aspect énergétique :
II.1) Travail, puissance, rendement:
II.1.1) Expression du travail d’une force constante :
. . .cos
AB
W F AB F d
avec d=AB norme déplacement, angle entre
F
et le vecteur déplacement.
II.1.2) Expression du travail d’un couple constant :
Le travail d’un couple constant C se déplaçant de l’angle  est égal au produit de C par .
WC
avec W en J ;  en radian ; C en N.m.
II.1.3) Puissance développée par un couple C:
.P F v
P=F .v cos P en W; F en N ; v en m.s-1.
II.1.4) Puissance développée par un couple C :
PC 
avec P en W ; C en N.m ;  en rad.s-1.
II.1.5) Rendement:
uu
aa
PW
PW
<1 Pa=Pu+pertes.
II.2) Energie :
II.2.1) Energie cinétique :
Solide en translation rectiligne :
2
1
2
C
E m v
avec EC en J ; m en kg ; v en m.s-1.
Solide en rotation par rapport à un axe fixe:
2
1
2
C
EJ 
avec EC en J ; J en kg.m2 ;  en rad.s-1.
II.2.2) Théorème de l’énergie cinétique :
12
12C C ext
E E W F 
ou
()
ext
dEc PF
dt 
II.2.3) Energie potentielle :
Energie potentielle de pesanteur :
2 1 2 1pp
E E mg z z  
Avec EP en J ; m en kg ; z en m.
Energie potentielle élastique :
21
22
21
1
2
pp
E E k x x    
EP en J ; k en N.m-1. ; x en m.
Ressort de torsion :
21
22
21
1
2
pp
E E k
EP en J ; k en N.m.rad-1. ;  en rad.
II.2.4) Energie mécanique :
L’énergie mécanique d’un système énergétiquement isolé est égale à la somme de son énergie potentielle et de son
énergie cinétique.
L’énergie mécanique se conserve donc:¨
te
M C P
E E E C  
Un système est énergétiquement isolé s’il n’échange aucune énergie avec le milieu extérieur.
R
v
R
1
2
R1
R2
F2
F1
R2
R1
R1
R2
1=2
F2
F1
F2
F1
F1 =F2
v1=v2
12
C1C2
P=Fv=C11= C22
F1 =F2
v1=v2
12
C1C2
P=Fv=C11= C22
1=2
C1=C2
F1 F2
v1v2
P= C=F1v1=F2v2