FORCES ÉLECTROMAGNÉTIQUES - exercices A. EXERCICES DE

1
FORCES ÉLECTROMAGNÉTIQUES - exercices
A. EXERCICES DE BASE
I. Fréquence cyclotron
• Une particule “ponctuelle” de charge q et de masse m est placée dans une région de lʼespace où
règne un champ magnétique uniforme
!
B
dirigé selon lʼaxe Oz. Cette particule subit la force de Lorentz
!
F
=
=
!
qv "B
(où
!
v
désigne sa vitesse dans le référentiel correspondant au repère Oxyz utilisé).
• En négligeant le poids de la particule, montrer que vz est constante, puis que la projection de la
trajectoire sur le plan Oxy est décrite avec une période qui ne dépend que de q, m et B.
• Déterminer les expressions de x(t) et y(t) pour les conditions initiales :
x(0) = x0 ; y(0) = 0 ; x•(0) = 0 ; y•(0) = v0y.
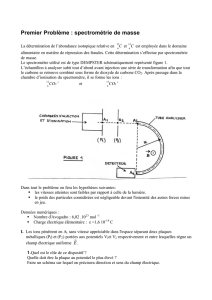
II. Spectrographe de masse de Dempster
1. • Dans un spectrographe de Dempster, on
accélère des ions Ne+ par une différence de poten-
tiel de 1000 V, puis on les soumet à un champ
magnétique de 0,1 T.
• Déterminer la position des impacts des deux
isotopes 20Ne et 22Ne sur la plaque photographique.
2. • En réalité, dans le faisceau initial après
accélération, il existe une incertitude Δv sur la vi-
tesse. Quelle incertitude maximum peut-on accepter
si on veut observer deux taches distinctes pour les
deux isotopes ?
Données : m(20Ne) = 19,99 u ; m(22Ne) = 21,99 u.
III. Expérience de J.J. Thomson
• Dans un tube cathodique contenant du néon
sous basse pression sont créés et accélérés des
ions Nen+.
• Le faisceau d'ions ainsi formé est soumis à
l'action simultanée d'un champ magnétique et d'un
champ électrique colinéaires, perpendiculaires à la
direction d'incidence des ions.
• On désigne par
!
v0
= v0
!
ux
la vitesse initiale
d'un ion de masse m et de charge q = n │qe│ ; on
désigne par L la distance parcourue selon Ox par
l'ion soumis aux champs électrique et magnétique.
1. • Déterminer les coordonnées y et z du point d'impact sur une plaque photographique placée perpen-
diculairement à Ox à la sortie du domaine où règnent les deux champs (on suppose que L ≪
!
mv0
qB
).
2. • Déterminer le lieu des points d'impact des ions ayant les mêmes caractéristiques, mais des vitesses
différentes (établir la relation z = z(y) en éliminant v0 entre y(x = L) et z(x = L) au point d'impact).

2
3. • Pourquoi cette expérience a-t-elle permis à J.J. Thomson de découvrir que le néon naturel est en fait
un mélange de deux isotopes 20Ne et 22Ne ?
IV. Systèmes d'équations couplées
• Une particule M (proton) de masse m et portant la charge électrique
positive q est mobile dans une région de l'espace (repérée par rapport à un
trièdre Oxyz orthonormé direct) où règnent :
◊ un champ électrique
!
E
uniforme de norme E et dirigé suivant Oz,
◊ un champ magnétique
!
B
uniforme de norme B et dirigé suivant Oy.
• La particule est émise sans vitesse initiale au point O à l'instant t = 0.
• La force de pesanteur est supposée négligeable.
• Pour simplifier les notations, on pose : ω =
!
qB
m
et R =
!
E
B"
.
1. a) Établir les équations différentielles vérifiées par les coordonnées (x, y, z) du point M en fonction du
temps t.
b) Que constate-t-on pour la coordonnée y ? Ceci était-il prévisible “géométriquement” d'après les
conditions de l'expérience ?
2. • Pour résoudre le système de deux équations couplées ((1) et (3)) concernant les coordonnées x et z,
on se propose d'utiliser une méthode par combinaison : on cherche s'il existe une variable u = α x + β z (où
α et β sont des constantes) telle que la combinaison correspondante des équations (α (1) + β (3)) puisse
s'écrire comme une équation faisant intervenir uniquement la variable u.
a) Justifier que, dans le cas particulier considéré, on peut pour cela simplifier les notations en impo-
sant α = 1.
b) Établir la relation que doit alors vérifier la constante β pour que la variable u ainsi définie possède
les propriétés souhaitées.
c) En déduire l'expression de u(t), puis la position (x, y, z) du point M en fonction du temps t.
d) Représenter sommairement la trajectoire.
Données : m = 1,67.10-27 kg ; q = 1,6.10-19 C ; E = 2.105 V.m-1 ; B = 0,5 T.
B. EXERCICE D'APPROFONDISSEMENT
V. Principe de relativité de Galilée
• Le principe “fondamental”
!
F
=
!
F
i
"
=
!
dp
dt
nʼest lié quʼà la variation de vitesse, et il sʼexprime de la
même manière dans deux référentiels galiléens, animés lʼun par rapport à lʼautre dʼun mouvement rectiligne
et uniforme (principe de relativité de Galilée).
◊ remarque : cela dépend des hypothèses associées au changement de référentiel pour une vitesse
d'entraînement
!
ve
; à partir de
!
OM
=
!
"
O M
+
!
ve
t et tʼ = t on déduit :
!
F
= m
!
OM
•• = m
!
"
O M
•• =
!
"
F
.
• Selon ce principe (pour un changement de référentiel galiléen), établir les relations entre les champs
électriques (
!
E
et
!
"
E
) et magnétiques (
!
B
et
!
"
B
) exprimés respectivement dans les deux référentiels R et Rʼ.