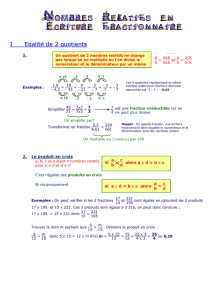
NOTES, nombres rationnels

Les nombres rationnels
[1]
1. Définition
Ce sont tous les nombres qui peuvent être exprimés comme le quotient de deux
nombres, en autres mots, une fraction. L’ensemble de ces nombres est dénoté par la
lettre . Ils peuvent être positifs ou négatifs.
Un nombre décimal qui peut être transformé en fraction est un nombre rationnel, mais
un qui ne peut pas ne l’est pas.
Exemple :
10
1
1,0 
donc 0,1 est un nombre rationnel
π = 3,14159265… n’est pas un nombre rationnel (il est un nombre irrationnel)
Exemples de nombres rationnels sont encerclés:
16
2
2. Les fractions impropres et nombres fractionnaires
Une fraction impropre est une fraction qui a une valeur qui est plus grande que 1 qui
est sous la forme
b
a
où a>b.
Exemple :
6
14
,
3
4
Un nombre fractionnaire est une fraction qui a une valeur qui est plus grande que 1
qui est sous la forme
c
b
a
.
Exemple :
3
1
2
9
4
10
On ne peut pas avoir une fraction impropre et fractionnaire en même temps.
On peut transformer une fraction impropre en nombre fractionnaire et vice versa.
Exemple :
3
1
2
peut être changé à
3
7
3
1
3
6
3
1
2
ou on utilise le raccourci :
3 x 2 + 1 = 7 et on met cette réponse sur le dénominateur original qui donne
3
7
Exemple :
De l’autre sens on divise 7 par 3. On peut mettre celui-ci 2 fois dans 7, donc notre
entier est 2. La fraction est le reste de la division sur le dénominateur original.
16
-3,18
25
74
4,5

Les nombres rationnels
[2]
3. Les fractions et les décimales
Une fraction et un nombre décimal sont deux façons d’écrire le même montant.
Exemple :
5,0
2
1
Ces deux chiffres veulent dire la même chose.
Pour transformer une fraction en décimale, on divise le numérateur par le
dénominateur. C’est pourquoi on écrit souvent une division sous forme de fraction.
Exemple : ⅝ → 5 ÷ 8 = 0,625
Pour transformer un nombre décimal en fraction, on observe jusqu’à quelle place
décimale est le chiffre. Le numérateur est les chiffres à la droite des zéros et le
dénominateur est la place décimale.
Exemple :
0,12  le chiffre se rend jusqu’au centième près, on ignore le premier zéro et on garde
le 12. La fraction est donc
100
12
.
0,024  le chiffre se rend jusqu’au millième près, on ignore les deux premiers zéros
et on garde 24. La fraction est
1000
24
.
4,9  le chiffre se rend jusqu’au dixième près, il n’y a pas de zéros à ignorer alors on
garde 49. La fraction est
10
49
.
4. Les fractions équivalentes
Une fraction est dite équivalente à une autre si ceux-ci représentent la même valeur.
Exemple :
6
3
4
2
2
1
Il faut faire attention aux signes négatifs.
5
2
52 5
2
On sait si on a une fraction équivalente si :
- leur nombre décimal est le même
- si on peut simplifier une fraction pour qu’elle devienne l’autre
Note : simplifier consiste à diviser le numérateur et le dénominateur par un
commun multiple.

Les nombres rationnels
[3]
5. Ordonner des nombres rationnels
Lorsqu’on veut ordonner des nombres, il est utile d’avoir toute la même forme
afin de comparer les nombres.
6. Additionner et soustraire des nombres rationnels
Si les dénominateurs sont pareils, on additionne les numérateurs et les dénominateurs
ne changent pas.
Exemple :
Si les dénominateurs sont différents, on trouve des fractions équivalentes de façon à
avoir des dénominateurs communs avant d’additionner.
Exemple :
7. Multiplier des nombres rationnels
On multiplie les numérateurs et on multiplie les dénominateurs.
Exemple :
8. Diviser des nombres rationnels
On prend la réciproque de la deuxième fraction et on multiplie.
Réciproque : on inverse le numérateur et le dénominateur.
Exemple :
9. L’ordre des opérations
On commence par faire toutes les multiplications et divisions. On fait les additions et
soustractions en deuxième.
PEDMAS – parenthèse, exposant, division, multiplication, addition, soustraction