TD : Diagrammes d`Ellingham

Elaboration des métaux 1
Diagrammes d’Ellingham
EdM11 Droite d’Ellingham Mg/MgO
Etablir la valeur de l’enthalpie libre d’oxydation du magnésium entre 300 et 1200 K.
Données : ΔfH°(MgO) = -601,7 kJ mol-1 ; S° = 32,7 ; 205 et 26,9 J mol-1K-1 respectivement pour Mgs, O2 et
MgOs. Le magnésium fond à 649°C et son enthalpie de fusion vaut Lf = 9,2 kJ.mol-1.
EdM12 Oxydoréduction
On considère les couples Cu/CuO, Al/Al2O3 et C/CO dont on donne les enthalpies libres standard des réactions
d’oxydation, soient :
ΔrG1°(T) = -314,8 + 0,186T (kJ mol-1)
ΔrG2°(T) = -1117,4 + 0,208T (kJ mol-1)
ΔrG3°(T) = -221,0 - 0,178T (kJ mol-1)
Tracer les diagrammes d’Ellingham et en déduire les réactions d’oxydoréduction possibles.
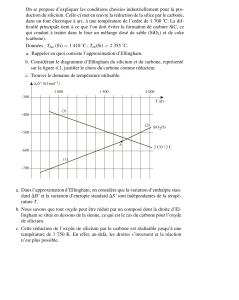
EdM13 Lecture d’un diagramme d’Ellingham
Le diagramme ci-contre rassemble les graphes
d’Ellingham des couples Al2O3/Al ; CO/C ; CaO/Ca ;
CuO/Cu ; MgO/Mg ; NiO/Ni ; V2O5/V ; ZnO/Zn.
1°) Ecrire les équations de formation de ces oxydes. En
déduire le graphe représentatif du couple CO/C.
2°) L’oxyde de cuivre oxyde tous les corps simples
considérés ; de même le calcium réduit tous les oxydes.
Identifier le graphe des couples CaO/Ca et CuO/Cu.
3°) Quelque soit la température, le vanadium réduit
l’oxyde zinc, mais pas l’oxyde de magnésium. La
réduction de l’oxyde de zinc par le nickel et celle de
l’oxyde de magnésium par l’aluminium n’interviennent
qu’à haute température. Identifier les graphes restant.
EdM14 Préparation d’un borure
Le tableau ci-dessous regroupe des grandeurs molaires standard du bore, du magnésium et de leurs oxydes
pour T = 298K.
espèce
ΔfH° (kJ.mol-1)
S°(J.K-1mol-1)
Tfus°(°C)
Δfus°(kJ.mol-1)
Tvap(°C)
Δvap°(kJ.mol-1)
O2(g)
0
205,0
55
-
90
-
B(s)
0
5,9
2313
15,9
2800
313,8
Mg(s)
0
32,7
923
9,2
1393
131,8
B2O3(s)
-1273
54,0
723
22,1
2520
230,1
MgO(s)
-601,5
27,0
3075
7,7
-
-
1°) Etablir dans les conditions d’Ellingham, les équations donnant les enthalpies libres d’oxydation ΔrG°(T)
de l’espèce réduite des couples B2O3/B et MgO/Mg ; tracer les graphes correspondants.
2°) Le borure de magnésium Mg3B2 s’obtient par action directe des deux corps simples en phase vapeur, l’un
provenant de la réduction de son oxyde par l’autre. Préciser les conditions d’obtention de ce borure en identifiant
l’oxyde à réduire.

EdM15 Diagramme d’Ellingham C/CO/CO2
Le concept de diagramme d’Ellingham est généralisable à tout couple Ox/Red mettant en jeu des espèces
associées l’une à l’autre par voie sèche par une quantité déterminée de dioxygène.
Pour le carbone et ses deux oxydes CO et CO2, on donne à 298 K (valeurs indépendantes de T) :
C(s)
CO(g)
O2(g)
CO2(g)
ΔfH°(kJ mol-1)
0
-110,5
0
-393,5
S°(J.K-1. mol-1)
5,7
197,6
205
213,6
1°) Commencer par étudier les deux couples CO/C et CO2/CO. Faut-il étudier le couple CO2/C ?
2°) Tracer le diagramme d’Ellingham du système carbone-oxydes de carbone et en déduire le domaine de
stabilité du monoxyde de carbone.
3°) On oxyde un excès de carbone par de l’air sous 1 bar. Quel oxyde de carbone obtient-on ?
4°) Pour l’équilibre H2 + 1/2O2 = H2O on donne ΔrG°(T) = -246200 + 55T (J.mol-1)
Préciser dans quel domaine de température l’oxydation du carbone par la vapeur d’eau conduit à la
formation de monoxyde, puis de dioxyde carbone.
Déterminer la nature des produits obtenus lorsque de la vapeur d’eau est projetée sur du carbone à 1200K.
Indiquer l’évolution du système lors d’une trempe à température ambiante.
5°) L’équilibre de conversion du monoxyde de carbone CO + H2O = H2 + CO2 joue un très grand rôle
dans le choix des réducteurs industriels. Déterminer le domaine d’utilisation de chacun d’eux.
EdM16 Diagramme d’Ellingham du fer
Les enthalpies libres standard de réaction décrivant l’obtention des divers oxydes de fer à partir d’une mole
de O2 et du fer s’expriment en fonction de T de la façon suivante :
FeO : ΔrG°1 = - 518 + 0,125T (kJ mol-1)
Fe3O4 : ΔrG°2 = - 545,1 + 0,156T (kJ mol-1)
Fe2O3 : ΔrG°3 = - 540,6 + 0,170T (kJ mol-1)
1°) Etablir les relations ΔrG°4(T), ΔrG°5(T) et ΔrG°6(T) relatives respectivement à l’oxydation de FeO en
Fe3O4 et Fe2O3 et de Fe3O4 en Fe2O3.
2°) Déterminer, à l’aide du tracé des courbes ΔrG°i(T), les domaines de stabilité de chacun ces oxydes de
fer.
EdM17 Réduction de la magnésie
La magnésie et l’oxyde de carbone sont très stables et ne subissent pas de transition de phase dans le
domaine de température considéré.
On considère les équilibres d’oxydation dont on donne les enthalpies standard de réaction :
2C + O2(g) = 2 CO : ΔrH1° = -221 kJ mol-1
900Κ<Τ<1393 Κ : 2Μg(l) + Ο2 = 2MgO : ΔrH2° = -1225 kJ mol-1
Τ>1393 Κ : 2Μg(g) + Ο2 = 2MgO : ΔrH3° = -1485 kJ mol-1
1°) A 1000K, les constantes d’équilibre des réactions 1 et 2 valent K°1 = 8.1020 et K°2 = 4.1051. Calculer
ΔrG1° et ΔrG2° à 1000 K. En déduire ΔrS1° et ΔrS2° à cette température. Exprimer alors ΔrG1°(T) et ΔrG2°(T).
2°) Etablir l’expression de ΔrG3°(T).
3°) Déterminer le domaine de température dans lequel le carbone réduit la magnésie.
EdM18 Réduction de la zincite
Au delà de la température d’ébullition du zinc (Tvap(Zn) = 1180K sous 1 bar), les couples rédox H2O/H2 et
ZnO/Zn sont décrits par les équations :
(1) 2 H2(g) + O2(g) = 2 H2O(g) : ΔrG1° = - 492 + 0,111T (kJ mol-1)
(2) 2 Ζn(g) + Ο2(g) = 2 ZnO(s) : ΔrG2° = -940 + 0,415T (kJ mol-1)
1°) Calculer la pression partielle du zinc en équilibre avec la zincite lorsqu’un excès de celle-ci est chauffé à T
= 1200K.
2°) La réduction de la zincite par le dihydrogène est décrite par l’équation-bilan :
(3) ZnO(s) + H2(g) = Zn(g) + H2O(g)

a) Calculer la température d’inversion de cet équilibre et préciser le domaine de température pour lequel la
zincite est réductible.
b) Déterminer la température T’ à laquelle il faut opérer pour que la constante de l’équilibre (3) soit égale à 15
3°) Un courant de H2 est envoyé sur de la zincite dans un four maintenu en permanence à la température T’ et
sous la pression totale 1bar. Déterminer les pressions partielles des diverses espèces gazeuses lorsque l’équilibre
(3) est réalisé.
4°) Une enceinte de volume V = 10,0L est placée dans le four à la température T’. Elle contient 2 moles de
dihydrogène et un excès de zincite.
a) Calculer la pression totale de l’enceinte lorsque l’équilibre (3) est réalisé.
b) Déterminer la masse minimale de zincite à introduire pour satisfaire l’équilibre.
EdM19 Chlorures de cuivre
L’oxydation du cuivre par le dichlore conduit à la formation des chlorures de cuivre (I) et (II).
Cl2(g)
Cu(s)
CuCl(s)
CuCl2(s)
ΔfH°(kJ mol-1)
0
0
-137,2
-220,1
S°(J.K-1.mol-1)
223,0
33,1
86,2
108,1
1°) Ecrire dans l’hypothèse d’Ellingham généralisée, les équations-bilans associant deux à deux Cu, CuCl
et CuCl2. Calculer la variance de chacun des systèmes.
2°) Etablir, pour les trois réactions ci-dessus, l’expression A(T,PCl2) de leur affinité en fonction de la
température et de la pression en dichlore.
3°) Tracer les courbes A°(T) correspondantes dans l’intervalle [25°C ; 400°C]. Préciser le sens physique
des divers domaines et droites du plan.
4°) Calculer les pressions de dichlore satisfaisant aux équilibres redox CuCl/Cu et CuCl2/CuCl, à 25 et à
400°C. En déduire, dans chaque cas, le résultat de l’oxydation du cuivre par un courant gazeux de dichlore à la
pression P° = 1bar.
5°) Du diclore circule, à θ = 80°C, sous une pression constante de 3.10-2 bar dans une canalisation en
cuivre. Indiquer si l’attaque du métal est possible et préciser dans l’affirmative le(s) produit(s) formé(s).
EdM110 Réduction du dioxyde de manganèse
Un certain nombre de réactions industrielles font appel au chlorure d’hydrogène. Les grandeurs molaires
standard utiles pour la suite sont regroupées dans le tableau ci-dessous :
espèce
O2(g)
H2O(g)
Cl2(g)
HCl(g)
Mn(s)
MnO2(s)
MnCl2(s)
ΔfH° (kJ.mol-1)
0
-241,8
0
-92,3
0
-522,1
-481,3
S°(J.K-1mol-1)
205
188,7
223,0
186,8
32,0
53,1
118,2
1°) Calculer, en fonction de la température, l’enthalpie libre standard de la réaction d’équation :
Mn(s) + Cl2(g) = MnCl2(s)
2°) Un diagramme, où les abscisses représentent la température T et les ordonnées la quantité y =
RTln(pCl2/P°) permet de définir 3 zones : y < ΔrG°(T), y = ΔrG°(T), et y > ΔrG°(T). Définir, pour chacune de ces
zones, la nature des systèmes chlore-manganèse pouvant exister.
3°) Le dichlore peut s’obtenir par réduction d’un oxyde de transition par le chlorure d’hydrogène. Dans le cas
de l’oxyde de manganèse (IV) MnO2, les deux réactions suivantes entrent en compétition :
(1) MnO2(s) + 2 HCl(g) = MnCl2(s) + H2O(g) + 1/2 O2(g)
(2) MnO2(s) + 4 HCl(g) = MnCl2(s) + 2 H2O(g) + Cl2(g)
a) Déterminer les enthalpies libres de réaction standard ΔrG1°(T) et ΔrG2°(T) des deux réactions et les
représenter graphiquement pour 400 < T < 1000K.
b) Préciser la variance de ces équilibres.
c) Discuter qualitativement, suivant le température, la possibilité d’obtenir du dichlore en enfermant dans un
réacteur MnO2 et le chlorure d’hydrogène.