1 Oscillateur harmonique (CORRIGES) 1. Mesure de masse en

Sup PCSI1 - Exercices de physique oscillateur harmonique (CORRIGES)
1
Oscillateur harmonique (CORRIGES)
1. Mesure de masse en apesanteur :
a) Système ; chaise, de masse m
o
représentée par un point matériel M de masse m
o
.
Actions : poids et rappel du ressort.
La RFD (ou deuxième loi de Newton) écrite en projection sur l’axe (Oz) donne : -m
o
g –k.∆L = m
o
.
(1)
où l’élongation algébrique du ressort est ∆L= z – L
o
, L
o
étant sa longueur à vide. Comme le poids de
la chaise va comprimer le ressort, on attend ∆L < 0, ce qui conduit à un terme de force de rappel
dirigé vers le haut, s’opposant au poids.
Il vient, après réaménagement de l’équation (1) :
soit formellement : 
Oscillations harmoniques de pulsation :
c’est à dire oscillations sinusoïdales, autour de la position d’équilibre z
éq
= L
o
– m
o
g/k.
Ces oscillations auront une période : 
ce qui conduit à : 
soit numériquement : m
o
= 25,1 kg.
b) En orbite, le poids est exactement compensé par la force centrifuge subie dans le référentiel lié au
satellite. Tout se passe comme si la pesanteur avait disparu (im-pesanteur).
On reprend une étude analogue, avec cette fois pour système l’ensemble {chaise + spationaute} de
masse m + m
o
.
L’équation du mouvement devient : –k.∆L = (m + m
o
).
soit avec toujours ∆L= z – L
o
: 
où cette fois : 
On tire donc : 
Soit numériquement : m = 58,2 kg. Le spationaute est probablement une spationaute...
M(m
o
)
g
z
z
z = 0

Sup PCSI1 - Exercices de physique oscillateur harmonique (CORRIGES)
2
2. Pendule élastique :
a. La position d’équilibre z
éq
de la masse m répond à 
avec ∆L = z - L
o
soit : mg – k(z – L
o
) = 0
dont la solution sera : z
éq
= L
o
+ mg/k.
b. L’équation du mouvement s’obtient par la projection de la RFD (ou
seconde loi de Newton) sur l’axe du mouvement, (Oz) :
soit : 
avec 
En posant : x = z – z
éq
, on aura 
et donc 
Solution générale : x(t) = A.cos(ω
o
t) + B.sin(ω
o
t)
Conditions initiales :
à l’instant initial la vitesse doit être  et le mobile est situé en sa position d’équilibre.
Soit x(0) = 0 et  .
Ceci amène A = 0 et  = Bω
o
donc B = -v
o
/ω
o
.
La solution x(t) s’écrit donc : x(t) = (-v
o
/ω
o
).sin(ω
o
t)
L’équation horaire z(t) en fonction de L
o
, m, g et v
o
sera finalement :
z(t) =(-v
o
/ω
o
).sin(ω
o
t) + L
o
+ mg/k.
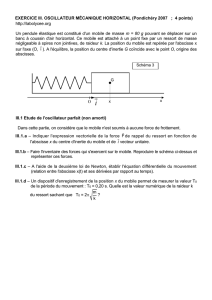
3. Exploitation d’un relevé expérimental.
a. amplitude : 2A = 6,0 cm donne A) 3,0 cm. T = 0,85 s donne une fréquence f = 1/T = 1,18 s et une
pulsation ω
o
= 2π/T = 7,39 rad.s
-1
; phase à l’origine : x(0) = 2,0 cm amène A.cosφ = x(0) dont on tire
φ = arccos(x(0)/A) cequi amène φ = ± 0,84 rad. Or φ > 0 car le signal est en avance de phase par
rapport à un signal de forme A.cos(ω
o
t) qui passerait par A en t = 0 (x(t) atteint A plus tôt).
-4
-3
-2
-1
0
1
2
3
4
0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6
x(t)
t (s)
x (cm)
2A
T
M(m)
g
z
z
z = 0

Sup PCSI1 - Exercices de physique oscillateur harmonique (CORRIGES)
3
b. A t = 0 , x(0) = 2,0 cm et v = dx/dt = -A.ω
o
.sinφ = -16,5 cm.s
-1
.
c. k = m.ω
o
² d’après l’expression de ω
o
(qu’on peut établir à partir de l’équation du mobile...).
k= 8,83 N.m
-1
.
d. Pour tracer l’allure des courbes v(t) et a(t) , s’appuyer sur la notion de courbe dérivée. v(t) est la
courbe présentant l’évolution de la pente du graphe x(t) et a(t) est la courbe présentant l’évolution
de la pente du graphe v(t). a(t) sera ici en opposition de phase vis à vis de x(t).
4. Masse percutant un ressort :
Système : masse m, qui glisse sans frottement le long de l’axe (Ox).
Référentiel : lié au support, galiléen.
Actions : poids, réaction du support (qui va exactement compenser le poids, dirigée verticalement),
rappel du ressort.
A t= 0, m prend contact avec le ressort, dont la longueur est alors à la longueur à vide, à la vitesse
constante   (avec v
o
> 0). Elle reste ensuite accrochée.
a. Ecrire l’équation du mouvement de la masse pour t > 0 :
Système : masse m, qui glisse sans frottement le long de l’axe (Ox).
Référentiel : lié au support, galiléen.
Actions : poids, réaction du support (qui va exactement compenser le poids, dirigée verticalement),
rappel du ressort.
A t= 0, m prend contact avec le ressort, dont la longueur est alors à la longueur à vide, à la vitesse
constante   (avec v
o
> 0). Elle reste ensuite accrochée.
Choisissons x= 0 en la position du point de contact O du ressort avec la masse m à t = 0. Ainsi,
l’élongation du ressort vaut ∆L = L – L
o
= x, et x sera négatif pour t > 0.
La force est dirigée selon (Ox), et sa projection sur cet axe est d’expression –kx. Cette force sera
ainsi bien dirigée vers la gauche de la figure quand le ressort est comprimé, pour x < 0.
La RFD donne sur (0x) :
La résolution générale amène :
x(t) = A.cos(ω
o
t) + B.sin(ω
o
t).
Les Conditions Initiales sont x(0) = 0 et donc A = 0 et v(0) = -v
o
donc comme v = -B.ω
o
.cos(ω
o
t) on
doit avoir : v(0) = -v
o
= -B.ω
o
.
Finalement : x(t)= (-v
o
/ω
o
).sin(ω
o
t).
b. La masse m vient percuter la paroi en une buttée B située à mi-distance de O et A si x atteint la
valeur –L
o
/2. Or lavaleur extrémale de x(t) sera (-v
o
/ω
o
).
On déduit la condition : v
o
> (L
o
/2).(k/m)
1/2
.
Retrouvons ce résultat par des considérations énergétiques.
x
x = 0
A
O

Sup PCSI1 - Exercices de physique oscillateur harmonique (CORRIGES)
4
Par la conservation de l’énergie mécanique, on a :
E
m
= (1/2)mv
o
² = cste. En toute position : E
m
= (1/2)mv² + (1/2)kx² avec E
c
= (1/2)mv² > 0.
La condition x atteint la valeur –L
o
/2 s’obtient pour x < -Lo/2, ce qui impose alors :
E
m
= (1/2)mv
o
² > (1/2)k(L
o
/2)² ce qui se traduit par v
o
> (L
o
/2).(k/m)
1/2
.
5. Reconnaître la forme canonique de l’équation de l’oscillateur harmonique :
1. l’équation du mouvement de l’aiguille, fournie, est :
avec θ faible donc sinθ ≈ θ , ceci amène:
Cette équation différentielle a la forme de celle d’un oscillateur harmonique ; on peut poser ω
o
² = M.B/J.
La fréquence des oscillations sera :
2. Pour le pendule simple : 
La conservation de l’énergie mécanique s’écrit : 
L’équation du mouvement du pendule est obtenue en décrivant l’expression précédente par
rapport au temps : 
soit après simplification, et compte tenu que pour θ faible on aura sinθ ≈ θ
On retrouve l’équation d’un oscillateur harmonique de pulsation propre ω
o
tlle que ω
o
² = g/L. la
période de ses oscillations sera : 
6. Oscillateurs à deux ressorts :
Appliquer la seconde loi de Newton, en analysant bien les actions exercées. Attention au sens des forces
de rappel des ressorts, à l’expression de la longueur des ressorts pour une abscisse x de M. Projeter le
résultat sur l’axe horizontal (Ox).
Situation 1 (ressorts de part et d’autre de M) :
soit : 
N.B. : On pourra vérifier que pour x = L
o1
, on a l’équilibre.

Sup PCSI1 - Exercices de physique oscillateur harmonique (CORRIGES)
5
La fréquence des oscillations sera : 
Situation 2 (ressorts reliés entre eux) :
Mouvement de M(m) : 
Mouvement de A (sans masse) :
ce qui amène :
En injectant ce résultat dans la première équation, on élimine ainsi y du problème :
N.B. : On pourra vérifier que pour x = L
o1
+ L
o2
, on a l’équilibre.
La fréquence des oscillations sera : 
7. Oscillateur symétrique à deux masses.
a) Au repos, le ressort est de longueur L= L
o
=10 cm. Tenu par le haut, la masse inférieure étant alors
suspendue, le ressort disposé verticalement s’allonge à une longueur de L = 12 cm.
Ecrivons la relation d’équilibre pour la masse située à l’extrémité inférieure du ressort ; celle-ci est
soumise à son poids et à la force de rappel élastique.
En projection sur la verticale, ceci conduit à l’équation :
mg – k.(L – L
o
) = 0 d’où k =mg/(L – L
o
) A.N. : k = 50 N.m
-1
.
Si le ressort est comprimé de façon à avoir une longueur de L’ = 8 cm, les masses étant immobiles et
disposées horizontalement, le système {masse 1, masse 2, ressort} à une énergie mécanique se limitant
alors à l’énergie potentielle élastique : E
m
= E
pél
= k(L’ – L
o
)²/2
b) Notons  et  les abscisses de chacune des masses ; L =  . Le système étant parfaitement
symétrique, les deux masses auront des déplacements opposés, et des vitesses opposées :
Ayant un système conservatif :
soit : 